4. Отсечение невыпуклым многоугольником.

Отсечение отрезка окном в форме невыпуклого многоугольника можно выполнить двумя способами.

1-ый способ.

Способ предполагает выполнение следующих действий.

1. Вводятся многоугольники, дополняющие заданный невыпуклый многоугольник до выпуклого.

2. Выполняется внутреннее отсечение полученным выпуклым многоугольником.

3. Далее для участка отрезка, полученного в результате этого внутреннего отсечения, осуществляется внешнее отсечение многоугольниками, дополняющими исходный до выпуклого. Полученная часть отрезка и будет видимой частью отрезка при его внутреннем отсечении заданным окном в форме невыпуклого многоугольника

Способ иллюстрируется ниже приведенным рисунком ().

Для окна, представленного на этом рисунке, дополняющим многоугольником будет треугольник СBD. Поэтому сначала выполняется внутреннее отсечение выпуклым многоугольником АBDE, в результате чего получается отрезок t₁t₃.Далее выполняется внешнее отсечение отрезка t₁t₃ треугольником СBD. В результате чего будет отброшена часть t₁t₂ , а оставшаяся часть t₂t₃ будет являться видимой частью исходного отрезка Т_нТ_к в заданном окне ABCDE.

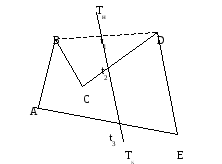
Рис. 3.4‑32

2-ой способ.

Способ предполагает выполнение следующих действий.

1. Заданный невыпуклый многоугольник разбивается на несколько выпуклых многоугольников.

2. Выполняется внутреннее отсечение заданного отреза всеми выпуклыми многоугольниками, составляющими исходнвъый не выпуклый многоугольник.

3. Отображение всех частей отрезков, полученных при выполнении пункта 2, позволит получить часть исходного отрезка, являющуюся результатом внутреннего отсечения исходного отрезка заданным невыпуклым многоугольником.

Наиболее удобным является разбиение исходного многоугольника на треугольники, которые всегда выпуклые. Эта процедура может быть выполнена следующим образом.

1. Определяются диагонали исходного многоугольника, соединяющие стороны его внутренних углов.

2. Из найденных диагоналей выбирается минимальная и соответствующий ей треугольник отбрасывается.

3. Далее процесс повторяется для оставшейся части многоугольника до тех пор, пока оставшаяся часть не станет треугольником.

Последний и отброшенные треугольники будут представлять собой множество треугольников, смоставляющих исходный многоугольник.

Для многоугольников, приведенного на следующем рисунке(Рис. 3.4 -33), отсечение треугольников будет выполняться в последовательности, соответствующей приведенной на рисунке нумерации диагоналей.

Рис. 3.4‑33

Достоинством данного способа является то, что нет необходимости проверять отдельные углы на выпуклость. Угол с минимальной диагональю, не звисимо от того, является ли исходный многоугольник выпуклым или нет, всегда будет не больше 180⁰.

4. Заливка областей.

Решение данной задачи обеспечивает придания всем внутренним точкам области, заданной своими границами, которые состоят из отдельных ребер, одинакового значение оптического параметра. В простейшем случае в результате заливки все внутренние точки рассматриваемой области приобретают один цвет (область как бы заливается чернилом заданного цвета).

При решении этой задачи для уменьшения количества обрабатываемых точек, целесообразно рассматривать только те точки пространства, которые находятся в габаритном прямоугольнике, построенном для заданной области (Рис.4-1).

В некоторых случаях существенного уменьшение количества обрабатываемых точек можно достигнуть, если габаритную фигуру для исходной области, представленной невыпуклым многоугольником, построить на основе габаритных прямоугольников отдельных выпуклых компонент заданной невыпуклой области, как это показано на приведенном рисунке (Рис.4-2Рис. 4.2 -36).

Рис.4-1.

На рисунке используются следующие обозначения:

• y1_max, y1_min, x1_max, x1_min – габаритные размеры первой выпуклой составляющей исходного невыпуклого многоугольника;

• y2_max, y2_min, x2_max, x2_min – габаритные размеры второй выпуклой составляющей исходного невыпуклого многоугольника.

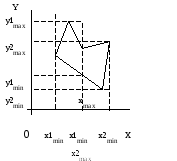
Рис.4-2.

Для решения задачи заливки области используются различные способы, к числу которых относятся:

• заливка с сортировкой;

• заливка по ребрам;

• заливка с использованием перегородки;

• заливка с затравкой.

• заливка с затравкой с использованием соседних групп.