3. Косоугольные проекции

Косоугольная проекция определяется углом наклона линии проецирования к плоскости проекции.

Отличие координат X,Y точки в исходной трехмерной системе и одноименных ее координат на плоскости проекции можно проанализировать на примере проекции единичного вектора по оси Z, которая приведена на Рис. 6.3 -62. На рисунке рассматривается случай, когда плоскость проекции совпадает с координатной плоскостью X,Y исходной трех мерной системы, из которой выполняется проецирование.

Рис. 6.3‑62

Проекцией конца единичного вектора, расположенного на оси Z (точки «т»), является точка на плоскости проекции, обозначенная как «тп», с координатами P_x и P_y. Эти координаты зависят от наклона линий проецирования, в частности от наклона линии проецирования, проходящей через конец рассматриваемого единичного вектора. С учетом этого, можно записать:

x_тп = x_т + Р_x = 0 + Р_x;

y_тп = y_т + Р_y = 0 + Р_x.

Величины Р_x и Р_y рассматриваются как отклонения, соответственно, по координатам X и Y при формировании косоугольной проекции точки.

Линии проецирования в рассматриваемой проекции параллельные, поэтому можно утверждать, что для всех точек исходной трех мерной системы с координатой по оси Z, равной «1», будет иметь место такие же отклонения по осям X и Y. Кроме того, очевидно при изменении координаты Z будут пропорционально изменяться отклонения по осям X и Y. Это позволяет записать для любой точки A(x_A, y_A, z_A) исходной трех мерной системы ее координаты на плоскости проекции как:

x_Aп = x_A + Р_x z _A;

x_Aп = y_A + Р_y z _A.

Матрица, отражающая эту связь координат, имеет вид:

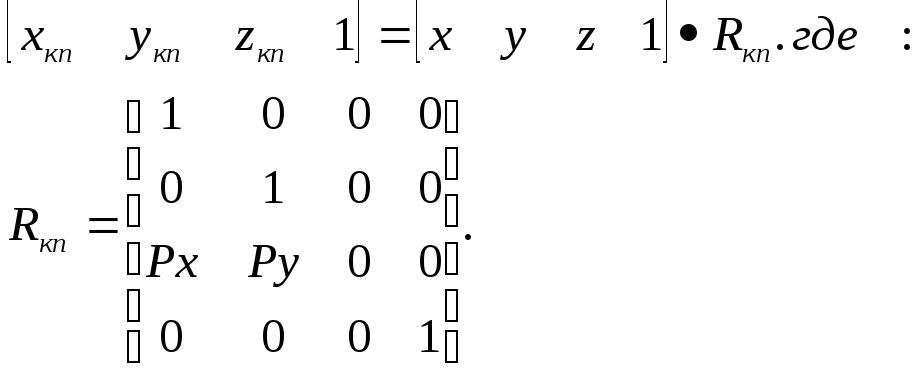
Для свободной косоугольной проекции имеет место:

Р_x = сos 45⁰;

Р_y = sin 45⁰.

Для кабинетной косоугольной проекии используется уменьшенный масштаб влияния координаты Z на смещение:

Р_x = 0.5 сos 45⁰;

Р_y = 0.5 sin 45⁰.

4. Аксонометрическая проекция

Простейшим случаем аксонометрической проекции является ортогональная проекция. Это такая аксонометрическая проекция, у которой плоскость проекции перпендикулярна одной из координатных осей исходной трех мерной системы координат. При этом возможны три случая.

Первый случай.

Плоскость проекции перпендикулярна оси Z и совпадает с координатной плоскостью XY. Проекция точки в этом случае определяется как:

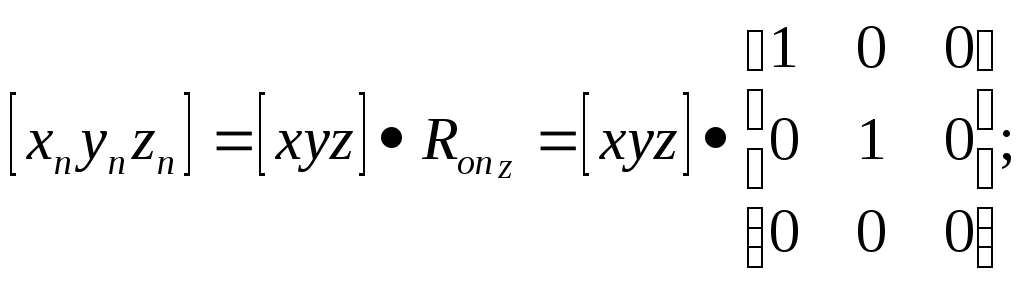
Второй случай.

Плоскость проекции перпендикулярна оси X и совпадает с координатной плоскостью ZY. Проекция точки в этом случае определяется как:

Третий случай.

Плоскость проекции перпендикулярна оси Y и совпадает с координатной плоскостью XZ. Проекция точки в этом случае определяется как:

Общий случай аксонометрической проекции, когда плоскость проекции занимает произвольное положение в исходной трех мерной системе координат, иллюстрируется ниже приведенным рисунком (Рис. 6.4 -63).

Рис. 6.4‑63

На рисунке приведены следующие обозначения:

• ПП – плоскость проецирования;

• V – вектор направленности линий проецирования;

• b – угол между осью Z и проекции вектора V на координатную плоскость XZ;

• a – угол наклона вектора V к координатной плоскости XZ.

Найдем матрицу аксонометрической проекции R_пп, которая связывает координаты x, y, z точки в трех мерной системе и ее координаты x_п, y_п, z_п на плоскости проекции ПП (координата z_п на плоскости проекции равна 0):

Матицу R_пп можно найти, выполнив два этапа преобразований.

Первый этап.

От исходной системы координат перейдем в видовую систему координат, направление оси Z_в которой совпадает с вектором проецирования V. Для этого исходную систему координат повернем на угол «в» относительно оси Y, а полученную систему координат повернем на угол «a» относительно оси X. Тогда матрица видового преобразования R_в рассчитывается следующим образом:

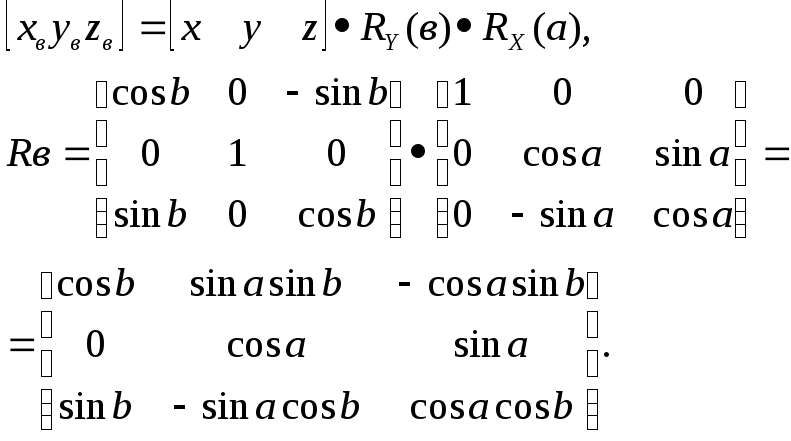
Полученная матрица обеспечивает переход к видовой системе координат, ось Z которой перпендикулярна плоскости проекции. Для такой видовой системы координат заданная проекция превращается в ортогональную проекцию с плоскостью проекции, перпендикулярной оси Z. Поэтому для получения матрицы аксонометрической проекции R_пп необходимо матрицу R_в умножить на матрицу R_опz ортогональной проекции на плоскость X,Y,0, т.е. имеем:

Полученная матрица обеспечивает преобразование для общего случая аксонометрической проекции, называемой триометрией, при которой углы «a» и «в» выбираются независимо друг от друга.

Для вывода зависимостей параметров аксонометрии для случаев диметрии и изометрии, рассмотрим аксонометрические проекции единичных векторов по координатным осям:

Используя матрицу аксонометрической проекции, запишем проекции этих векторов:

Возьмем диметрию, у которой координатные оси X и Y имеют одинаковые углы с осью Z. В этом случае можно утверждать, что проекции единичных векторов U_x и U_y , будут иметь одинаковую длину, а следовательно можно записать:

U_xп² = U_уп², т. е.

cos²b + sin²a sin²b = cos²a.

Разрешим это уравнение относительно «b», используя только функцию sin:

1-sin²b + sin²a sin²b =1- sin²a;

(6.4-1)

Таким образом, при построении диметрии, задавая произвольный угол «а», необходимо по полченной формуле рассчитать угол «b».

Для изометрии проекции всех рассматриваемых единичных векторов будут одинаковыми. Поэтому можно записать:

U_zп² = U_уп², т. е.

sin²b + sin²a cos²b = cos²a.

Разрешим это уравнение относительно «b», используя только функцию sin:

sin²b + sin²a (1-sin²b) = 1-sin²a,

(6.4-2)

На основании выражений (6.4-1) и (6.4-2), можем записать:

sin²a = 1- 2sin²a, откуда:

sin²a = 1/3, а .

Подставляя полученное значение для sin a в выражение (6.4-1), будем иметь:

Из этого следует, что для задания изометрии, необходимо взять в качестве значений для ее параметров «а» и «в» выше рассчитанные значения.