
Презентации и конспект лекции Синицын / Презентации_ВЭиМОвТС / ВычЭксперим / Лекция8_Финитные функции
.pdfТема 8. Финитные функции и аппроксимация
Базис из финитных функций
Теория Стренга-Фикса аппроксимации финитными функциями
В-сплайн и некоторые наиболее часто используемые базисы
Двумерные финитные функции на треугольной сетке
05.01.2011 |
1 |

Базис из финитных функций
Финитной называется функция |
k |
( x ) , определенная для всех |
|
|
|
|
|
• |
x ( ) , но отличная от нуля лишь на некоторой |
||
|
конечной области k , называемой конечным носителем |
||
|
|
0, |
x |
k |
, |
k |
( x ) |
|
|
|
|
|
x k . |
||||
|
( x ), |
||||
1 |
|
|
0 

1
05.01.2011 |
2 |
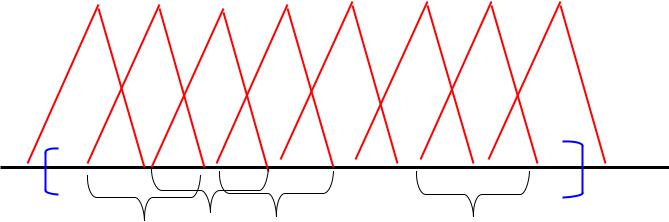
Построение базиса
Область разбивается на конечные элементы,
на каждом из которых определена финитная функция
2 |
3 |
|
|
|
|
|
|||
|
|
|
4 |
k |
|
|
|
|
a |
2 |
3 |
4 |
b |
|
k |
05.01.2011 |
3 |
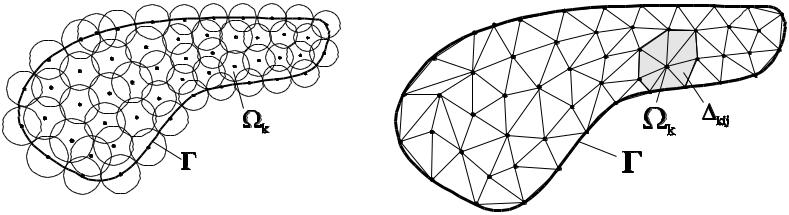
Построение базиса
N |
|
|
|
|
k ; |
k |
; |
k i k |
и л и i . |
k 1 |
|
|
|
|
05.01.2011 |
4 |
Хорошие свойства базиса из финитных функций
1. Ввиду квазиортогональности
k , i k i d |
|
k |
|
0; |
k |
i |
0 |
i d |
0; |
k |
i |
0 |
|||
|
k i |
|
|
||||
|
|
|
|
|
|
матрица проекционного уравнения сильно разрежена. Более того, если условие k i выполняется только для смежных носителей, то матрица получается ленточной.
2. Возможность выбора специфических приграничных конечных элементов и связанных с ними финитных функций, учитывающих особенности границы, позволяет эффективно решать краевые задачи на достаточно произвольной области.
05.01.2011 |
5 |
Представление искомой функции
При таком выборе базиса естественно поставить вопросы о его полноте, выборе вида функций и аппроксимационных свойствах разложения искомого решения в виде
N
u ~ u N ( x ) a k k ( x )
k 1
На эти вопросы частично отвечает Теория Стренга-Фикса аппроксимации финитными функциями
05.01.2011 |
6 |
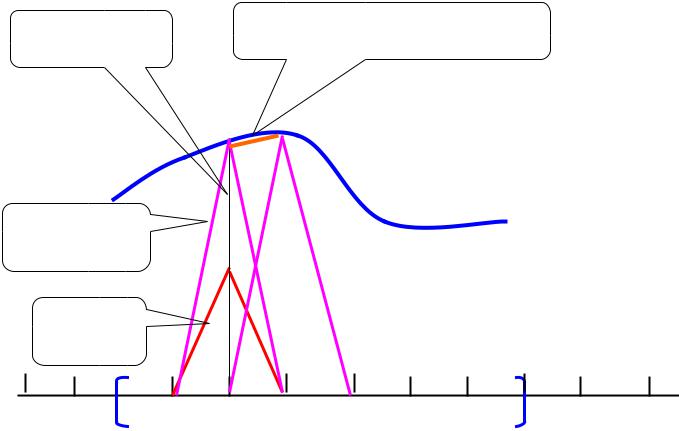
a =u(x ) |
ak k(x)+ ak+1 k+1(x) |
|
k |
k |
|
u(x)
ak k(x)
k(x)
0 |
xk |
xk+1 |
b |
|
|
05.01.2011 |
7 |
Теория Стренга-Фикса аппроксимации финитными функциями
Изложим основные идеи этой теории для функций одной переменной с регулярными конечными элементами
Область |
|
0, b |
покрываем равномерной сеткой: |
|
||
|
|
|
|
|
||
x k |
k p h , |
h b / n , |
k 1 ... N ; |
N n 1 2 ( p 1); |
p 1, 2 , ... |
|
|
|
|
p=1 |
p=2 |
|
|
x1 p=1
|
xk |
xi |
b |
x1 p=2 |
0 |
|
|
|
|
|
05.01.2011 |
8 |
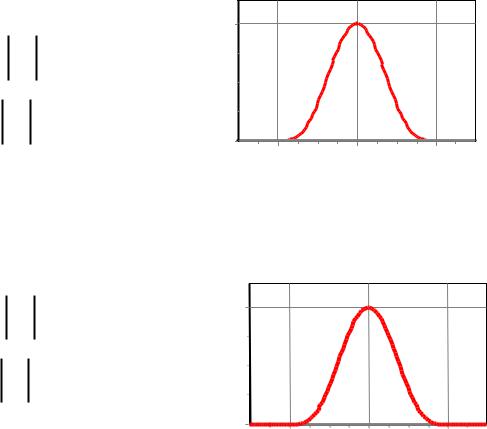
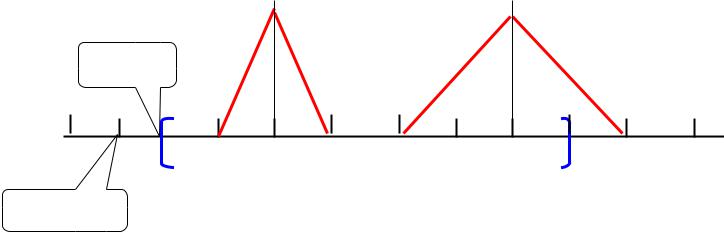
Нормированные финитные функции
0,
p ( x )
( x ),
0 ,
1 ( x )
( x ),
xp ,
xp .
x1,
x1 .
1 |
p |
|
0 |
|
|
-1 |
0 |
1 |
-p |
|
p |
1 |
1 |
|
0 |
|
|
-1 |
0 |
1 |
-1 |
|
1 |
05.01.2011 |
9 |
Базисные Финитные функции
Конечные элементы:
k xk ph , xk ph
Базисные финитные функции = сдвиги стандартной финитной ф-ии
p |
|
p |
x k p h |
|
p x x k |
|
|
1 |
x x k |
|
||||
k |
( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
h |
|
p h |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
05.01.2011 |
10 |
