Билет 12.

Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.

Интеграл вида f(t)dt=Ф(x), x[a,b] – интеграл с перем. верхним пределом.

Теорема 1: пусть f(x) непрерыв. на [a,b], тогда Ф(х)=f(t)dt тоже непрерыв. на [a,b]

Док-во: х[a,b] возьмем (х+х) [a,b]. Рассмотрим Ф(х)=Ф(х+х)-Ф(х)= f(t)dt-f(t)dt=f(t)dt+f(t)dt-f(t)dt=f(t)dt=f()х, где [х, х+х].

Ф(х)=f()х.

х0 => Ф(х)0, что означает непрерывность Ф(х) в точке х.

т.к. х – любое, то Ф(х) непрерыв. на [a,b]. ч.т.д.

Теорема 2 (т. Барроу):пусть f(x) непрер. на [a,b], тогда Ф(х)=f(t)dt явл. первообразной для f(x) на [a,b], т.е. (f(t)dt)=f(x)

Производная от интеграла с перем. верхним пределом равна подинтегр. ф-ции от перем. предела.

Док-во: Ф(х)=f()х, где [х, х+х]

(f(t)dt)=Ф (x)=lim_х0 Ф(х)/ х= lim_х0 f()х/х= lim_х0 f() (тогда х) =f(x) ч.т.д

f(х)dх=f(t)dt+С

Пусть F(x) – некот. первообразная для f(x)

Ф(х)=F(х)+С₀

f(t)dt=0

0=Ф(a)=F(а)+С₀ => С₀ = -F(а) => Ф(х)=F(х)-F(а)

Ф(b)=F(b)-F(а)

f(х)dх=F(b)-F(а) – ф-ла Ньютона-Лейбница

Вывод: если f(х) непрер. на [a,b], то для любой ее первообразной F(х) на [a,b] имеет место ф-ла Н.-Л.

Билет 13.

Замена переменных в определенном интеграле.

Теорема 1 (внесение множителя под знак дифференциала): Пусть u=(x) непрер. дифференцируема на пром-ке с концами a и b; пусть f(u) непрер. на множ-ве значений u=(x) Е().

Тогда f((x)) (х)dx=f(u)du

Док-во: если f(u) имеет первообр. F(u), то f((x)) (х) имеет первообр. F( (x))

f((x)) (х)dx= F( (x)) |^b_a= F( (b)) - F( (a)); f(u)du=F(u) |^(b)_(a)= F( (b)) - F( (a)) ч.т.д.

Теорема 2 (вынесение множителя из-под знака диф-ла): Пусть х=(t) непрер. диф-ма на (,); (t)>0 (=> возрастает) ((t)<0); ()=a; ()=b; пусть f(x) непрер. на пром-ке с концами a и b, тогда

f(х)dх=f((t)) (t)dt

Док-во: g(t)= f((t)) (t); если g(t) имеет первообр. G(t) на (a,b), то f(x) имеет первообр. F(x)=G(^-1(x)) (сущ-ние ^-1(x) гарантировано монотонностью: ^-1(x)>0 (<0)); f((t)) (t)dt= G(t) |^_=G() – G()

f(х)dх=G(^-1(x)) |^b_a=G(^-1(b)) - G(^-1(a))= G() - G() ч.т.д.

Билет 10

Понятие определенного интеграла и его геометрический смысл. Ограниченность интегрируемой функции. Основные классы интегрируемые функции.

y=f(t), кот определ на [a,b].

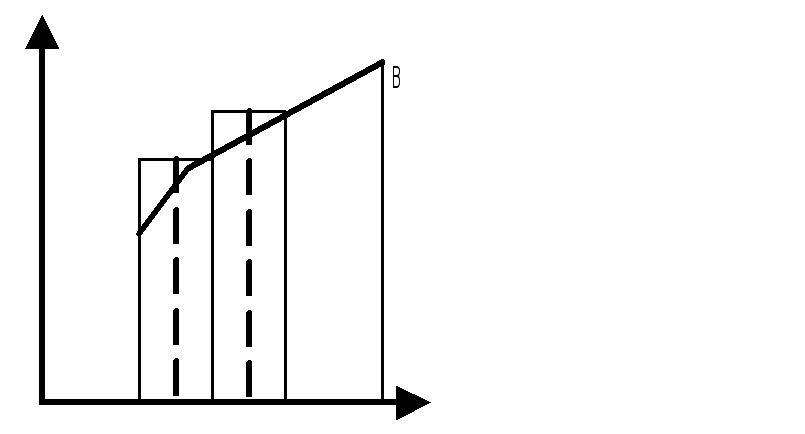
а<b, τ_n={x₀, x₁, x₂,..,x_n |a=x₀<x_1...<x_n=b|}

Δx_k=x_k-x_k-1-длина отр.[x_k-1,x_k], к=1,n.

λ=max ∆x_k – диаметр разбиения 1≤k≤n

k€ [x_k-1,x_k], k=1,n,

σ_n=f(ε₁)Δx₁+ f(ε₂)Δx₂+..+f(ε_n)Δx_n=∑f(ε_k)Δx_k Интегральн.сумма.

Опр:если сущ. конечн.предел инег.суммы Р, при λ→0 независящ. от способа разбиения τ_n [a,b] и выбора промежуточных точек ε_k то этот предел – опред.интеграл (Р) на [а,b] от y=f(x).

Е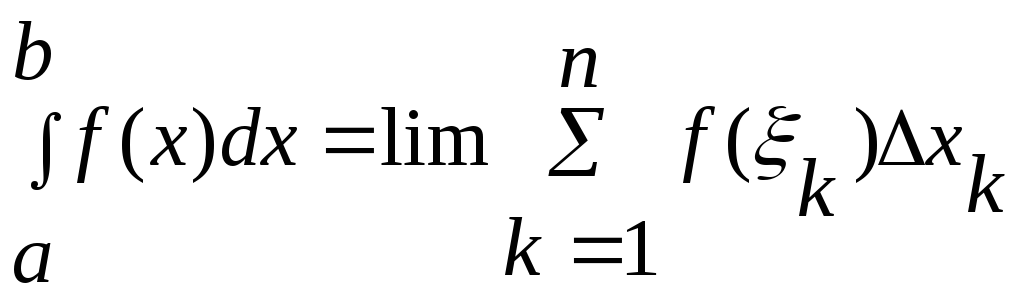 сли этот lim сущ, то y=f(x) интегрируемая по Риману на [a,b].

R[a,b]- класс всех ф-ций интегр. на [a,b].

Опр. интег.-это число; неопр.интег.-совокупность всех первообразных.

Геометр. смысл ОИ. y=f(x) неприрывна на [a,b]. f(x)≥0.

A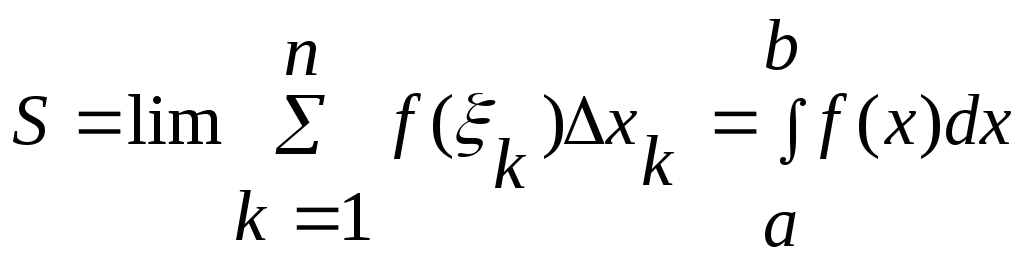 B; x=a; x=b; [a,b] –криволин.интегр.

Ограниченность ∫-ой ф-ции.

1.(необход.условие ∫-ти ф-ции). Если y=f(x) ∫-ма по Риману то она ограничена. f(x) € R[a,b] →сущ.М>0, |f(x)|≤M, для любых х€[a,b].

Д-во: предположим, что f(x) не огран. на [a,b] тогда при люб. разбиении τ_n найдется часть от k [x_k-1,x_k] на котором f(x) не ограничена. В этом случае можно выбрать ε_k€[x_k-1,x_k], таким обр, чтобы |f(ε_k)|>любого наперед заданного положит. числа, а это означ., что не сущ-ет конечного lim_x→0 _n

Следствия: если ф-ция неогр. то на неинтегрируема на [a,b]; огранниченность явл. лишь необход. условием инт-сти, но не достаточным.

 1, х – рацион.

D(x)=  0, х – иррац.

D(x) – огр. на [0,1]

ε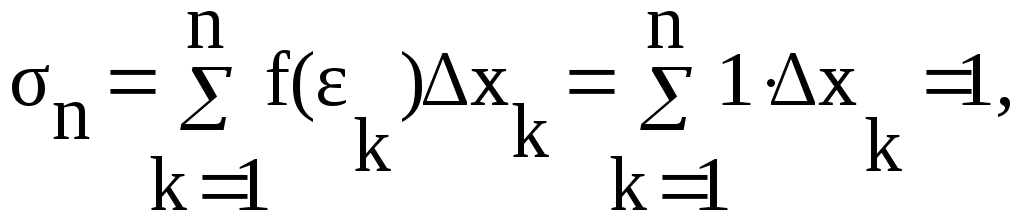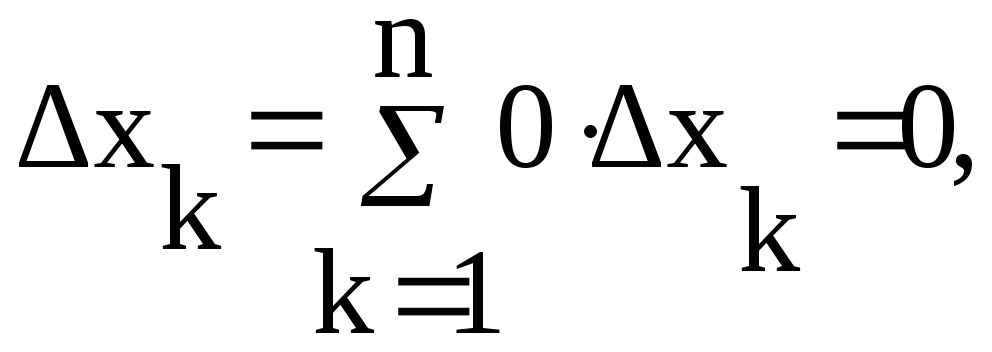_k-рац.

ε_k-ирррац

D(x) – не инт. по Р., но она огр.

Теорема 1: f(x) непр. [a,b], то она явл. интегр.

Теорема 2: f(x) кусочно-непрер. на [a,b]

Ф-ция f(x) явл. кусочно-непрер. на [a,b], если она огранич. и непрер. на отр. [a,b] всюду, кроме конечн. числа точек разрыва 1-го рода.

Теорема 3: Ф-ция f(x) монотонная на [a,b] интегр. на [a,b] …

Билет 11

Св-ва опред. ин-ла.

1. f(х)dх=0

2. dх=b – a; f(x)1

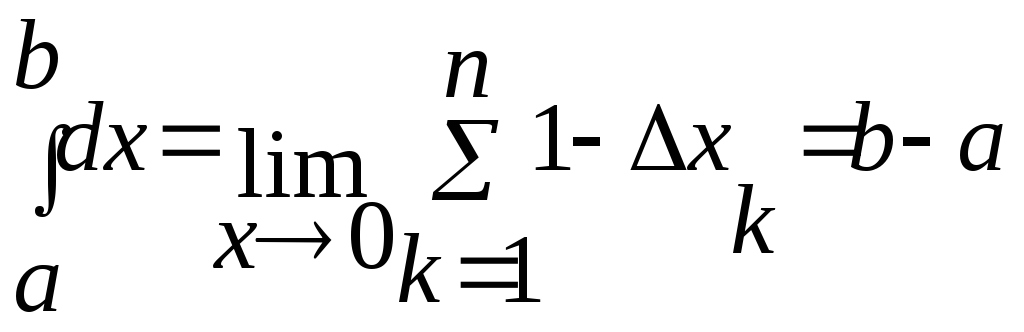
3. f(х)dх= - f(х)dх

4. f(x)R [a,b]; C f(х)dх=C f(х)dх=

=

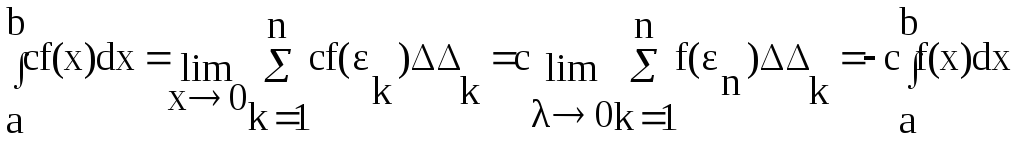
5. f(x), g(x)  R [a,b], то f(x)+g(x)  R [a,b]; (f(х)+g(x))dх=f(х)dх+g(х)dх

6. (аддитивность опред. ин-ла)

 a, b, c f(х)dх=f(х)dх+f(х)dх

7. Если f(xх[a,b], то f(х)dх0, a>b f(х)dх=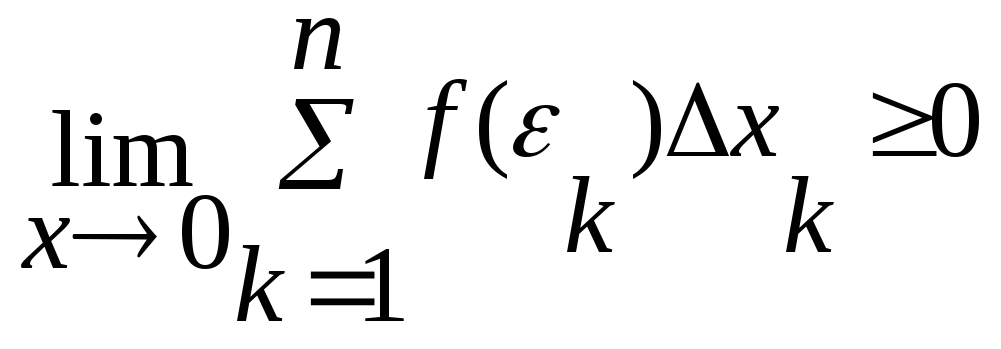

8. Монотонность опред. инт.: Если f(x), g(x)R [a,b], f(x)g(x) x[a,b], то f(х)dх<g(х)dх, a<b

Док-во: g(x) – f(x)0 x[a,b], 0(g(x) – f(x))dx=g(х)dх - f(х)dх

9. Если f(x)R [a,b], то |f(x)|R [a,b]

|f(х)dх ||f(х)|dх

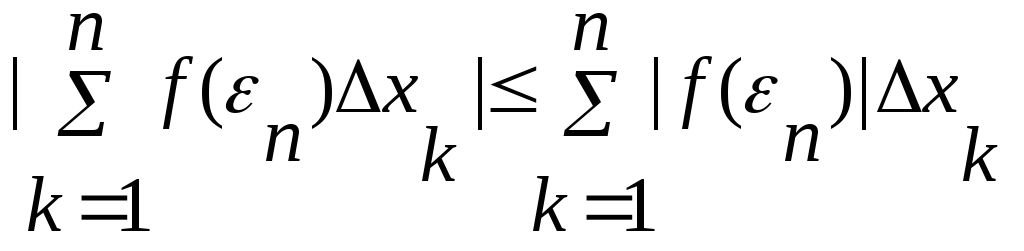
10. (Оценки опред. инт.): Если m и M – наимен. и наибол. зн. f(x) на [a,b], то m(b-a) f(х)dхM(b-a)

mf(x)M; x[a,b]

mdх f(х)dхMdх

m(b-a)f(х)dхM(b-a), a<b

11. Теорема о среднем: Если f(x) непр. на [a,b], то  т. [a,b], что выполн. рав-во f(х)dх=f()(b-a)

Док-во: f(x) непр. на [a,b], m – min зн. f(x) на [a,b], M – max; x[a,b] mf(x)M; иссл. оценку ин-ла:

m(b-a)f(х)dхM(b-a), b-a>0

: (b-a) m(f(х)dх) / (b-a))M; ::=f(х)dх) / (b-a)

найдется такая , что f()=,[a,b] => f(х)dх=f()(b-a) ч.т.д.

Билет 6.

Интегрирование по частям в неопределённом интеграле.

Т. Пусть функции U(x) и V(x) непрерывны на некотором промежутке X, дифферинциируемы в его внутренних точках и на Х существует , тогда

На Х существует , причем = u(x)v(x)- , или

;

Док-во:

d(uv)=vdu+udv;

Билет Интегрирование рациональных функций.

Интеграл от многочлена – легко и просто. Правильная рациональная дробь раскладывается на сумму элементарных дробей.

Типы дробей:

1), 2),3) ,4)

1)

2)

3)

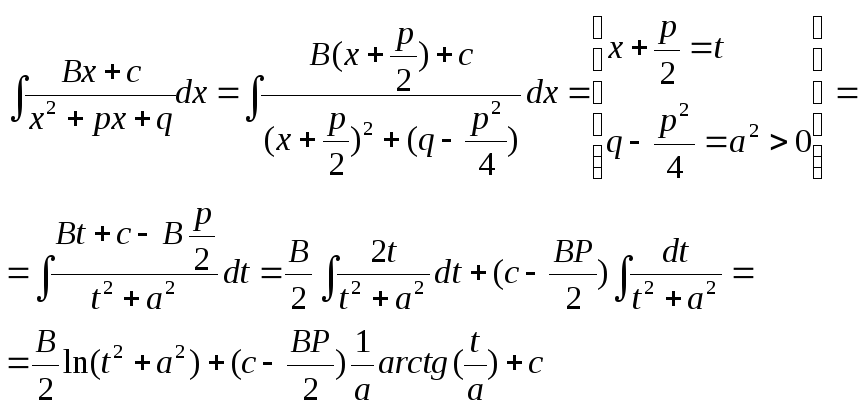
4)

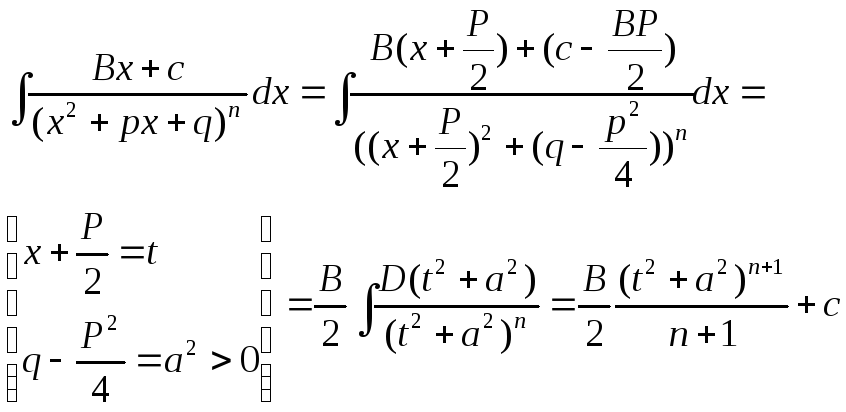
- рекуррентная формула

Вывод: интеграл от любой рациональной ф-ции выражается элементарной ф-цией ln,arctg, степенная.

Билет 37.

КРИ-2

Механический смысл КРИ-2:

(М) – вектор силы; L=AB; Работа силы по перемещению вдоль L. Если (М) – переменная сила, а AB – кривая, то: - настолько малы, что перемещение на кусочек по направлению совпадает с единичным касательным вектором. -произвольная точка.() – постоянная сила. =((),)=((),)

!!! С механической точки зрения КРИ-2 представляет собой работу силы вдоль линии L.