
Билет 43.
Векторные поля и их основные характеристики.
Говорят, что в V занадо
векторное поле, если каждой т.
![]() поставлен
в соответствие некоторый вектор
поставлен
в соответствие некоторый вектор![]() .
Физ. Векторные поля не зависят от выбора
СК.
.
Физ. Векторные поля не зависят от выбора
СК.
![]()
Векторная линия – кривая, в каждой точке
M которой
![]() направлен по касательной к кривой.
Векторная трубка – часть пространства,
состоящая из целых векторных линий,
каждая ВЛ или целиком лежит внутри этой
трубки или находится вне ее.
направлен по касательной к кривой.
Векторная трубка – часть пространства,
состоящая из целых векторных линий,
каждая ВЛ или целиком лежит внутри этой
трубки или находится вне ее.
Поток векторного поля. Дивергенция.
![]()
Дивиргенцией векторного поля
![]() называется
скалярная ф-ция
называется
скалярная ф-ция
![]() .
.
Формула Остроградского:
![]()
![]() характеризует плотность источников
поля в данной точке. Не зависит от выбора
СК.
характеризует плотность источников
поля в данной точке. Не зависит от выбора
СК.
Циркуляция и ротор векторного поля.
Ротором (или вихрем) векторного поля
![]() называется вектор-функция
называется вектор-функция

Ротор характеризует завихренность поля в данной точке.
Ротор является постоянным вектором, направленным вдоль оси вращения OZ. Его модуль равен удвоенной угловой скорости вращения тела.
Рассмотрим
![]() .
С- кусочно гладкая пов-ть. КРИ-2
.
С- кусочно гладкая пов-ть. КРИ-2
![]() называется циркуляцией
называется циркуляцией
![]() вдоль кривой L в направлении
вдоль кривой L в направлении
![]() .
Если
.
Если
![]() -силовое
поле, то его циркуляция – работа вдоль
пути L.
-силовое
поле, то его циркуляция – работа вдоль
пути L.
![]()
(формула Стокса).
Билет 44.
Специальные виды векторных полей.
Потенциальное векторное поле.
![]() называется потенциальным в области G,
если его можно представить как градиент
некоторого скалярного поля U(M).
называется потенциальным в области G,
если его можно представить как градиент
некоторого скалярного поля U(M).
![]() Функция U(M) – потенциал
векторного поля
Функция U(M) – потенциал
векторного поля
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Т.о. в потенциальной поверхностно
односвязной области G
поле
![]() обладает
следубщими свойствами:
обладает
следубщими свойствами:
1) циркуляция потенциального
![]() вдоль
любого замкнутого контура равна нулю.
вдоль
любого замкнутого контура равна нулю.
![]()
2) Для любых т. А,В из области G
циркуляция потенциального поля
![]() не зависит от выбора кривой АВ, а зависит
только от выбора А и В.
не зависит от выбора кривой АВ, а зависит
только от выбора А и В.
![]()
3) Потенциальное поле
![]() является
безвихревым
является
безвихревым
![]()
![]() - необходимое и достаточное условие
потенциальности поля
- необходимое и достаточное условие
потенциальности поля
![]() в поверхностно односвязной области.
в поверхностно односвязной области.
Сопеноидальное векторное поле.
Векторное поле
![]() называется сопеноидальным в области
G, если в этой области
называется сопеноидальным в области
G, если в этой области
![]() (нет
источников).
(нет
источников).
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Закон сохранения интенсивности векторной трубки в сопеноидальном поле.
В сопеноидальном поле
![]() поток через любое сечение векторной
трубки имеет одно и тоже значение.
Векторные линии в соп. поле не могут
начинаться или заканчиваться внутри
областисопеноидальности.
поток через любое сечение векторной
трубки имеет одно и тоже значение.
Векторные линии в соп. поле не могут
начинаться или заканчиваться внутри
областисопеноидальности.
![]() -это
поле является соп-м.
-это
поле является соп-м.
Любое физ векторное поле C
может быть представлено в виде суммы
![]() и
и
![]() ,
где
,
где
![]() -потенциальное,
-потенциальное,
![]() -соленоидальное.
-соленоидальное.
Гармоническое векторное поле.
![]() гармоноческое,
если оно является одновременно
потенциальным и сопеноидальным.
гармоноческое,
если оно является одновременно
потенциальным и сопеноидальным.
 ;
;
![]()
![]() ;
;
![]()
Билет 21.
Частные производные и их геометрический смысл.
Частная производная ф-ции
![]() в
точке
в
точке
![]() по
переменной x называется
по
переменной x называется
![]() ,
если он
,
если он
![]() .
.
![]() ;
;
![]() ;
;
![]() непрерывна
непрерывна
![]()
![]() имеет частные производные в т. А,В
имеет частные производные в т. А,В
![]() непрерывна
в т. А,В.
непрерывна
в т. А,В.
Билет 14.
Интегралы от периодических, нечетных и четных ф-ций.
Теорема: Пусть f(x)
интегр. на [-a,a],
тогда если f(x)
четная, то
![]() ,
если нечетная, то
,
если нечетная, то
![]() .
.
![]()
Если f(x) – непрерывная с периодом T, интегрируемая на некотором отрезке длины Т, то она интегрируема на любом отрезке длины Т.
![]()
![]()
Док-во:
![]()

![]()
Интегрирование по частям в определенном интеграле.
![]() -
непр. диф-е ф-ции на
-
непр. диф-е ф-ции на
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Билет 32.
Двойной интеграл, его вычисление в декартовой прямоугольной системе координат.
![]() ;
;
![]() ;
;
y-трапецевидная область
Д.
![]()
x-трапецевидная область
Д
![]()
Пусть в основании цилиндрического тела лежит y-трапецевидная область.
![]() ;
;
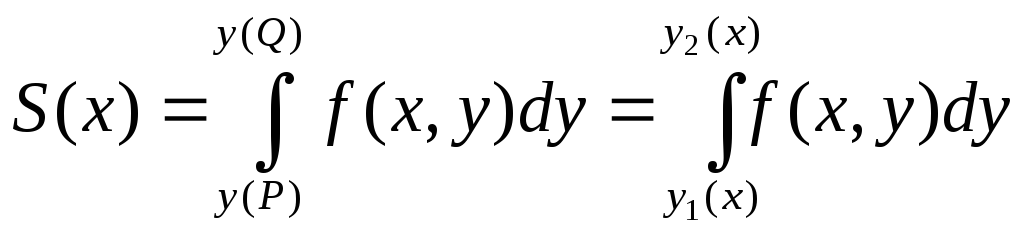 ;
;
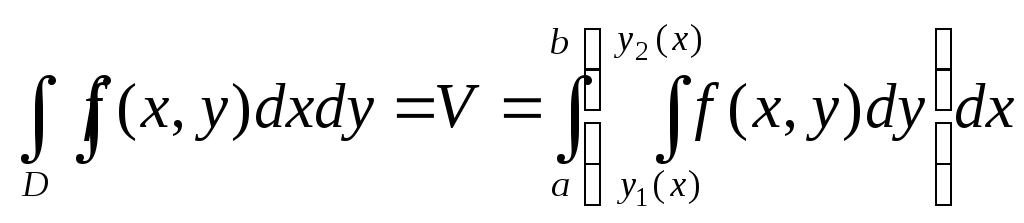
 для y-трапецевидной
области
для y-трапецевидной
области
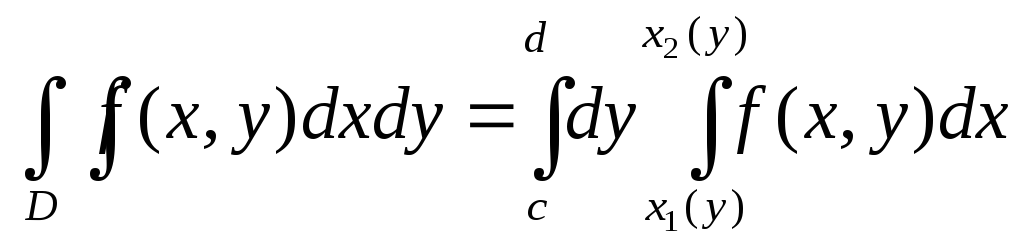 для x-трапецевидной
области
для x-трапецевидной
области
Замечание: области более сложного вида разбиваются на сумму трапецевидных областей.
Билет 25
Частные производные и дифференциалы функции нескольких переменных.
-
z=f(x,y); f x(x,y), f x(x,y)
d/dx*(df(x,y)/dx)=d2f(x,y)/dx2=(f x(x,y))x=f xx(x,y)= f x2= d2z/dx2=z x2
d/dy*(df(x,y)/dx)=d2f(x,y)/(dx*dy)=(f x(x,y))y=f xy= d2z/(dx*dy)=z xy
d/dy*(df/dy)=d2f /d2y2=f y2=d2z /dy2=z y2
В общем случае частные производные зависят от порядка дифф.
Теорема: Пусть ф-ция z=f(x,y), f x, f y, f xy, f yx опред. в некот. окрест. точки М0(x0,y0). Если f xy, f yx непр. в точке М0(x0,y0), то f xy=f yx в точке М0(x0,y0).
-
z=f(x,y); x,y – независим. перемен.; dz=f x(x,y)dx+f y(x,y)dy
Дифф. от дифф. 1-го порядка от ф-ции z=f(x,y) в любой точке M(x,y), вычисленный на тех же приращениях аргументов ∆х и ∆y, назыв. дифф. 2-го порядка.
d(dz)=d2z=d(f xdx+f ydy)=[dx=∆х=const; dy=∆y=const]=d(dz)=d2z=d(f x(x,y)dx+f y(x,y)dy)=
= (f xdx+f xydy)dx+(f yxdx+f y2dy)dy=[f xy=f yx]=f x2dx2+2f xydx dy+f y2dy2
d2z=(d2f/dx2)dx2+2(d2f/dx dy)dx dy+(d2f/dy2)dy2
d=(d/dx)dx+(d/dy)dy; df=(df/dx)dx+(df/dy)dy; d2f=((d/dx)dx+(d/dy)dy)2f=
= ((d2/dx2)dx2+(d2f/dx dy)dx dy+(d2/dy2)dy2)f
d3f=d(d2f)=((d/dx)dx+(d/dy)dy)3f
dnf=((d/dx)dx+(d/dy)dy)nf
Билет 26
Формула Тейлора для ф-ции неск.переменых.
u=f(M), k+1-раз. дифф в опр. т. М0€[М]
![]() └→(Rk+1(N))
└→(Rk+1(N))
N отр М0М, u=f(M), k-1 раз.дифф. в окр. k раз дифф в т. М0.
![]() ;
;
![]()
Билет 27
Локальный экстремум ф-ции нескольких переменных.
u=f(M)=f(x1,x2,..,xn) опред. в окр. т.М0 (x10,x20,..,xn0).
Опр. Ф-ция u=f(M) имеет в т. М0 локальный максимум (мин.), если сущ. такая окр. в т. М0 в кот.при ММ0 выполняется след. нер-во: f(M)<f(M0), (f(M)>f(M0)).
∆u=f(M)-f(M0)<0, если М0 т.локал. мах.; ∆u>0, если М0 т.локал. мin.
Теор.(необход.усл.экстремума).
Если ф-ция u=f(M) дифф. в т.М0 и М0 – т.лок. max (min), то в этой точке:
Д![]() ок-во:
док-ем, что
ок-во:
док-ем, что
![]() ,
u=f(x1,x2,..,xn)
,
u=f(x1,x2,..,xn)
x2=x20, М0 (x10,x20,..,xn0).
x3=x30,..
xn=xn0.
u=f(x10,x20,..,xn0)
– имеет лок. экстремум в т.М0 →![]() .
.
Точка в кот. все частные призвод. u=f(M) – стационарн., таким обр. точками возможен. экстремума дифф. экстремума явл. стационар. т., но в стационар. т. ф-ция может и не иметь экстремума.
u=xy2, ux’=y2=0; uy’=2xy=0; M(0,0) стационар., но не явл. т.экстремума.
∆u=u(M)-u(M0)= xy2>(<)0
Кроме того, лок. экстр. ф-ция может иметь в т., в кот. она не дифф.:
z=1-√x2+y2; zx’=x/√x2+y2; zy’=y/√x2+y2; z(0,0)=1; z(∆x,∆y)<1
Теор.(Дост. усл. сущ. т. лок. экстр.)
Пусть u=f(u) дважды непр. дифф. в некот. окр.т.M0 и т.M0 – стационар.т., u=f(M) (df(M0)=0), тогда если для любых dx1,dx2,..dxn не равных одновременно 0:
d2f(M0)>0, то т.M0-т.лок.min; d2f(M0)<0, то т.M0-т.лок.max;
Д-во: f(M)=f(M0)+df(M0)/1!+d2f(N)/2!.
∆f(M0)=f(M)-f(M0)=df(M0)+d2f(N)/2!.
u=f(M) – дважды непр. дифф.
d2f(M0)>0→d2f(N)>0; d2f(M0)<0→d2f(N)<0;→ ∆f(M0)>0→
M0 – т.лок. min; M0 – т.лок. max;
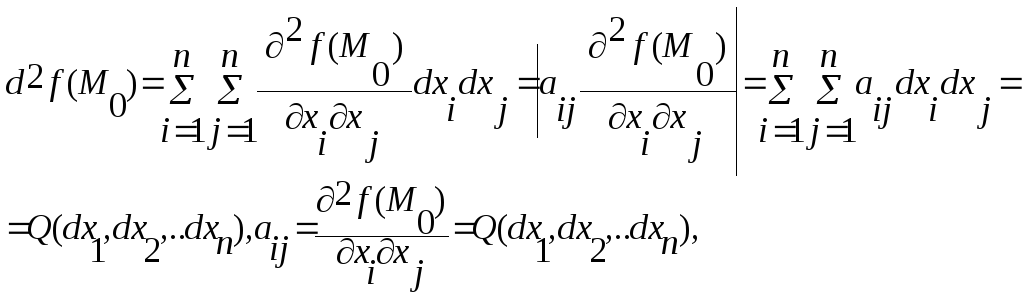
![]()
-
d
 2f(M0)>0↔a11>0,
2f(M0)>0↔a11>0,
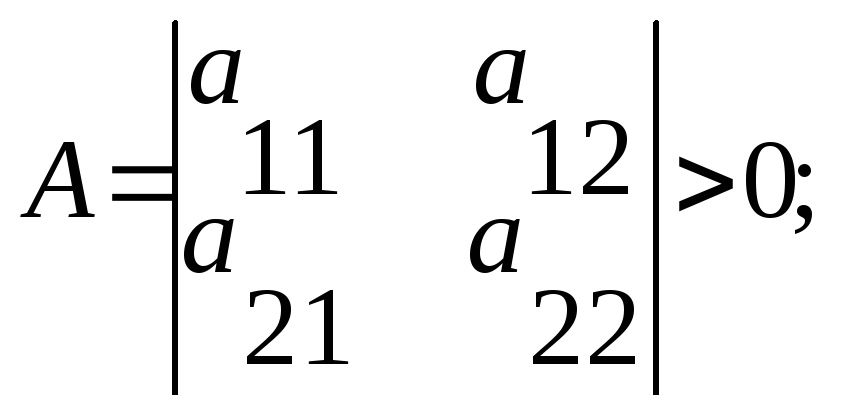
-
d2f(M0)<0↔a11<0,
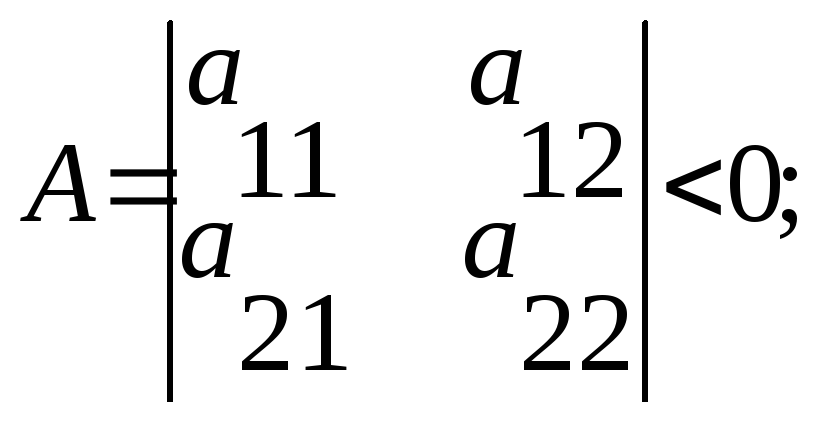
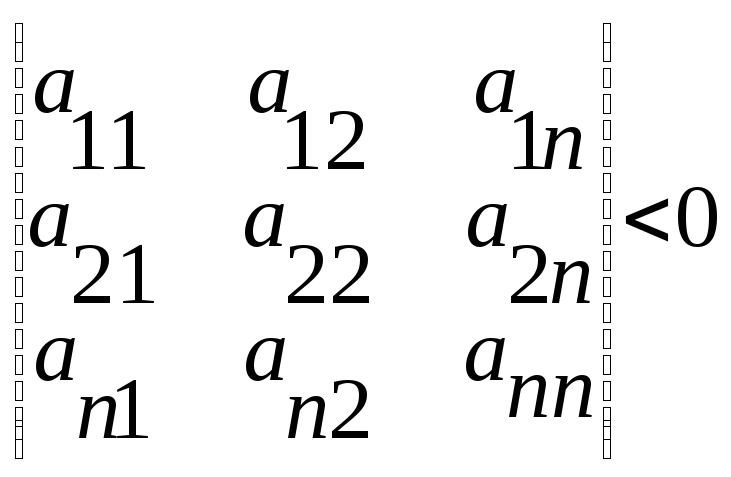
Если d2f(M0) представляет собой закономерную квадрат. форму, то в т. M0 экстремума не будет. Если 2-ой дифф. представляет собой квадр. форму
Q(dx1,dx2,..dxn)>0 то полож.опр.
Q(dx1,dx2,..dxn)≥0 то казизнакополож.опр
х12+2х12х22+х22+(х1+х1)2≥0; х1=-х2.
