
Билет 41.
Формула Стокса.
Пусть гладкая xyz-проетируемая
ориентированная поверхность
![]() ограничена кусочно гладким контуром
ограничена кусочно гладким контуром
![]() и пусть в некоторой 3х мерной области,
содержащей в себе поверхность
и пусть в некоторой 3х мерной области,
содержащей в себе поверхность
![]() ,
ф-ции P,Q,R
и их частные проихводные непрерывны,
тогда справедливо следующее:
,
ф-ции P,Q,R
и их частные проихводные непрерывны,
тогда справедливо следующее:
 ,
,
где направление обхода контура
![]() осуществляется в положительном
направлении.
осуществляется в положительном
направлении.
Если граница
![]() состоит из нескольких контуров, то
формула Стокса остается в силе. При этом
в левой части надо написать сумму
интегралов по всем контурам, пробегаемым
в положительном направлении.
состоит из нескольких контуров, то
формула Стокса остается в силе. При этом
в левой части надо написать сумму
интегралов по всем контурам, пробегаемым
в положительном направлении.
Для вычисления интегралов по замкнутому
контуру
![]() можно
выбрать любую поверхность
можно
выбрать любую поверхность
![]() ,
ограниченную контуром
,
ограниченную контуром
![]() .
Разумно выбирать поверхность простого
вида.
.
Разумно выбирать поверхность простого
вида.
Условие независимости КРИ-2 от пути интегрирования.
3х мерная область V
называется поверхностно односвязной,
если для любого замкнутого контура
![]() ,
лежащего в V внутри V
найдется поверхность, ограниченная
,
лежащего в V внутри V
найдется поверхность, ограниченная
![]() .
.
![]() и
их частные производные 1го порядка
непрерывны в некоторой замкнутой
ограниченной поверхностью односвязной
области V, то след. 4 условия
эквивалентны:
и
их частные производные 1го порядка
непрерывны в некоторой замкнутой
ограниченной поверхностью односвязной
области V, то след. 4 условия
эквивалентны:
1)
![]() любого
замкнутого кусочногладкого контура
любого
замкнутого кусочногладкого контура
![]() -
-
![]()
2)
![]() не
зависит от пути соединения точек А и В.
не
зависит от пути соединения точек А и В.
3)
![]() полный
диф-л, где
полный
диф-л, где
![]()
4)
![]()
Билет 28.
Условный экстремум ф-ции нескольких переменных.
Найти экстремум z, при ксловии, что x и y связаны следующим образом.
![]() ;
x+y-1=0;
;
x+y-1=0;
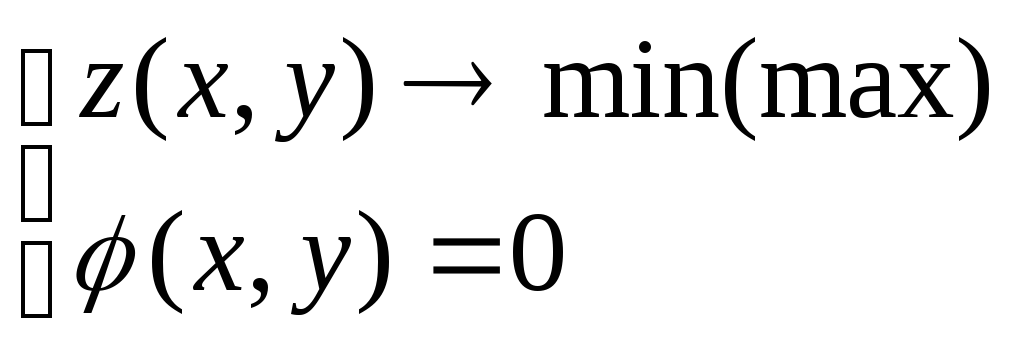 (*)
(*)
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Метод множителя Ла-Гранджа.
(*) эквивалентна задаче:
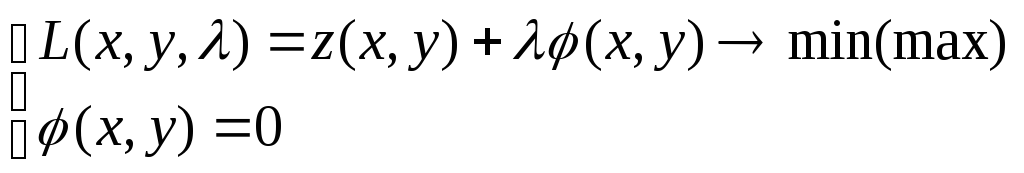 ,
где
,
где
![]() -множитель Ла-Гранджа;
-множитель Ла-Гранджа;
![]() - функция Ла-Гранджа.
- функция Ла-Гранджа.
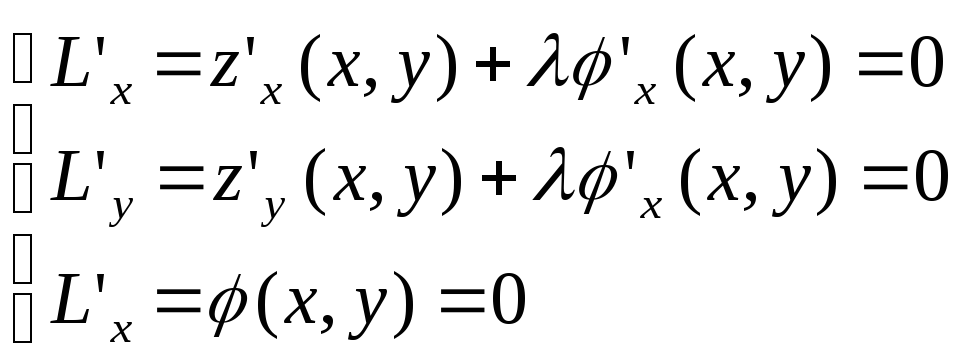
Надо исследовать
![]() ф-ции Ла-Гранджа с учетом условия связи
в диффиринциалах.
ф-ции Ла-Гранджа с учетом условия связи
в диффиринциалах.
Наибольшее и наименьшее значение ф-ции в замкнутой области.
Если ф-я определена в замкнутой ограниченной области Д, то она достигает своего min и max значения, либо в стационарных точках внутри области, либо на ее границе.
Билет 29.
Интегралы по фигуре от скалярной ф-ции.
Множество называется связанным, если любые 2 из них можно соединить линией, все точки которой принадлежат данному множеству.
Под геометрической фигурой![]() понимается одно из следующих связных
(включая границу) множеств точек (см.
таблицу).
понимается одно из следующих связных
(включая границу) множеств точек (см.
таблицу).
Диаметром d фигуры Ф называется максимальное расстояние между двумя ее точками.
Под мерой![]() фигуры Ф понимается следующее (см.
таблицу).
фигуры Ф понимается следующее (см.
таблицу).
![]() Если он существует, конечен и не зависит
от способа построения интегральной
суммы
Если он существует, конечен и не зависит
от способа построения интегральной
суммы
![]() ,
то он называется интегралом по фигуре
Ф от скалярной ф-ции Ф(Р) и обозначается
,
то он называется интегралом по фигуре
Ф от скалярной ф-ции Ф(Р) и обозначается
![]()
Теорема: Если на связной, ограниченной и содержащей граничные точки фигуре Ф скалярная ф-ция f(P) непрерывна, то интеграл по фигуре Ф существует.
Билет 30.
Свойства интегралов по фигуре от скалярной ф-ции.
1).
![]()
2).
![]()
3).
![]()
4).
![]()
![]() ;
;
![]() -
длина линии L;
-
длина линии L;
![]() ;
;
![]() ;
;
![]()
5). Если
![]() то
то
![]()
6). Если
![]() ,
то
,
то
![]()
7). Если
![]() ,
то
,
то
![]()
8). Теорема о среднем: Если f(p)
непрерывна на фигуре Ф, причем Ф –
ограничена о содержит граничные точки,
то
![]()
Геометрические и физические прилажения интегралов по фигуое от скалярной ф-ции.
![]() -
материальная фигура
-
материальная фигура
![]() -
плотность материальной йигуры Ф
-
плотность материальной йигуры Ф
![]()
![]()
![]()
![]()
![]()
![]()
Билет 31.
Криволинейный интеграл 1го рода.
![]() 1).
1).
![]() ;
;
![]() - диф-ма на [a,b];
- диф-ма на [a,b];
![]()
![]() ;
L: x=g(y);
;
L: x=g(y);
![]()
![]() ;
;
2).
![]() ;
x(t),y(t)
– непрерывно диф-ма на
;
x(t),y(t)
– непрерывно диф-ма на
![]() ;
L:
;
L:
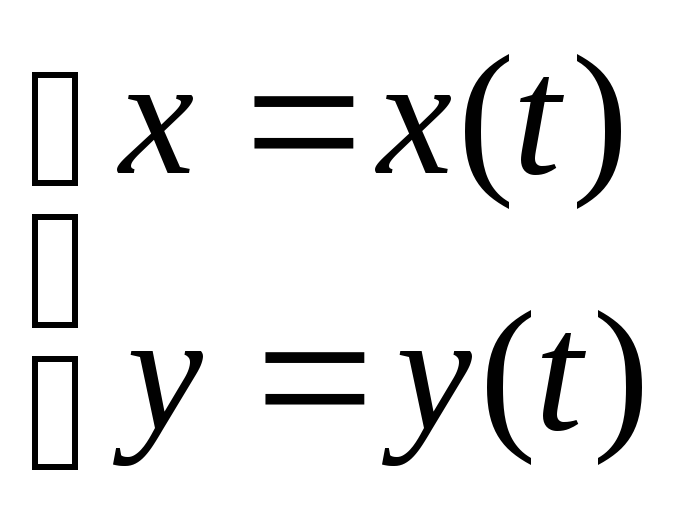
![]()
![]() ;
;
3).
![]() ;
;![]() ;
L:
;
L:

![]()
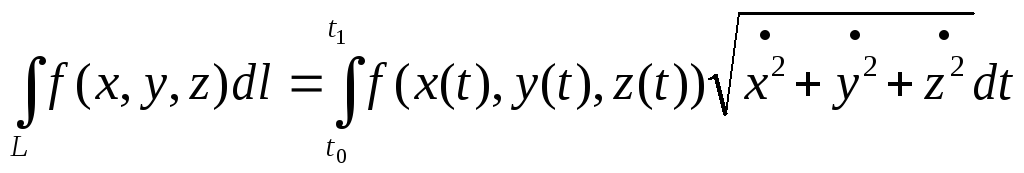
4).
![]() ;
;
![]() ;L:
;L:
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]()
Билет 36.
Интеграл по ориентированной фигуре от векторной ф-ции.
![]()
Векторная ф-ция 3х переменных
x,y,z,
определенной на фигуре Ф. Ф-ции P,Q,R
называются координатами
![]() .
Фигура Ф называется ориентированной,
если в каждой ее точке М задан некоторый
вектор
.
Фигура Ф называется ориентированной,
если в каждой ее точке М задан некоторый
вектор
![]() ,
характеризующий эту фигуру. Диния
,
характеризующий эту фигуру. Диния
![]() называется ориентированной, если на
ней выбрано направление перемещения.
называется ориентированной, если на
ней выбрано направление перемещения.
Гладкая поверхность называется двусторонняя, если нормаль к ней при обходе по замкнутому контуру, лежащему на поверхности и не имеющему общих точек с ее границей, возвращается к своему первоначальному положению.
1).
![]() ;
2).
;
2).
![]() ;
3).
;
3).
![]() ; 4).
; 4).
![]()
5).
![]() ; n-я интегральная сумма
для векторной ф-ции a(M)
по ориентированной с помощью вектора
P(n)
фигуре Ф. ; 6).
; n-я интегральная сумма
для векторной ф-ции a(M)
по ориентированной с помощью вектора
P(n)
фигуре Ф. ; 6).
![]() (*)
(*)
Если (*) существует, конечен и не зависит
от способа построения интегральной
суммы
![]() ,
то он называется интегралом по
орентированной фигуре Ф от векторной
ф-ции a(M).
,
то он называется интегралом по
орентированной фигуре Ф от векторной
ф-ции a(M).
![]()
![]()
P(x,y,z) Q(x,y,z) R(x,y,z) a=(P,Q,R)
Если ф-ции P,Q,R непрерывны на гладкой, ограниченной, содержащей граничные точки ориентированной фигуре Ф, то интеграл существует.
Частные случаи интегралов по ориентированной фигуре.
Свойства интеграла по фигуре от векторной ф-ции.
1).
![]() ;
2).
;
2).
![]() ,
c=const
,
c=const
3).
![]() ; 4).
; 4).
![]()
Билет 4.
Понятие первообразной ф-ции и неопределенного интеграла.
Пусть ф-ция f(x) определена на X. Ф-ция F(x) – первообразная для f(x) на X, если F’(x)=f(x) для любого x € X.
F(x) – первообразная, F(x)+C – первообразная.
![]()
![]() для
для
![]()
![]() ;
;
![]()
Совокупность всех первообразных F(x)+C
для ф-ции f(x),
определенное на X, называется
неопределенным интегралом от ф-ции f(x)
на X и обозначается
![]()
![]() ;
;
![]()
Основные свойства неопределенного интеграла.
1).
![]()
2).
![]()
![]()
3).
![]()
4).
![]()
![]()
Билет 5.
Замена переменной в неопределенном интеграле.
Внесение множителя под знак диффиринциала.
Теорема: Пусть![]() определена
и диф-ма на X. U-
множество значений ф-ции
определена
и диф-ма на X. U-
множество значений ф-ции
![]() .
Для f(U)
существует F(U)
на U.
.
Для f(U)
существует F(U)
на U.
![]() Тогда для g(x)
на X сущ-т первообразная
Тогда для g(x)
на X сущ-т первообразная
![]() ,
т.е.
,
т.е.
![]()
Док-во:
![]()
На практике:
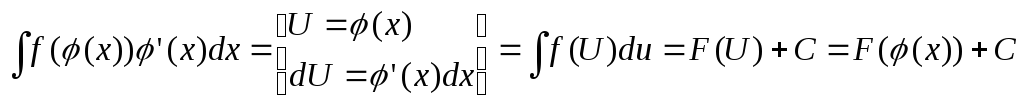
Вынесение множителя из-под знака дифференциала.
Теорема: Пусть![]() определена и диф-ма на T.
определена и диф-ма на T.
![]() на
Т. Для g(t)
на Т существует G(t).
на
Т. Для g(t)
на Т существует G(t).
![]() ,
тогда для f(x)
на X существует первообразная
,
тогда для f(x)
на X существует первообразная
![]() .
.
![]()
Док-во:
![]() возрастающая
возрастающая![]() гарантировано
гарантировано
![]() (обратная).
(обратная).
![]()
На практике:

Билет 42.
Скалярные поля. Производная по направлению. Градиент.
Пусть V – некоторая область
в пространстве. Говорят, что в этой
области задано скалярное поле, если
каждой т.
![]() поставлено
в соответствие некоторое число U(M)
(пример – поле температур, освещенности).
Скалярное поле не зависит от выбора
системы координат. Поверхность или
линия, на которой U(M)
принимает постоянное значение называется
поверхностью уровня скалярного поля.
поставлено
в соответствие некоторое число U(M)
(пример – поле температур, освещенности).
Скалярное поле не зависит от выбора
системы координат. Поверхность или
линия, на которой U(M)
принимает постоянное значение называется
поверхностью уровня скалярного поля.
Пусть U(M) –
некоторое скалярное поле.
![]() -
единственный фиксированный вектор.
-
единственный фиксированный вектор.
![]() -фиксированая
точка.
-фиксированая
точка.
![]() ;
;
![]() ;
;
![]()
Если
![]() ,
то он называется производной скалярного
поля U(M) по
направлению
,
то он называется производной скалярного
поля U(M) по
направлению
![]() в точке
в точке
![]() .
.
![]()
lnH-скорость изменения
ф-ции U(m) по
направлению
![]() в точке
в точке
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]()
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() принимает наибольшее значение при
принимает наибольшее значение при
![]() ,
т.е. в направлении вектора gradU
в т.
,
т.е. в направлении вектора gradU
в т.
![]()
gradU указывает направление наибольшего роста поля в данной точке. | gradU| - скорость роста ф-ции U в данном направлении. Вектро gradU не зависит от выбора системы координат. Grad направлен по поверхности уровня в данной точке.
