Билет 1.

Комплексные числа.

Комлексным числом Z наз. число z=x+iy, где x, y R.

Мн-во комплексных чисел – С, R C, x–действ. часть, y – мнимая часть.

Расстояние от z(x,y) до начала корд. наз. модулем комп. числа Z. Аргументом числа Z 0, наз угол , кот-й образует радиус-вектор точки Z и полож направл оси OX.

Argz = argz (главное знач аргумента) + 2k kZ

-<argz<

argz =

z = x+iy=zcos+izin=z(cos+isin)

z=r(cos + isin) (!)

z1 = r1(cos + isin)

z2 = r2(cos + isin) тогда

z1*z2 = r1*r2(cos(1+ 2) + isin(1+ 2)

zⁿ = rⁿ(cos(n) + isin(n)

- Формула Муавра (!)

Формулы Эйлера:

; (!)

; ; ;

Билет 20.

Предел функции нескольких переменных.

Опр. т. А наз. пределом посл-ти (Mn) если для любого Е(эпсилон) сущ. N-N(E); любое n>=N(E) => p(Mn,A) < E; ; (число)

(x₁, x₂, …,x_m)-независимые переменные.

Опр по Коши: число b наз пределом ф-ии u=f(M) в т. А (при ), если для любого Е > 0 сущ. , для любого

Опр по Гейне: число b наз пределом посл-ти ф-ии u=f(M) в т. А, если для любого (Mn),

A(a₁, a₂,…, a_m)

Теор. Если сущ. и сущ. , то сущ. , причем

Опр. u=f(M) наз. непрерывной в т. А, если

M(x₁, x₂, …,x_n) ; … ; A(a₁, a₂, …,a_n)

Опр2. u=f(M) наз. непрерывной в т. А, если

Точка в к-й ф-я не определена или не является непрерывной, наз. точками разрыва этой ф-ии.

(24) Геометр. Смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.

f (x,y)=f(x₀,y₀)+A∆x+B∆x+o(ρ); z₀=f(x₀,y₀); z=f(x,y); ∆x=x-x₀, ∆y=y-y₀;

z₀=z₀+A(x-x₀)+B(y-y₀); z₀-z=A(x-x₀)+B(y-y₀);

z₀-z=f_x‘(x₀,y₀)(x-x₀)+f_y‘(x₀,y₀)(y-y₀)-ур-ние касательн. плоскости в поверхности.

z=f(x,y) (x₀,y₀,z₀).

Нормалью к поверхн. в данной точке М₀(x₀,y₀,z₀) назыв. прямая, проходящая через эту точку перпенд. к касат.

(x-x₀)/f_x‘(x₀,y₀)=(y-y₀)/f_y‘(x₀,y₀)=(z-z₀)/(-1) – ур-ние нормали

(x-x₀)/f_x‘(x₀,y₀,z₀)=(y-y₀)/f_y‘(x₀,y₀,z₀)=(z-z₀)/f_z‘(x₀,y₀,z₀)

Билет 2.

Многочлены.

Многочлен (полином) относительно переменной z - это

2z⁴-5z³+2z=(z²-1)(2 z²-5z+2)+(-3z-2)

Q_m(z) T_k(z) R_c(z)

Значит P_n(z) = Q_m(z) T_k(z) + R_c(z) (*), где m<=n m+k=n, l<n;

Если R_c(z) = 0, то P_n(z) делится на Q_m(z).

Назовем компл. число z₁ корнем многочл. P_n(z), если P_n(z₁).

Теор. БЕЗУ: многочлен не нулевой степени P_n(z) делится на двучлен z-z₁, тогда и только тогда, когда z₁ является корнем P_n(z).

Запишем (*) для P_n(z) и z-z₁: P_n(z) = (z-z₁)T_n-1(z)+ R_c(z) => z:=z₁.

Основная теорема алгебры(Гаусса): всякий многочлен P_n(z) не нулевой степени имеет по крайней мере 1 комплексный корень.

Компл. число z₁ наз. корнем кратности к₁ многочл. P_n(z), если

P_n(z) = (z-z₁)^к1Т_n-k1(z)

Следствие: Многочл. P_n(z) имеет n комлексных корней с учетом их кратности:

P_n(z) = a_n(z-z₁)^к1(z-z₂)^к2…

Пусть z₁ – корень P_n(z) с действ. коэф-ми, тогда корень P_n(z)

P_n()===0

Комплексно-сопряж. корни входят в разложение многочлена парами.

(z-z₁)(z-)=z²+p₁z+q₁

P_n(x) – с действ. коэф.

P_n(x)=a_n(x-x₁)^k1(x-x₂)^k2*…*(x-x_l)^kl(x²+p₁x+q₁)^R1(x²+p₂x+q₂)^R2*…*(x²+p_mx+q_m)^Rm

x₁, x₂,…,x_n – действ. корни

k₁, k₂,…,k_n – их кратности

P₁, P₂,…,P_n, q₁, q₂,…,q_n – действ. числа

k₁+k₂+…+k_l+2R₁+2R₂+…+2R_m = n

Билет 33.

Замена переменной в двойном интеграле.

( *)

Свойства

1. x(u,v), y(u,v) – взаимно однозначны

2. x(u,v), y(u,v) – непрерывные, непр. частн. пр-е 1-го порядка

3. 

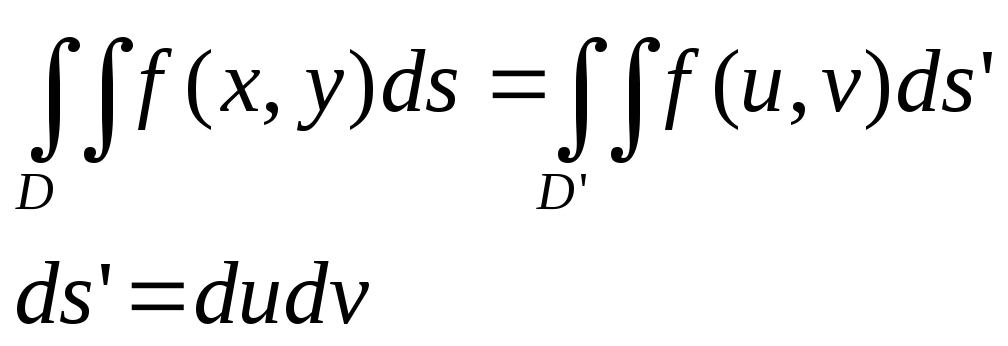
P₁: x(u,v), y(u,v)

P_2: x(u+_∆u,v), y(u+_∆u,v)

I – Якобиан(Якоби)

Модуль I – коэффициет растяжения площади в т. с координатами u и v при отображении D на D’.

Вычисление в полярной сист координат.

,

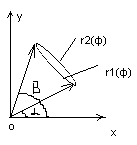
a)

b )

c)

Билет 38.

Формула Грина.

Область наз. односвязной если в ней любой замкнутый контур может быть стянут в точку с помощью непрерывной деформации, при к-й не границы области не пересекаютя.

Область D наз. односвяз., если каков бы ни был замкн. контур l , лежащий внутри этой области, ограниченная этим контуром конечн. часть пл-ти целиком принадл. D.

Порстая область: замкн. пл-ть D (обл. вместе с её границами) – её можно разбить на конечное число как y- так и x- трапецивидных областей.

Например: круг, прямоугольник, кольцо.

Теор. Грина: пусть P(x,y), Q(x,y) и и непрерывны в простой области D тогда

где L – граница области D, к-я обходится в положительном направлении.

Док-во

Предположим D – односвяз. область, огр. L – полож. ориентир. Предположим, что оюл. D такова, что прямые параллельн. осям пересекают ее не более, чем в 2-х точках.

Для I₂ – аналогично.

Формула Грина имеет место для любой простой области.

Если контур обходится в обратном направлении, то перед двойным интегралом ставится «-».

3) Рациональные дроби.

Опр. , где Pn(z), Qm(z) – многочлены, наз. рациональной дробью.

n>=m – дробь неправильная; n<m – правильная.

Разложение правильной рац. дроби с комплексными коэф. на сумму простейших дробей.

Если - правильная дробь, то , где

z₁, z₂,…, z_l – разл. компл. корни

k₁, k₂,…, k_l – их кратности

то сущ. Такие компл. числа A_i^k, где i=1,2,…,l; k=1,2,…,k_i, то тогда

Разложение простой рац. дроби с действ. коэф. на сумму простейших дробей с действ. коэф.

Пусть - правильная дробь,

x₁, x₂,…, x_l – разл. компл. корни

k₁, k₂,…, k_l – их кратности

p_i²-4q_i<0 для i=1…s

R₁, R₂,…,R_s – кратности пар корней, тогда

+Метод неопределенных коэффициентов + Метод частных значений

Билет 8.

Интегрирование тригонометрических функций.

tg(x/2)=t – универсальная тригоном. подстановка.

; ; ;

Специальная тригоном. подстановка:

1. R(-sinx,cosx)dx = -R(sinx,cosx), тогда cosx = t;

2. R(sinx,-cosx)dx = -R(sinx,cosx), тогда sinx = t;

3. R(-sinx,-cosx)dx = -R(sinx,cosx), тогда tgx = t;

Интегралы вида:

1. m,n Z, m,n >= 0;

1. Одно из чисел m, n – нечетное, тогда sinx=t,cosx=t;

2. Оба нечетные или четные -

2. m,n Q

это дифференц. Бином

- для гиперболических функций аналогично

Универсальная подстановка – th(x/2) = t, и так далее…

Билет 9.

Интегрирование иррациональных функций.

; ; n1,n2…N, m1,m2…Z

, где s-общий знаменатель дробей m1/n1, m2/n2 …

, тогда

Вид интеграла	Тригоном. подстановка	Иррацион. подстановка

m,n,p Q; a,b R

1) p Z, тогда , где s-общий знаменатель дроби

2)

3) , где s- знаменатель дроби

Во всех остальных случаях интеграл не выражается, т. е. является не берущимся.

Билет 15.

Вычисление площадей плоских фигур.

1. В 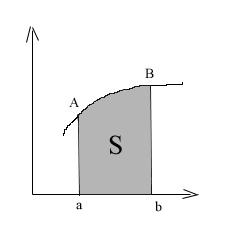декартовой системе координат

f(x)-непрерывна

x=a,x=b; отр [a,b] оси оХ

2. В параметрическом виде.

; ;

разбиваем: ;

3. В полярной системе координат

; ; ; ;

; ;

Билет 18.

Определение НИ-1.

Пусть f(x) определена на и инт на ; , т.е.

Пусть

Если этот lim существует и конечен, то говорят, что НИ-1 сходится. Если не существует или бесконечен, то расходится.

;

Свойтсва НИ-1.

1. Аддитивность

Если сходится, то , ;

2. Линейность

Если сходится и сходится, то сходится и

Вычисление и преобразование НИ-1.

Формула Нбютона-Лейбница.

Если f(x) непрерывна на и F – какая-то первообразная для ф-ции f(x), то

Интегрирование по частям.

Если U,V – непрер. Диф-мы ф-ции на , то

Исследование на сходимость.

Т1: Пусть ф-ции f(x) и g(x) , тогда если и , то

сходится сходится

расходится пасходится

Предельный признак сравнения для НИ-1.

Т2: Пусть, ; , тогда если конечный , то и сходятся или расходятся одновременно.

При k=1 при

Т3: Если и сходится, то сходится.

Определение: называется абсолютно сходящимся, если сходится .

Если расходится, а сходится, от - неабсолютно (условно) сходящийся .

Главное значении.

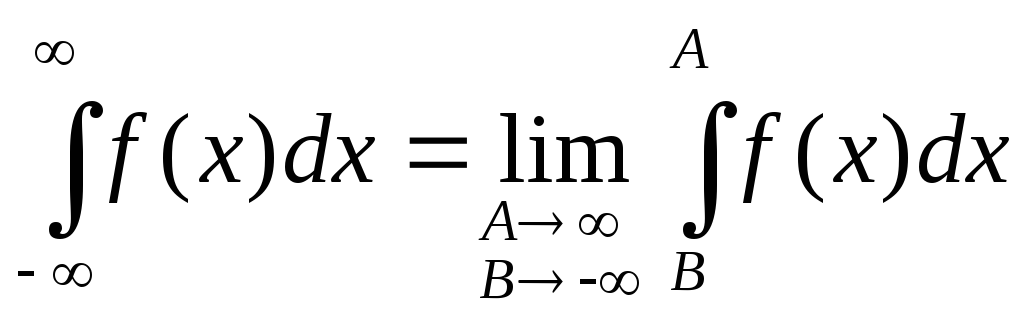
Главным значением называется ; VP-Value principul

Если и сходится, то и