2. Поняття про зони Бріллюена

Згідно з гіпотезою де-Бройля електрон має хвильові властивості з довжиною хвилі , де h – стала Планка, р = mυ – імпульс. Кінетична енергія . Імпульс можна виразити через хвильове число . Тоді кінетична енергія буде . (4.1)

Ця залежність енергії від хвильового числа називається дисперсійною кривою. Для вільного електрона вона уявляє квадратну параболу.

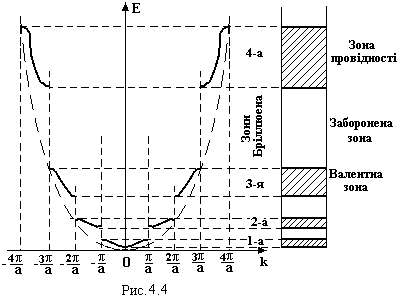
Якщо вільний електрон рухається в кристалі, на нього діє періодичне поле атомів. Розв’язуючи рівняння Шредінгера для електрона, який рухається в періодичному полі, вимога нерозривності хвильової функції та її перших похідних приводить до того, що дисперсійна крива Е(k) (рис.4.4) зазнає розривів при значеннях хвильових чисел k = ±nπ/a, де n = 1, 2,3…, а – період поля (стала кристалічної гратки).

Пунктиром показана дисперсійна крива вільного електрона, суцільною – електрона в кристалі. Інтервали значень хвильового числа k, в межах яких енергія змінюється неперервно, а на границях зазнає розриву, називаються зонами Бріллюена. 1-а зона простирається від –π/а до +π/а, 2-а від -2π/а до -π/а і від + π/а до +2 π/а і т.д. На рис.4.4 показані дисперсійні криві і зони Бріллюена для лінійного одноатомного ланцюга. У трьохмірному випадку зони Бріллюена уявляють собою досить складні замкнуті поверхні - багатогранники, вставлені один в один. Їх називають дисперсійними поверхнями

Відмітимо загальні властивості границь зон Бріллюена і зон дозволених значень енергії:

а) Дно зони дозволених значень енергії відповідає мінімуму дисперсійних поверхонь (зон Бріллюена);

б) Стеля зони дозволених значень енергії відповідає максимуму дисперсійних поверхонь (зон Бріллюена).

в) В межах зони Бріллюена між мінімумом і максимумом завжди є точка перегину.

3. Ефективна маса електронів. Поняття про дірки

Для описання поводження електрона в кристалі необхідно знати форму дисперсійних поверхонь. Але досконала їх форма не завжди відома та виявляється не завжди і потрібна. Достатньо сформульованих вище трьох загальних властивостей. Вияснимо, як впливають ці властивості на поводження електрона в кристалі?

Для вільного електрона дисперсійна крива описується рівнянням (4.1). Візьмемо з цього рівняння похідну по хвильовому числу k і знайдемо його

. (4.2)

Тоді імпульс електрона , а його швидкість

. (4.3)

Нехай на електрон з боку електричного чи магнітного поля діє деяка сила. Знайдемо прискорення, взявши з виразу (4.3) похідну за часом

. (4.4)

З другого боку по другому закону Ньютона імпульс сили дорівнює зміні імпульсу Fdt = dp, або, враховуючи, що р = ћk, одержуємо

. (4.5)

Підставимо (4.5) в (4.4) ,

де ефективна маса 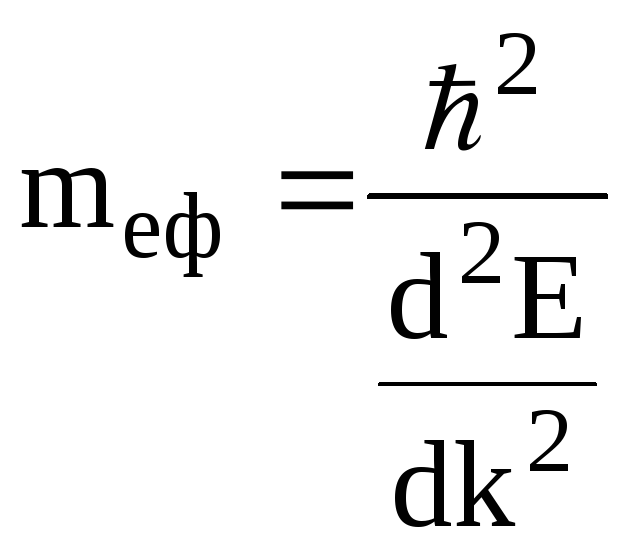. (4.6)

Ефективна маса враховує властивість другої похідної із дисперсійної кривої, тобто вплив силового поля кристалу на рух у ньому електронів. Проаналізуємо залежність (4.6) в особливих точках дисперсійних кривих. Видно, що знак і величина m_еф визначається другою похідною.

а) Поблизу дна зони дозволених значень енергій дисперсійна крива зазнає мінімуму. Як відомо, у цьому випадку друга похідна із функції позитивна. Отже і m_еф > 0.

б) Біля стелі зони дисперсійна крива зазнає максимуму і друга похідна із функції негативна. Отже і m_еф < 0 ! Це означає, що прискорення електрона в кристалі протилежне тому, яке мав би вільний електрон. Наприклад, в електричному полі вільний електрон рухається проти напруженості, а в кристалі у випадку m_еф < 0 по полю. Причиною цього є досить велике внутрішнє поле кристалу, яке переважає прикладене зовнішнє поле. Тому для спостерігача здається, що електрон веде себе як позитивна частинка з позитивною ефективною масою. Таку частинку назвали діркою. У зв’язку з цим були введені поняття ефективної маси електронів m_n і дірок m_p.

в) В точці перегину, тобто поблизу середини зони дозволених значень енергії, друга похідна дорівнює нулю, а ефективна маса прямує до нескінченності. Це випадок, коли сила зв’язку електрона настільки велика, що зовнішнє поле не може привести електрон у прискорений рух.

г) Ефективна маса як електронів, так і дірок може бути більшою, або меншою від маси спокою вільного електрона m. Наприклад, для германію m_n=0,56m, m_p=0,59m; для кремнію m_n=1,08m, m_p=0,37m. Це знову таки зумовлено впливом внутрішнього поля кристалу. У випадку воно допомагає дії зовнішньої сили ефективна маса менша маси спокою вільного електрона, а коли протидіє – більша.