Вопрос №1

Основные свойства преобразования Фурье:

1. Сложение, усиление и ослабление сигналов (теорема линейности)

2. Сдвиг сигнала во времени (теорема запаздывания)

3. Смещение спектра сигнала (теорема смещения)

4. Изменение масштаба времени.

5. Спектр произведения сигналов (теорема о свертке спектров)

6. Умножение сигнала на гармоническую функцию.

Сигнал в виде d-функции, его свойства.

Дельта-функция - теоретическая модель беско­нечно короткого импульса с бесконечно большой амплитудой (рис а).

Функцию d(t)называют дельта-функцией, единичным импульсом, функцией Дирака.

Рис. 2.20. Дельта-функция:

а — графическое представление;

б — дельта-функция в виде прямоугольного импульса; в — спектральная плотность

Сигнал в виде дельта-функции невозможно реализовать фи­зически. Однако теоретически дельта-функцию можно рассматривать как пре­дел, к которому стремится прямоугольный импульс длительностью т_и и ампли­тудой 1/т_и при т_и —> 0 (рис. 2.20, б).

Дельта-функция обладает важнейшим свойством, благодаря которому она получила широкое применение в математике, радиотехнике, теории связи и т. д. Пусть имеется непрерывная функция (аналоговый сигнал) времени f(t). Тогда справедливо следующее соотношение:

Это соот­ношение характеризует фильтрующее (выделяющее, или стробирующее, от слова «строб» — короткий прямоугольный импульс, применяемый в радио­локации для выделения сегментов колебаний) свойство дельта-функции.

Соотношение между длительностью сигнала и шириной его спектра.

Чем меньше длитель­ность сигнала, тем шире его спектр.

Это фундаментальное положение теории сигналов можно установить в общем виде на основе преобразования Фурье

Чем короче сигнал, тем выше граничная частота спектра сигнала. Так как нижняя граница спектра примыкает к нулевой частоте (имеются в ви­ду сигналы без высокочастотного заполнения, как, например, на рис. 2.23, а), то спектр получается тем шире, чем короче сигнал.

Рис. 2.23. К вопросу о со­отношении между дли­тельностью сигнала и ши­риной его спектра

Вопрос 2

2.1 Спектры некоторых неинтегрируемых функций: гармонический сигнал, единичная функция включения (функция Хевисайда).

Спектр сигнала может быть найден при условии абсолютной интегрируемости:

Некоторые функции, такие как, гармонический сигнал и единичная функция включения (функция Хевисайда) не отвечают этому условию. Устранить данное препятствие позволяют свойства дельта-функции.

Рассмотрим гармонический сигнал: s(t) = A₀*cos(w₀t + θ₀).

Не обращая внимание на то, что такой сигнала не является абсолютно интегрируемым, запишем:

И спользую формулу,

запишем:

Применяя эту формулу ко всем гармоникам любого периодического сигнала

получим спектральную плотность гармонического сигнала:

Найдем спектральную плотность единичного скачка.

Эту функцию запишем виде:

½ + ½*sign(t),

где sign(t) – сигнум функция, равная единице, при переходе переменной t через 0 знак ее изменяется.

Спектральная плотность постоянной составляющей - πσ(w).

Продифференцировав функцию ½*sign(t) получим производную, равную нулю на всей оси времени кроме t = 0, она равна σ(t). Спектральная плотность σ(t) равна единице, следовательно спектральная плотность сигнум-функции 1/iw.

Тогда спектральная плотность единичного скачка равна:

S(w) = πσ(w) + 1/iw.

2.2 Представление сигналов на плоскости комплексной частоты.

Введем понятие комплексной частоты: p = σ+iω.

Представим функцию s(t) в следующем виде:

s(t) = s₊(t) + s_–(t),

где s₊(t) задана при 0<t<∞;

s_–(t) задана при -∞<t<0.

Перейдем от переменной ω к переменной p для функции s₊(t).

1. Домножим s₊(t) на , где выберем так, чтобы обеспечивалась интегрируемость функции в пределах 0<t<∞.

2. Получим следующее:

(2.1)

где - спектральная плотность функции .

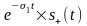3. Подставив iω =p - σ₁ и ω = (p - σ₁)/i в выражение (2.1) получим:

откуда следует:

(2.2)

Функция является спектральной плотностью сигнала и определяется выражением:

откуда

. (2.3)

Полученное выражение (2.3) называют односторонним преобразованием Лапласа функции . А выражение (2.2) обратным преобразованием Лапласа.

Так же поступим для функции s_–(t), заданной при - ∞<t<0. Домножив s _– (t) на , где выбранной так, чтобы обеспечивалась интегрируемость функции в пределах -∞<t<0 запишем:

Запишем следующее:

– двустороннее преобразование Лапласа.

Вопрос 3.

ПРЕДСТАВЛЕНИЕ СИГНАЛОВ С ОГРАНИЧЕННОЙ ЧАСТОТНОЙ ПОЛОСОЙ В ВИДЕ РЯДА КОТЕЛЬНИКОВА

В теории и технике сигналов широко используется теорема Котельникова (теорема отсчетов): если наивысшая частота в спектре функции s (t) меньше чем f_m, то функция s (t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на 1/2 f_m секунд.

В соответствии с этой теоремой сигнал s(t), ограниченный по спектру наивысшей частотой ω_m = 2π f_m, можно представить рядом

В этом выражении 1/2 f_m = Δt обозначает интервал между двумя отсчетными точками на оси времени, a s (n/2f_m) = s(nΔt) — выбор­ки функции s (t) в моменты времени t = nΔt.

Представление заданной функции s (t) рядом (2.120) иллюстри­руется рис. 2.35.

Функция вида

уже встречавшаяся ранее, обладает следую­щими свойствами:

а) в точке t = nΔt φ_n(nΔt) = 1, а в точках t = kΔt, где k — любое целое положительное или отрицательное число, отличное от п, φ_n(kΔt) = 0;

б) спектральная плотность функции φ₀ (t) равномерна в полосе частот |ω| < ω_m и равна 1/2 f_m = π/ω_m [см. (2.82) и рис. 2.20, б].

Рис. 2.35. Представление сигнала рядом Котельникова.

Так как функция φ_n (t) отличается от φ₀ (t) только сдвигом на оси времени на величину nΔt, то спектральная плотность функции φ_n (t)

Модуль этой функции изображен в нижней части рис. 2.36 (сплош­ной линией).

То, что ряд (2.120) точно определяет заданный сигнал s (t) в точ­ках отсчета, не требует дополнительных доказательств, поскольку коэффициентами ряда являются сами выборки из функции, т. е. величины s(nΔt). Можно доказать, что ряд (2.120) определяет функ­цию s (t) в любой момент t, а не только в точках отсчета t = nΔt. Воспользуемся для этого общими правилами разложения функции по ортогональной системе, изложенными в § 2.2. В данном случае разложение производится по функциям вида (2.121), для которых интервал ортогональности равен бесконечности, а норма || φ_n || в соответствии с (2.5)

Не предрешая заранее значения коэффициентов ряда (2.120), применим для их определения общую формулу (2.9), справедливую для обобщенного ряда Фурье:

При этом мы исходим из условия, что s (t) — квадратично интег­рируемая функция (энергия сигнала конечна).

Рис. 2.36. Связь между спектром сигнала s(t) и спектром базисной функции φ_n (t)

Для вычисления интеграла в выражении (2.124) воспользуемся формулой (2.63), согласно которой

Пределы интегрирования здесь приведены в соответствии с за­данной граничной частотой ω_m = 2π f_m в спектре сигнала, а также в спектре функции φ_n (t).

И нтеграл в правой части (2.125) с коэффициентом 1/2л есть не что иное, как значение s (t) в момент t = nAt. Таким образом,

Подставляя этот результат в (2.124), получаем окончательное выражение

с_п = s (nΔt),

из которого следует, что коэффициентами ряда (2.120) являются выборки функции s (t) в точках t = nΔt.

Поскольку ограничение спектра конечной наивысшей частотой обеспечивает непрерывность функции s(t), ряд (2.120) сходится к функции s (t) при любом значении t.

Если взять интервал между выборкам Δt' меньшим, чем Δt = = l/2f_m, то ширина 2f'_т спектра Ф'_п (ω) функции φ'_n будет больше, чем у спектра S (ω) сигнала s (t) (рис. 2.36), но это не отразится на величине коэффициента с_п. Модуль функции Ф' (ω) изображен на рис. 2.36 штриховой линий.

При увеличении же Δt" по сравнению с Δt спектр Ф"_п (ω) функции φ_n (t) (на рис. 2.36 показан штрих-пунктиром) становится уже, чем спектр сигнала s(t), и при вычислении интеграла в выражении (2.125) пределы интегрирования должны быть — 2πf'_т, 2πf''_т вместо —2πf_т; 2πf_т. Коэффициенты с_п при этом являются уже выборками не заданного сигнала s(t), а некоторой другой функции s₁(t), спектр которой ограничен наивысшей частотой f"m.

Итак, сокращение интервалов между выборками по сравнению о величиной 1/2 f_m допустимо, но бесполезно. Увеличение же интер­вала сверх величины 1/2 f_m недопустимо.

Рассмотрим теперь случай, когда длительность сигнала s (t) конечна и равна Т_с, а полоса частот по-прежнему равна f_m. Эти условия, строго говоря, несовместимы, так как функция конечной длительности обладает теоретически бесконечно широким спектром. Практически, однако, всегда можно определить наивысшую частоту спектра f_m так, чтобы «хвосты» функции времени, обусловленные отсеканием частот, превышающих f_m, содержали пренебрежимо малую долю энергии по сравнению с энергией заданного сигнала s (t). При таком допущении, если имеется сигнал длительностью Т_с с полосой частот f_m, общее число независимых параметров [т. е. значений s (nΔt)],которое необходимо для полного задания сигнала, очевидно, будет равно

П ри этом выражение (2.120) принимает следующий вид (при отсчете времени от первой выборки):

Число N иногда называют числом степеней сво­боды сигнала s (0, так как даже при произвольном выборе зна­чений s (nΔt) сумма вида (2.127) определяет функцию, удовлетво­ряющую условиям заданного спектра и заданной длительности сиг­нала. Число N иногда называют также базой сигнала.

Энергию и среднюю мощность сигнала нетрудно выразить через заданную последовательность временньтх выборок.

Используя формулы (2.16) и (2.123), получаем

И з последнего выражения видно, что средняя за время Т_с мощность непрерывного сигнала равна среднему квадрату выборки. Усреднение производится по всем интервалам, число которых рав­но 2 f_mТ_с.