§ 2. Приложения определенного интеграла

2.1. Площадь фигуры. Система декартовых координат

Площадь криволинейной трапеции , ограниченной сверху графиком функции , слева и справа – прямыми и соответственно, снизу – осью (рис. 1), вычисляется по формуле

. (2.1)

Рис. 1	Рис. 2

Площадь криволинейной трапеции (рис. 2), ограниченной справа графиком функции , сверху и снизу – соответственно прямыми , , слева – осью , определяется формулой

. (2.2)

Площадь криволинейной фигуры , ограниченной сверху графиком функции , снизу – графиком функции , слева и справа – прямыми , (рис. 3), вычисляется по фор­муле

. (2.3)

Данная формула получена с помощью формулы (2.1), так как указан­ная фигура представляет собой разность двух криволинейных трапеций.

Рис. 3	Рис. 4

Площадь криволинейной фигуры , ограниченной слева и справа соот­ветственно графиками функций , , снизу и сверху – прямыми , (рис. 4), определяется формулой

. (2.4)

В общем случае криволинейную фигуру разбивают на час­ти, площади которых вычисляют по приведенным формулам или определяют непосредственно.

Если линия задана параметрическими уравнениями , , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми , и отрезком оси , выражается формулой

, (2.5)

где и – значения, между которыми изменяется параметр , когда точка пробегает слева направо всю линию, ограничивающую трапецию сверху. Значения и определяются из уравнений , ; при этом выполняется условие при .

Пример 2.1. Вычислить площадь сегмента, отсекаемого прямой от параболы .

Решение. Решая совместно систему

получаем координаты точек и (рис. 5): , . По формуле (2.4) находим, что

.

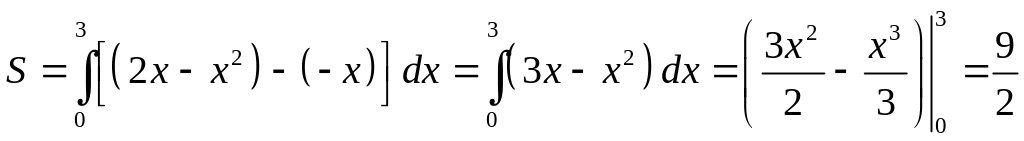Рис. 5	Рис. 6

Пример 2.2. Найти площадь фигуры, ограниченной параболами , .

Решение. Решая систему уравнений

найдем ординаты точек пересечения кривых , (рис. 6).

По формуле (2.4) имеем

.

Пример 2.3. Найти площадь фигуры, ограниченной линиями , и осью абсцисс.

Решение. По формуле (2.3) вычислим искомую площадь:

.

Пример 2.4. Найти площадь фигуры, ограниченной эллипсом:

; .

Решение. В силу симметрии эллипса достаточно найти площадь одной его четверти, а затем умножить результат на 4. Если изменяется в пределах от до , то параметр изменяется в пределах от до . По формуле (2.5) получим

Замечание. Когда , получаем – площадь круга радиуса R.

Найти площади фигур, ограниченных кривыми, заданными в прямоугольных координатах; в этом и следующих параграфах данного раздела все параметры считаются положительными:

2.1. , .	2.2. , , .
2.3. , .	2.4. , .
2.5. , , .	2.6. , , .
2.7. , .	2.8. , , .
2.9. , .

2.10. , , , , .

2.11. , , , .

2.12. , .

2.13. , , , .

2.14. , , , .

Найти площадь фигуры, ограниченной данной параболой и касательными к ней, проведенными в точках с абсциссами и , если:

2.15. , , .

2.16. , , .

2.17. Найти площадь фигуры, ограниченной осью абсцисс, кривой и касательной к ней, параллельной прямой .

2.18. Найти площадь фигуры, ограниченной параболой , касательной к ней в точке и осями координат.

Найти площади фигур, ограниченных кривыми, заданными параметрически:

2.19. , (циклоида) и .

2.20. , .

2.21. , (астроида).

2.22. , , (развертка круга) и , .

Найти площадь петли кривой, заданной параметрически:

2.23. , .

2.24. , .

Ответы: 2.1. . 2.2. . 2.3. . 2.4. . 2.5. . 2.6.  . 2.7.  . 2.8.  . 2.9. . 2.10. . 2.11. . 2.12.  . 2.13.  . 2.14. . 2.15. . 2.16. . 2.17.  . 2.18. . 2.19.  . 2.20. . 2.21. . 2.22. . 2.23. . 2.24.  .