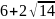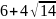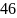АОО «Назарбаев Интеллектуальные школы»
Образец
Экзаменационная (письменная) работа по математике
итоговой аттестации выпускников старшей школы
Назарбаев Интеллектуальной школы
химико-биологического направления
2014-2015 учебного года
Структура письменной работы
В качестве измерителя уровня подготовки по математике выпускников старшей школы используются задания экзаменационной работы. Экзаменационная работа состоит из двух частей и содержит 18 заданий, которые различаются по содержанию, сложности и числу вопросов.
Часть 1 содержит 14 заданий базового уровня, они обозначены б1, б2, …, б14.
Задания Б1-Б10 – тестовые задания с выбором одного верного ответа из пяти предложенных.
Задания Б11-Б14 – задания открытого типа с кратким ответом.
Часть 2 содержит 4 заданий открытого типа с развернутым ответом продвинутого уровня, они обозначены п15, п16, п17, п18.
Система оценивания письменной работы
Максимальный балл за всю работу – 34 баллов.
Критерии оценивания заданий части 1
Правильное решение каждого из заданий Б1-Б10 части 1 оценивается 1 баллом, а заданий Б11-Б14 оцениваются 2 баллами.
Критерии оценивания заданий части 2
Полное и правильное решение каждого из заданий П15-П18 оценивается 4 баллами. Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, с необходимыми пояснениями и обоснованиями, полным, в частности, все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов. Полнота и обоснованность рассуждений оцениваются независимо от выбранного метода решения.
Шкала перевода баллов в оценку
-
Оценка «5»
Оценка «4»
Оценка «3»
Оценка «2»
90 – 100%
75 – 89%
51 – 74%
0 - 50%
31 - 34 б
26 - 30 б
18 - 25 б
0 - 17 б
Время выполнения работы – 240 минут или 4 часа.
Образец экзаменационной работы
Часть 1
Б1. Бассейн наполняется двумя трубами за 4 часа. Первая труба наполняет бассейн за 5 часов, тогда вторая труба наполняет бассейн:
за 15 часов
за 25 часов
за 10 часов
за 20 часов
за 30 часов
Б2.
На рисунке 1 показан график функции
.
Выберите правильный ответ:
«Значение а равно 5, а уравнение асимптоты равно х = 5»
«Значение а равно 5, а уравнение асимптоты равно х = 6»
«Значение а равно 6, а уравнение асимптоты равно х = 5»
«Значение а равно 6, а уравнение асимптоты равно х = 6»
«Значение а равно 5, а уравнение асимптоты равно у = 5»
Б3. В треугольнике АВС, площадь которого равна 12, проведена медиана АМ. На медиане взята точка К, АК:КМ = 1:2. Площади треугольников АВК и ВКМ соответственно равны:
1,5 и 3
2 и 6
2 и 3
2,5 и 4
2 и 4
Б4. Для транспортировки 45 тонн груза на 1300 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобиля для каждого перевозчика указана в таблице. Сколько тенге придется заплатить за самую дешевую перевозку?
Перевозчики |
Стоимость перевозки одним автомобилем (тенге на 100 км) |
грузоподъемность автомобилей (тонн) |
А |
3200 |
3,5 |
Б |
4100 |
5 |
В |
9500 |
12 |
А) 540800 тг
В) 520800 тг
С) 494000 тг
D) 485000 тг
E) 479700 тг
Б5.
Пусть
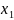и
– корни
квадратного уравнения
.
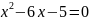Найдите
значение
выражения
.
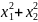Б6. Угол правильного п-угольника равен 1350. Найдите п.
16
14
12
10
8
Б7.
Найдите
значение
выражения
.
3
3
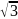
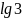
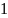
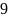
Б8.
К графику функции
проведена касательная, параллельная
прямой
.
Найдите
сумму
координат точки касания.
1,8
2
3
3,5
12
Б9.
Основанием пирамиды МАВС
служит прямоугольный треугольник АВС,
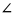С
=
900,
ВС
=
а,
А
=
300.
Боковые ребра пирамиды наклонены к
основанию под углом 600.
Каова
высота
пирамиды?
а
2а
а
а
Б10. Школьный оркестр состоит из учащихся средних и старших классов. 40% музыкантов мальчики, из них 30% из средних классов. 50% девочек также из средних классов. Какова вероятность того, что наугад выбранный музыкант окажется учащимся из средних классов?
0,41
0,42
0,43
0,5
0,53
Б11.
Пусть
,
,
,
,
.
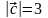Найдите
и
.
Ответ:
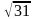см,
.
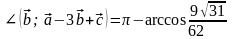Б12.
Закон движения точки по прямой задается
формулой
,
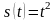где
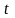– время
(в секундах),
– отклонение
точки в момент времени
(в метрах) от начального положения.
Найдите среднюю скорость движения точки
с момента
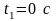до момента
.
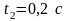Вычислите мгновенную скорость точки в
момент времени
.
Ответ:
,
.
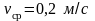Б13. На соревнованиях по кольцевой трассе один лыжник проходил круг на 2 мин быстрее другого и через час обошел его ровно на круг. За какое время каждый лыжник проходил круг?
Ответ: 10 мин, 12 мин.
Б14.
Найдите наименьшее и наибольшее значения
функции
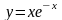на отрезке
.
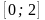Ответ:
,
.
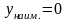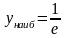Критерии оценивания заданий части 1
Правильное решение каждого из заданий Б1-Б10 части 1 оценивается 1 баллом, а заданий Б11-Б14 оцениваются 2 баллами.
Задания
|
Баллы
|
Б1 |
1 |
Б2 |
1 |
Б3 |
1 |
Б4 |
1 |
Б5 |
1 |
Б6 |
1 |
Б7 |
1 |
Б8 |
1 |
Б9 |
1 |
Б10 |
1 |
№ зада ния |
Критерии оценивания |
Баллы |
Максимальный балл |
Б11 |
Верно найдена длина вектора |
1 |
2 |
Верно найден угол между векторами |
1 |
||
Б12 |
Верно найдена средняя скорость |
1 |
2 |
Верно найдена мгновенная скорость |
1 |
||
Б13 |
Верно найдено время первого лыжника |
1 |
2 |
Верно найдено время второго лыжника |
1 |
||
Б14 |
Верно найдено наибольшее значение функции |
1 |
2 |
Верно найдено наименьшее значение функции |
1 |