
МЕТРОЛОГИЯ, ВЗАИМОЗАМЕНЯЕМОСТЬ, СТАНДАРТИЗАЦИЯ, СЕРТИФИКАЦИЯ ” Метрология
.pdf
Таблица 3 - Параметры соединений подшипника качения с отверстием в корпусе.
Наружное кольцо подшипника 90 l6 |
Отверстие в корпусе 90 H7 |
||
Основное отклонение “ l ” |
Основное отклонение “ Н ” |
||
|
|
||
es = 0 |
EI = 0 |
||
|
|
||
|
|
|
|
Td = JT6 =15 мкм |
TD = JT7 = 35 мкм |
||
ei = -15 мкм |
ES = +35 мкм |
||
|
|
|
|
Предельные размеры |
Предельные размеры |
||
|
|
|
|
dmin= 89,985 мм |
dmax= 90,000 мм |
Dmin= 90,000 мм |
Dmax= 90,035 мм |
|
|
|
|
Предельные значения зазоров и допуск посадки
Smax = 50 мкм, Smin = 0, ТS.= 50 мкм
11
3 Расчёт переходной посадки для соединения зубчатого колеса с валом.
Соединение зубчатого колеса с валом является ответственным, оно должно обеспечивать хорошее центрирование соединяемых деталей и в то же время достаточно лёгкую сборку-разборку соединения. Этим требованиям удовлетворяет переходная посадка
40 H7/k6, рекомендуемая для предпочтительного применения.
Величины допусков находятся по таблице стандарта ГОСТ 25346-89 в зависимости от
номинального размера и номера квалитета. Получим: TD = IT7 = 25 мкм и Td = IT6 = 16 мкм.
Определяются предельные отклонения: ei =+2 мкм, es = ei +Td = 2+16 = +18 мкм; EI =0, ES = EI +TD = 0+25 = +25 мкм.
Определяются предельные размеры вала и отверстия колеса:
d max |
d í |
es |
40 0 ,018 40 ,018ìì , d min d í ei 40 0 ,002 40 ,002 ìì ; |
Dmax |
Dí |
ES |
40 0 ,025 40 ,025 ìì , Dmin Dí EI 40 0 40 ìì . |
Поскольку выбранная посадка является переходной, то в соединениях деталей может быть получен либо зазор, либо натяг.
Определяются предельные значения натяга и зазора:
Smax = Dmax - dmin = 40,025 - 40,002 = 23 мкм, или Smax= ES-ei = 25-2 = 23 мкм Nmax = dmax - Dmin= 40,018 - 40 = 18 мкм, или Nmax= es - EI=18-0 = 18 мкм
Smin= Nmin = 0.
Определяется допуск посадки:
Tперех.пос = TS +TN = (Smax-Smin)+(Nmax-Nmin) = Smax+ Nmax= 23+18 =41 мкм..
Проверка: допуск любой посадки, в том числе и переходной, равен сумме допусков соединяемых деталей:
Tпос= TD+Td = 25+16 =41 мкм.
Полученные при анализе посадки данные приведены в таблице 4
12
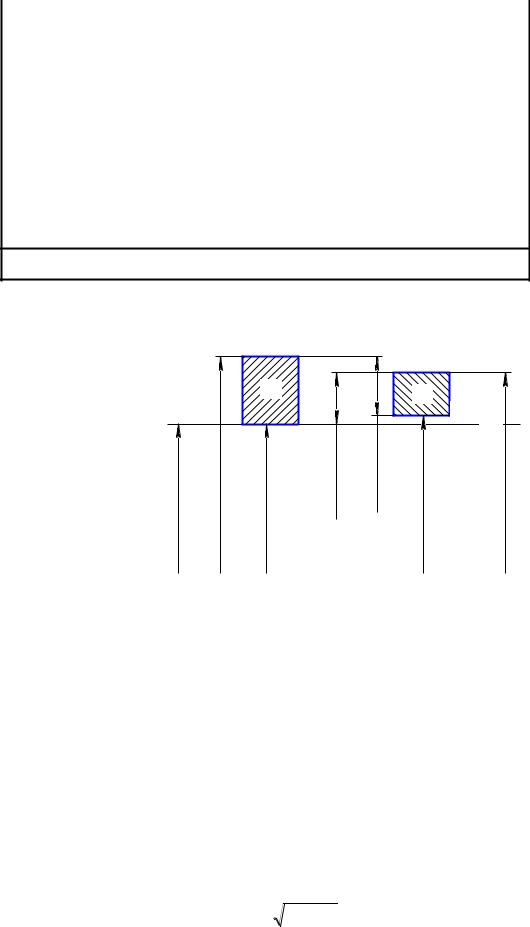
Таблица 4 - Результаты анализа переходной посадки 40 H7/k6
Отверстие 40 Н7 |
|
Вал 40 к6 |
|||
Основное отклонение “ Н ” |
Основное отклонение “ к ” |
||||
|
|
EI = 0 |
|
ei = +2 мкм |
|
|
|
|
|
||
TD = JT7 = 25 мкм |
Td = JT6 = 16 мкм |
||||
|
|
|
|
|
|
|
ES = +25 мкм |
|
es = +18 мкм |
||
|
|
|
|
||
Предельные размеры |
Предельные размеры |
||||
|
|
|
|
|
|
Dmin= 40,000 мм |
|
Dmax= 40,025 мм |
Dmin= 40,002 мм |
|
Dmax= 40,018 мм |
|
|
|
|
|
|
Предельные значения зазоров, натягов и допуск посадки
Smax= 23 мкм; Nmax= 18 мкм; Smin= Nmin= 0; Тпос.= 41 мкм
Расположение полей допусков представлено на рисунке 4. |
|
|
|||||
|
|
|
ES=+25 |
|
Smin =Nmin =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
es=+18 |
|
|
|
H7 |
|
k6 |
|
|
|
|
|
|
|
|
ei=+2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
EI=0 |
=23мкм |
|
=40,018мм |
0 |
|
|
|
|
|
||||
|
|
|
|
|
|||
=40мм |
=40,025мм |
=40мм |
=18мкм |
=40,002мм |
|
||
н |
|
||||||
=D |
|
||||||
н |
min |
max |
max |
min |
max |
|
|
d |
D |
N |
S |
d |
d |
|
|
|
max |
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
Рисунок - 4 Схема полей допусков переходной посадки 40 H7/k6
Определяется вероятность получения соединения с зазором и с натягом Построим схему полей допусков для рассчитываемой посадки с дополнительным
нанесением на ней кривых нормального распределения размеров отверстия и вала.
|
1 |
|
|
x 2 |
|
||
G |
e |
2 |
2 |
(1) |
|||
|
|||||||
2 |
|
||||||
|
|
|
|
|
|
||
Из теории вероятности известно, что сумма двух или нескольких независимых случайных величин, рассеивание которых подчиняется закону нормального распределения, тоже подчиняется этому закону.
Определяется среднее квадратичное отклонение суммарной совокупности:
|
S ,N |
|
2 |
2 |
, |
(2) |
|
|
D |
d |
|
|
13

где D , d - средние квадратичные отклонения независимых случайных величин,
находятся из правила 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Принимается TD = 6 D ,Td = |
6 d , определяются средние квадратичные отклонения для |
||||||||||||||||
отверстия и вала: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TD |
|
25 |
4.16 |
; |
|
|
|
Td |
|
|
16 |
2 ,66 |
||
|
D |
6 |
|
|
6 |
|
|
|
|
d |
6 |
|
6 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
S ,N |
4,16 2 |
2 ,66 2 |
4,947 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Строятся кривые нормального распределения сопрягаемых деталей и посадки. Максимум |
|||||||||||||||||
каждой кривой располагается на оси ординат. В нашем случае максимумы кривых располагают-
ся в середине полей допусков деталей и соответствуют отклонениям:
для отверстия D = 12,5 мкм., для вала d = 10 мкм.
Определяются наиболее вероятные размеры отверстий и валов и наиболее вероятных
значений зазоров или натягов:
Dнаиболее вероятный = 40,0125 мм dнаиболее вероятный = 40,0100 мм
x = Sнаиб.вероят = 40,0125 - 40,0100 = 0,0025 мм
Эти отклонения определяют посадку с зазором S = 2,5 мкм, являющуюся наиболее
вероятной. Следовательно, максимум кривой нормального распределения посадки должен соответствовать зазору S = 2,5 мкм. Для ее построения принимаем за нулевую линию схемы полей допусков ось ОУ, проходящую на расстоянии 2,5 мкм выше от оси (0-0) . Значения натягов условимся откладывать со знаком минус, т. е. вниз, а зазоров со знаком плюс. Тогда максимум кривой будет соответствовать значению х = 2,5
z=x/ S,N , |
(3) |
Построим кривую нормального распределения величин полученных зазоров или натягов.
Вероятность соединений с зазором определится как
PS 0 ,5 F (4)
Площадь F находим в зависимости от величины х (П7) z = 2,5 / 4,947 = 0,50
F = Ф (z) = Ф(0,50) = 0,1915;
РS = 0,5 + 0,1915 = 0,6915.
Вероятность получения соединения с натягом определяется как
14
|
|
|
PN |
1 PS 1 |
0 ,6915 0 ,3085 |
|
|
Таким образом, количество соединений с зазором - 69,15%,с натягом - 30,85%. |
|||||||
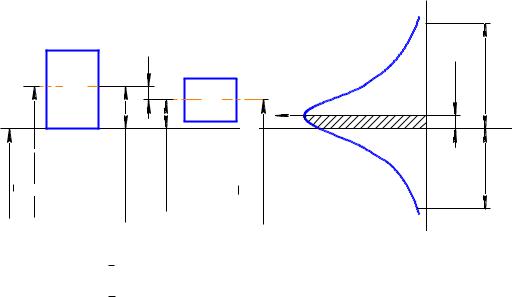
Кривая нормального распределения для посадки 40 H7/k6 представлена на рисунке 5. |
|||||||
|
|
|
|
|
+х(+z) |
|
|
|
+25 |
|
|
|
зазоры |
=23мкм |
|
|
|
|
|
|
|||
|
|
|
2 |
+18 |
х=2,5 |
||
|
TD |
|
|
||||
|
|
Td |
max |
||||
|
|
|
|
|
|
S |
|
0 |
|
|
|
+2 |
у |
0 |
|
|
|
|
0 |
||||
|
|
|
|
|
=18мкм |
||
=40мм |
|
D=12,5мкм |
d=10мкм |
|
|
||
D |
d |
натяги |
max |
||||
N |
|||||||
|
|||||||
|
|
|
|
|
-х(-z) |
|
|
|
|
d - наиболее вероятный диаметр вала, |
|
||||
D - наиболее вероятный диаметр отверстия.
Рисунок 5 - Кривая нормального распределения для посадки 40 H7/k6
15
5 Расчёт посадки с натягом для соединения венца зубчатого колеса со ступицей
Для соединения венца зубчатого колеса со ступицей принимается посадка с натягом,
которая применяется в неподвижных и редко разбираемых соединениях.
Цель расчет заключается в выборе посадок, обеспечивающих неподвижность соединения при действии внешних нагрузок и прочность сопрягаемых деталей. Исходя из первого условия
(неподвижность соединения) определяется минимальная величина натяга Nmin,, необходимая для восприятия и передачи внешних нагрузок. Исходя из второго условия (прочность сопрягаемых деталей) определяется максимальная допустимая величина натяга Nmax, при которой деформа-
ции сопрягаемых деталей, как правило, не выходят за пределы упругости.
При расчетах используются результаты решения задачи Ляме по определению напряжений и перемёщений в толстостенных полых цилиндрах.
Механические показатели материалов сопрягаемых деталей представлены в таблице 5.
Таблица 5 - Механические показатели материалов сопрягаемых деталей
Деталь |
Марка материала |
Т , МПа |
E, МПа |
μ |
f |
|
|
|
|
|
|
Ступица |
Сталь 45 ГОСТ 1050-88 |
650 |
2,1 Ĥ10 5 |
0,3 |
0,07 |
|
|
|
|||
Зубчатый венец |
Сталь 20ХНМ ГОСТ 4543-71 |
800 |
|
|
|
|
|
|
|
|
|
Определяется требуемое минимальное давление на контактных поверхностях соединения: 1. Из условия неподвижности соединения в зависимости от характера и величины
передаваемой нагрузки определяется требуемое минимальное давление на контактных поверхностях соединения.
а) при действии крутящего момента
p M кр |
|
2 M |
кр |
10 3 |
|
2 90 |
10 3 |
0 ,9135 МПа |
d |
|
l f |
3 ,14 160 2 |
35 0 ,07 |
||||
min |
|
2 |
|
|
б) при действии осевой системы силы
p Pос |
|
Pос |
|
|
20 |
|
0 ,0162 МПа |
|
|
|
|
||||
min |
|
d l f |
|
3 ,14 160 |
35 |
0 ,07 |
|
|
|
|
|||||
в) при совместном действии крутящего момента и осевой силы
p R |
R |
|
|
||
d l f |
||
min |
||
|
где R - равнодействующая сила при совместном нагружении соединения осевой силой и крутящим моментом;
d и l - номинальный диаметр и длина соединения, мм;
f - коэффициент трения на сопрягаемых поверхностях.
16

Определяется равнодействующая сила:
R |
2 М кр 10 3 2 |
2 |
|
|
2 90 10 |
3 2 |
20 |
2 |
1125 ,17 Н , |
|||||||
|
|
|
|
|
ос |
|
|
|
|
|
|
|||||
|
|
|
|
P |
|
|
|
|
|
|
|
|||||
|
|
d |
|
|
|
|
|
|
160 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
pmin |
|
|
|
1125 ,17 |
|
|
|
0 ,9136 МПа |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
3 ,14 |
160 |
|
35 |
0 ,07 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
По полученным значениям контактного давления, используя закон Гука и решение задачи Ляме, определяется величина наименьшего натяга Nmin расч , при котором будет обеспечена неподвижность соединения:
|
|
C |
D |
|
C |
d |
|
d |
10 3 , |
(5) |
|
N min расч |
pmin |
|
|
|
|||||||
|
|
E d |
|||||||||
|
|
E D |
|
|
|
|
|
||||
где ЕD и Еd - модули упругости материалов соединяемых деталей, МПа;
CD и Cd - коэффициенты Ляме.
Определяются коэффициенты Ляме:
|
|
|
|
|
|
d |
2 |
|
|
|
|
|
160 |
2 |
|
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
C D |
|
|
|
|
D0 |
|
|
|
D |
|
|
|
168 |
|
|
|
0 ,3 20 ,81 ; |
(6) |
||||||||||
|
|
|
|
d |
|
2 |
|
|
|
160 |
|
2 |
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
D0 |
|
|
|
|
|
|
|
|
168 |
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
d |
0 |
2 |
|
|
1 |
|
40 |
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
C d |
|
|
|
|
d |
|
|
d |
|
|
|
160 |
|
|
0 ,30 0 ,83 , |
(7) |
||||||||||||
|
|
|
d |
0 |
2 |
|
|
|
40 |
|
2 |
|
||||||||||||||||
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
160 |
|
|
|
|
||||||||||
где D0 = 168 - наружный диаметр охватывающей детали, мм;
d0 = 40 - диаметр внутренней полости охватываемой детали, мм;
μD и μd – охватывающие коэффициенты Пуассона.
N |
min расч |
0 ,9136 ( 20 ,81 |
2 ,1 10 5 |
0 ,83 |
2 ,1 10 5 ) 160 |
10 3 |
15 ,063 мкм . |
|
|
|
|
|
|
|
2. На основе теорий наибольших касательных напряжений определяется максимальное допустимое давление pmax, при котором отсутствуют пластические деформации соединяемых деталей:
а) для охватывающей детали:
|
|
|
|
|
|
d |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
pD 0 ,58 TD |
|
|
|
, |
(8) |
||||
|
|
|||||||||
|
|
|
|
|
D0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
160 |
2 |
|
|
|
|
|
pD |
0 ,58 800 |
1 |
|
|
43 ,14МПа |
|
||||
|
|
|
|
|||||||
|
|
|||||||||
|
|
|
|
168 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
17

б) для охватываемой детали:
|
|
|
|
|
|
|
d |
|
|
2 |
|
|
||
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
pd |
0 ,58 Td |
1 |
|
|
|
|
|
, |
(9) |
||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
d |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
40 |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
pd |
0 ,58 650 |
1 |
|
|
|
|
353 ,44МПа |
|
||||||
|
|
|||||||||||||
|
|
|
|
|
|
160 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где ТD и Тd -пределы текучести материалов охватывающей и охватываемой деталей,
МПа.
Лимитирующим фактором является прочность охватывающей детали. Поэтому в при
расчете наибольшего расчетного натяга используется значение РD max.
Определяется величина наибольшего расчетного натяга:
N |
max расч |
p |
D max |
( C |
D |
E |
D |
C |
d |
E |
d |
) d |
10 3 , |
(10) |
|
|
|
|
|
|
|
|
|
где - коэффициент учитывающий неравномерность распределения давления по поверхности сопряжения.
Принимается коэффициент = 0,9 [xx].
|
|
20 ,81 |
|
|
0 |
,83 |
|
|
|
|
3 |
|
N max расч |
43 ,14 0 ,9 |
|
|
|
|
|
|
|
160 |
10 |
|
640 ,15 мкм . |
2 ,1 10 |
5 |
2 ,1 |
10 |
5 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
3. Прежде чем осуществить выбор посадки на основе найденных величин Nmin расч и, Nmax расч
необходимо учесть, что при запрессовке будет происходить смятие неровностей на контактных поверхностях отверстия и вала, в результате чего фактическая величина натяга окажется меньше расчетной, определяемой как разность dизм и Dизм .
|
5 |
( R |
aD |
R |
ad |
) , |
(11) |
|||
ш |
|
|
|
|
|
|
||||
ш 5 |
( 0 ,8 0 ,8 ) |
8 мкм |
|
|||||||
Определяется минимальная и максимальная величины функциональных натягов с учетом |
||||||||||
поправки ш: |
|
|
|
|
|
|
|
|
|
|
N min функ |
N min расч |
ш , |
(12) |
|||||||
N max функ |
N max расч |
ш |
||||||||
|
||||||||||
N min функ |
15 |
,063 8 |
23 мкм |
|
||||||
N max функ |
640 ,15 |
8 |
648 мкм |
|
||||||
По ГОСТ 25364-88 и ГОСТ 2534-82 выбирается посадка, удовлетворяющая условиям |
|
|||||||||
N min ст N min функ и |
|
N max ст |
N max функ |
|
||||||
18
где Nmin ст и, Nmax ст - минимальное и максимальное значения натяга, обеспечиваемые какой-либо стандартной посадкой.
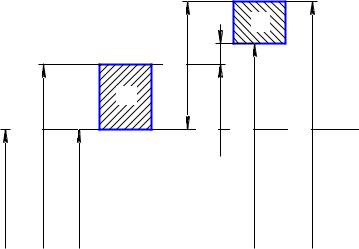
Принимается посадки в системе отверстия Н7/s6, которая обеспечит соединение гарантированным натягом, будет более экономичной и обеспечивать больший запас по прочности соединяемых деталей. Расположение полей допусков представлено на рисунке 6.
|
|
|
|
|
es=+125 |
|
|
|
|
=125мкм |
|
|
s6 |
|
|
ES=+40 |
|
|
ei=+100 |
|
|
|
|
|
|
||
|
|
|
|
мкм=60 |
|
|
|
|
H7 |
max |
|
=160,125мм |
|
|
=160,040мм |
N |
|
=160,100мм |
||
0 |
|
min |
||||
мм=160 |
|
|
N |
min |
max |
|
|
|
EI=0 |
|
|
|
0 |
н |
max |
=160мм |
|
|
d |
d |
=D |
D |
min |
|
|
|
|
d |
|
D |
|
|
|
|
н |
|
|
|
|
|
|
Рисунок 6 – Схема полей допусков для посадки с натягом 160 H7/s6
19
5 Выбор и анализ посадок для шпоночного соединения
Необходимо назначить посадку на шпоночный паз в соединении шпонка - вал и шпонка -
ступица колеса. Выбирается шпонка 12 8 40 ГОСТ 23360-78 [4].
Анализируя характер работы и условия сборки, выбирается нормальный тип соединения.
В этом случае для соединения шпонки с пазом вала выбирается посадка N9/h9, а для соедине-
ния шпонки с пазом ступицы – JS9/h9.
Рассчитывается посадка соединения шпонка-вал 12N9/h9 [8].
Определяются предельные отклонения:
ES = 0, EI = ES - IT = 0 – 43 = -43 мкм; es = 0, ei = es - IT = 0 – 43 = -43 мкм;
Определяются предельные размеры паза вала и шпонки:
D в |
D в ES |
12 |
0 |
12 мм , |
D в |
D в EI |
12 |
0 ,043 |
11 |
,957 мм ; |
||
max |
н |
|
|
|
|
min |
|
н |
|
|
|
|
d max |
d н |
es |
12 |
0 |
12 мм , d min |
d н |
ei |
12 |
0 ,043 |
11 |
,957 мм . |
|
Определяются предельные значения зазора и натяга:
N в |
d |
max |
D в 12 11 ,957 |
0 ,043 мм , S в |
D в |
d |
min |
12 |
11 ,957 |
0 ,043 мм , |
|||||||
max |
|
min |
|
max |
max |
|
|
|
|
|
|
||||||
N â |
S â |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
min |
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассчитывается посадка соединения шпонка-ступица 12Js /h9. |
|
|
|||||||||||||||
Определяются предельные отклонения: |
|
|
|
|
|
|
|
|
|
||||||||
EI |
IT |
|
43 |
21 ,5 |
ìêì , ES |
IT |
|
|
43 |
21 ,5 |
ìêì |
|
|
||||
|
|
|
|
|
|
||||||||||||
|
|
2 |
2 |
|
2 |
|
2 |
|
|
|
|
|
|
||||
Определяются предельные размеры паза ступицы: |
|
|
|
|
|
||||||||||||
D ст |
D ст |
ES 12 0 ,0215 |
12 ,0215 мм , D ст |
D ст |
EI |
12 0 ,0215 |
11 ,9785 мм ; |
||||||||||
max |
|
н |
|
|
|
|
min |
н |
|
|
|
|
|
|
|
||
Определяются предельные значения зазора и натяга:
N ст |
d |
max |
D ст |
12 |
11 ,9785 |
0 ,0215 мм , S ст |
D ст |
d |
min |
12 ,0215 |
11 ,957 |
0 ,0645 мм , |
max |
|
min |
|
|
max |
max |
|
|
|
|
||
N ñò |
S ñò |
0 . |
|
|
|
|
|
|
|
|
||
min |
|
min |
|
|
|
|
|
|
|
|
|
|
Предельные размеры параметров шпоночного соединения представлены в таблице 6 [1].
Таблица 6 - Предельные размеры основных геометрических параметров шпоночного соединения
Высота шпонки h, мм |
d-t1 |
d+t1 |
Длина шпонки |
Длина паза |
||
|
|
|
|
|
|
|
|
|
Предельные размеры, мм |
|
|||
|
|
|
|
|
|
|
8 |
-0,09 |
34,5 |
-0,2 |
43,3 +0,2 |
40 |
40 |
|
|
|
-0,620 |
-1 |
||
|
|
|
|
|
|
|
20
