§10.8. Ортогональные операторы
Определение 10.8.1. |
Линейный
оператор
|
,
действующий в евклидовом пространстве
E,
называется ортогональным
(или изометрическим),
если для
имеет место равенство
.
Из определения 10.8.1. следует, что ортогональный оператор сохраняет нормы элементов и величины углов между ними. Действительно,
где
- величина угла между элементами
и
,
а
- величина угла между элементами
и
.
Теорема 10.8.1. |
Ортогональный
оператор
имеет обратный
|
,
причем
.
|
Доказательство:
Для
по определению 10.8.1.
,
отсюда следует, что
|
или
.
Последнее равенство в силу леммы
10.6.1. означает, что
.
|
Из
равенства
Теорема доказана. |
вытекает, что
,
а из очевидного равенства
и теоремы 10.6.2. получаем, что
.
Наконец, по определению 8.2.8. получим
.
Следствие 10.8.1. |
Ортогональный оператор невырожденный. |
Следствие 10.8.2. |
В ортонормированном базисе матрица ортогонального оператора ортогональная. |
|
Доказательство:
Пусть оператор ортогональный. Тогда из соотношения , по теореме 10.8.1. и в силу §8.3.(4), в ортонормированном базисе справедливы равенства
Но
тогда
Следствие доказано. |
.
,
что и означает, согласно определению
5.1.4., ортогональность матрицы
.
В ряде приложений оказывается полезной
Теорема 10.8.2. (О полярном разложении) |
Любой
невырожденный линейный оператор
в E
может быть единственным образом
представлен в виде
|
,
где оператор
ортогональный, а оператор
-
самосопряженный и имеющий положительные
собственные значения.
|
Доказательство:
1.
Покажем вначале, что самосопряженный
оператор
(см. пример 10.7.1.) имеет только положительные
собственные значения. Действительно,
пусть
2.
Пусть
|
,
тогда, с одной стороны,
при
,
а с другой,
,
то есть
.
Но тогда все
в силу невырожденности
и определения скалярного произведения.
ортонормированный базис, состоящий
из собственных векторов
.
Рассмотрим множество элементов
.
Заметим, что
|
3.
Примем за искомый ортогональный
оператор
- оператор, переводящий ортонормированный
базис
в ортонормированный базис
Действительно,
во-первых, имеет место равенство
.
Во-вторых, из соотношений
4.
Покажем, наконец, единственность
разложения. Во введенных обозначениях
справедливо равенство
то, в силу самосопряженности , .
Предположим,
что существуют два различных
самосопряженных оператора
Заметим, что и по построению (см. 2.) имеют общую систему собственных векторов, а потому они коммутируют. Но тогда, согласно §8.2., справедливы равенства
Из
невырожденности и линейности
и
в силу теоремы 8.6.8. оператор
Теорема доказана. |
.
Но это означает, что
- также базис и притом ортонормированный.
,
и убедимся, что в качестве
можно взять оператор
.
следует, что базисные элементы
есть собственные векторы оператора
,
отвечающие положительным собственным
значениям
,
а значит, матрица
в базисе
диагональная и потому симметрическая.
Тогда, в силу леммы 10.7.1., оператор
самосопряженный.
,
поскольку из
и
следует, что
,
и
с положительными собственными
значениями такие, что
;
и
.
.
также невырожденный и поэтому из
равенства
следует
.
Таким образом,
-
самосопряженный оператор, определяемый
по
однозначно. Но
и, значит, также определяется однозначно
по
.
Замечания: 1. Теорема о полярном разложении является обобщением теоремы 5.5.2. о возможности представления аффинного преобразования плоскости в виде произведения двух операторов, первый из которых ортогональный, а второй - сжатие по двум взаимно перпендикулярным направлениям, матрица которого диагональная.
2. В случае вырожденного оператора разложение, аналогичное указанному в теореме 10.8.2., с неотрицательными собственными значениями самосопряженного оператора существует, но не единственно.
Задача 10.8.1. |
В
некотором ортонормированном базисе
в
|
линейный оператор
имеет матрицу
.
Найти его полярное разложение.
Решение:
1. Выполним искомое разложение по схеме, использованной в доказательстве теоремы 10.8.2. Матрица оператора в исходном ортонормированном базисе равна
.
Собственные значения и собственные векторы этого оператора равны соответственно
,
поэтому
(сохраняя обозначения, использованные
в доказательстве теоремы 10.8.2.) получим
для элементов, образующих ортонормированные
базисы
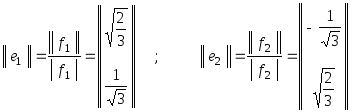
и
.
2.
Обозначив через
и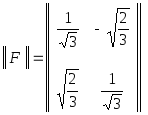
соответственно матрицы перехода от
исходного базиса к базисам
и
,
и рассуждая так же, как при решении
задачи 7.5.2., получим для матрицы
ортогонального оператора
выражение
.
Учитывая,
что матрица
ортогональная (как матрица перехода,
связывающая два ортонормированных
базиса), находим матрицу
,
которая в исходном ортонормированном базисе ортогональная.
3.
Поскольку
,
то
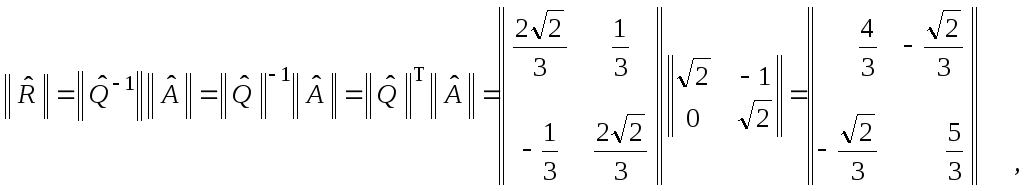
и, следовательно, искомое полярное разложение имеет вид
.
1) Обоснование существования такого разложения выходит за рамки данного курса. Здесь мы ограничимся рассмотрением лишь вопроса о его единственности.