
Шпора №2
.doc|
№22 Определение: два вектора называются коллинеарными, если они лежат на параллельных прямых. Определение: три вектора называются компланарными, если они лежат в параллельных плоскостях. Теорема: Если заданы два вектора a и b, причем а0 и эти векторы коллинеарны, то найдется такое действительное число , что b=a. В-ра бывают 3-х видов: свободные (можно перемещать куда угодно), скользящие (можно перемещать только вдоль линии,- приложение силы), связанные (нельзя перемещать никуда,- скорость точки) СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. Определение: скалярным произведением двух векторов называется произведение длин двух векторов на косинус угла между ними. (а,b)=|a| |b| cos u, u<90, пр-е полож.; u=90, пр-е =0; u>90, пр-е отриц. Свойства: (а,b)= (b,а) (а,b)= (а,b) (а+b,с)= (а,с)+ (b,с) (а,а)=|a|2 – скал.квадрат. Определение: два вектора называются ортогональными, когда скалярное пр-е равно 0. Теорема: Если векторы а и b заданы координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений соответствующих координат. A*B=x1*x2+y1*y2+z1*z2 Док-во: Разложим каждый в-р в ортогональном базисе: i, j, k: A=x1*i+y1*j+z1*k и перемножим,- там где в-ра перпендикулярны – произведение = 0. В итоге получим ф-улу
№23 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. Определение: векторным произведением двух векторов a и b обозначаемым [a,b] называется вектор с удовлетворяющий след. требованиям: 1. |c|=|a||b|sin u. 2. (с,а)=0 и (с,b)=0. 3. а, b, с образуют правую тройку. Свойства: [a,b]= - [b,a] [а,b]= [а,b] [a+b,c]=[a,c]+[b,c] [a,a]=0 Теорема: Длина векторного произведения векторов равна площади параллелограмма построенного на этих векторах. Доказательство: справедливость теоремы вытекает из первого требования определения векторного произведения. Теорема: Пусть векторы а и b заданы координатами в ортонормированном базисе, тогда векторное произведение равно определителю третьего порядка в первой строке которого наход-ся базисны векторы, во второй – координаты первого вектора, в третьей – координаты второго. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ: (A* B X C)=A*B*C = -B*A*C = C*B*A Смеш. Произведение равно объему параллепипеда, или 1/6 = объем пирамиды.
|
№24 Пусть задана система векторов а1, а2, а3,…,ал (1) одной размерности. Определение: система векторов (1) называется линейно-независимой, если равенство 1а1+2а2+…+лал=0 (2) выполняется лишь в том случае, когда все числа 1, 2,…, л=0 и R Определение: система векторов (1) называется линейно-зависимой, если равенство (2) выполнимо хотя бы при одном i0 (i=1,…,k) Свойства Если система векторов содержит нулевой вектор, то она линейно зависима Если система векторов содержит линейно-зависимую подсистему векторов, то она будет линейно-зависимой. Если система векторов линейно-независима, то и любая ее подсистема будет линейно независимой. Если система векторов содержит хотя бы один вектор, являющийся линейной комбинацией других векторов, то эта система векторов будет линейно зависимой. Теорема: Для того что бы два вектора были линейно-зависимы необходимо и достаточно, что бы они были коллениарны. Определение: два вектора называются ортоганальными, когда скалярное пр-е равно 0. Определение: вектор называется нормированным, если его скал.кв.равен 1. Определение: базис множества векторов называется ортонормированным, если все векторы базиса взаимно-ортагональны и каждый вектор нормирован. БАЗИС СИСТЕМЫ ВЕКТОРОВ. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ. 1. Определение: пусть задана некоторая система векторов. Базисом этой системы называется мах. совокупность линейно-независимых векторов системы. В множестве векторов на прямой базис состоит из одного ненулевого вектора. В качестве базиса множества векторов на плоскости можно взять произвольную пару. В множестве векторов в трехмерном пространстве базис состоит из трех некомпланарных векторов. 2. Прямоугольная (декартова) система координат на плоскости определяется заданием двух взаимно перпендикулярных прямых с общим началом и одинаковой масштабной ед. на осях. Прямоугольная (декартова) система координат в пространстве определяется заданием трех взаимно перпендикулярных прямых с общей точкой пересечения и одинаковой масштабной ед. на осях.
№29 Уравнение линии на плоскости Ф(x,y)=0 – Уравнение в самом полном виде Линия l представляет собой геометрическое место точек, координаты которых удовлетворяют условию y=f(x)
Пример в полярных координатах:
X=X(t) y=Y(t) t Є (-∞; +∞)
Как будто катится круг
|
№30
Определение:
Линия называется алгебраической,
если в некоторой декартовой
прямоугольной системе координатона
определялась уравнением Ф(x,
y) = 0,
Уравнение прямой линии на плоскости Утверждение: Если на плоскости П задана произвольная прямая l и зафиксирована произвольная декартова система координат Oxy, то прямая l определяется в этой системе координат уравнением первой степени.
Чтобы прямая l была осью X
Ах+By+C=0 , где A, B одновр.не равны нулю. Теорема: n(A,B) ортоганален прямой заданной ур-ем (1). Доказательство: подставим коорд. т.М0 в общее ур-е и получим Ах0+By0+C=0 (1’). Вычтем (1)-(1’) получим А(х-х0)+B(y-y0)=0, n(A,B), М0М(х-х0, y-y0). Слева в полученном равенстве записано скалярное произведение векторов, оно равно 0, значит n и M0M ортогональны. Т.о. n ортогонален прямой. Вектор n(A,B) называется нормальным вектором прямой. Замечание: пусть ур-я А1х+B1y+C1=0 и А2х+B2y+C2=0 определяют одну и ту же прямую, тогда найдется такое действительное число t, что А1=t*А2 и т.д. Определение: если хотя бы один из коэффициентов в ур-ии (1) =0, то ур-е называется неполным. 1. С=0, Ах+By=0 – проходит ч/з (0,0) 2. С=0, А=0, By=0, значит у=0 3. С=0, B=0, Ах=0, значит х=0 4. А=0, By+C=0, паралл. ОХ 5. B=0, Ах+C=0, паралл. OY
Точка пересечения прямых:
x1 y1 1 x - x2 y - y2 0 x2 y2 1 = x1- x2 y1- y2 0 = x- x2 y- y2 = 0 x3 y3 1 x2 y2 1 x1- x2 y1- y2
№31 Уравнения прямой 1) Общее ур-е прямой: Ах+By+C=0 (1), где A, B одновр.не равны нулю 2) Уравнение прямой в отрезках: x/a+y/b=1. Геом.смысл: прямая отсекает на осях координат отрезки а и b x-x1/e=y-y1/m Пусть на прямой задана точка и напр. вектор прямой (паралл.пр.). Возьмем на прямой произв. точки. q и M1М(х-х1; y-y1) x-x1/x2-x1=y-y1/y2-y1 Пусть на прямой даны две точки М1(x1;y1) и М2(x2;y2). Т.к. на прямой заданы две точки, то задан направляющий вектор q(x2-x1; y2-y1) y=kb+b. u – угол наклона прямой. Tg угла наклона называется угловым коэффициентом прямой k=tg u Пусть прямая задана в каноническом виде. Найдем угловой коэффициент прямой tg u = m/e. Тогда видим x-x1/e/e=y-y1/m/e. y-y1=k(x-x1) при y1-kx1=b, y=kx+b xcos+ysin-P=0 - угол между вектором ОР и положительным напр. оси ОХ.
№32 Угол между двумя прямыми в плоскости A1x + B1y + C1 = 0 A2x + B2y + C2 = 0 n1, n2 – 2 вектора этих прямых (n1, n2) = | n1| |n2| cos (n1, n2) = A1 A2+ B1 B2 - скалярное произведение
A1 A2 + B1 B2 A1 A2 + B1 B2 Угол между прямыми с угловым COS = —————— = —————— коэффициентом
| n1|
|n2| 1 tg φ2 - tg φ1 k2 – k1 перпендикулярность: k2= - — tg φ= —————— = ——— k1 1+ tg φ2 tg φ1 1+ k2 k1 |
|
№33 Расстояние от точки до прямой Если прямые выше L, то знак +, если ниже – то минус.
Площадь треугольника, заданного тремя точками: M1(x1, y1)
M2(x2,
y2)
M3(x3, y3)
№34 Линии второго порядка Эллипс. Эллипсом называется ГМТ, сумма расстояний которых от F1 до F2 есть постоянное число, которое мы обозначаем как 2a. r2+r1=2a;
x2c2+2a2xc+a4=a2(x2+2xc+c2+y2) x2(a2-c2)+a2y2=a2(a2-c2) Обозначим (a2-c2)=b2 x2b2+a2y2=a2b2
Уравнение Эллипса в параметрическом виде: sin2φ + cos2φ = 1 φ-параметр x=a•cosφ y=b•sinφ Дирректриссой эллипса, соответствующей данному фокусу F2 называется прямая D2 , перпендикулярная к фокальной оси и отстоящая от центра эллипса на расстояние a/e и лежащая по ту же сторону от центра эллипса что и фокус F2
ТЕОРЕМА ОБ ОТНОШЕНИИ РАССТОЯНИЙ. 2-ОЕ ОПРЕДЕЛЕНИЕ ЭЛЛИПСА Отношение расстояния любой точки эллипса до фокуса к расстоянию от нее до соответствующей директрисы есть величина постоянная равная е эллипса. Доказательство: r1/d1=e
Теорема: Эллипс
– ГМТ, удовлетворяющих условию:
Отношение расстояния от
Определение: эксцентриситет – величина равная отношению е=с/а;
|
№35 Линии второго порядка Гипербола. Определение: ГМТ на плоскости модуль разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная Каноническое уравнение: Будем считать, что фокусы гиперболы находятся на ОХ на одинаковом расстоянии от начала координат. |F1F2|=2c, М – произвольная точка гиперболы. r1, r2 – расстояния от М до фокусов; |r2-r1|=2a;
x2c2-2a2xc+a4=a2(x2-2xc+c2+y2) x2(a2-c2)+a2y2=a2(a2-c2) Обозначим (a2-c2)=b2 Нам нужно чтобы величина c2- a2 была положительная поэтому умнож. На (-1) a2y2 -x2(a2-c2) =a2(a2-c2) x2(a2-c2)-a2y2 =a2(a2-c2) Обозначим (a2-c2)=b2
Уравнение Гиперболы в параметрическом виде: sin2φ + cos2φ = 1 φ-параметр x=a•cosφ y=b•sinφ Дирректриссой гиперболы, соответствующей данному фокусу F2 называется прямая D2 , перпендикулярная к фокальной оси и отстоящая от центра гиперболы на расстояние a/e и лежащая по ту же сторону от центра гиперболы что и фокус F2 ТЕОРЕМА ОБ ОТНОШЕНИИ РАССТОЯНИЙ. 2-ОЕ ОПРЕДЕЛЕНИЕ ГИПЕРБОЛЫ Отношение расстояния любой точки гиперболы до фокуса к расстоянию от нее до соответствующей директрисы есть величина постоянная равная е эллипса. Доказательство: r1/d1=e
Теорема: Гипер-ла
– ГМТ, удовлетворяющих условию:
Отношение расстояния от
Определение: эксцентриситет – величина равная отношению е=с/а;
|
№36 Линии второго порядка Парабола. Определение: ГМТ на плоскости расстояние от которых до фиксированной точки на плоскости, называемой фокусом, равно расстоянию до фиксированной прямой этой плоскости называемой директрисой. Каноническое уравнение: Пусть фокус параболы находится на оси ОХ, а директриса расположение перпендикулярно оси ОХ, причем они находятся на одинаковом расстоянии от начала координат. |DF|=p, М – произвольная точка параболы; D – точка на директрисе; МF=r; MD=d;
№37 Кривые второго порядка на плоскости. Класс кривых, являющихся эллипсами кроме окружностей, параболами или гиперболами, могут быть определены по значению эксцентриситета: е<1 -эллипс (т.к. а>c) е=1 -парабола е>1 -гипербола (т.к. с>a) Общий вид кривой 2-ого порядка: a1x2+2a12xy+a22y2+2a13x+2a23y+a33=0
Определение: Инвариантой ур-я линии второго порядка относительно преобразования системы координат, называется функция зависящая от коэффициентов ур-я и не меняющая своего значения при преобразовании системы координат. Теорема: инвариантами уравнения линии второго порядка относительно преобразования системы координат являются следующие величины: I1; I2; I3 Вывод: при преобразовании системы координат 3 величины остаются неизменными, поэтому они характеризуют линию. Определение: I2>0 – эллиптический тип I1= a11+ a22 a11 a12 a13 I2<0 – гиперболический тип a11 a12 I3= a12 a22 a23 I2=0 – параболический тип I2= a12 a22 a13 a23 a33 ТЕОРЕМА О ЛИНИЯХ ЭЛИПТИЧЕСКОГО ТИПА. Теорема: Пусть задана линия элиптического типа т.е. I2>0 и пусть I1>0 следовательно уравнение (1) определяет: 1. I3<0 – эллипс; 2. I3=0 – точка; 3. I3>0 – ур-е не определяет. Если I3=0 говорят, что эллипс вырождается в точку. Если I3>0 говорят, что задается мнимый эллипс. ТЕОРЕМА О ЛИНИЯХ ГИПЕРБОЛИЧЕСКОГО ТИПА. Теорема: Пусть уравнение определяет линию гиперболического типа. Т.е. I2<0, I3≠0 - ур-е определяет гиперболу; I3=0 – пару пересекающихся прямых.
I
I3>0
Уравнение параболического типа
|
|
№38 Поверхность в 3-х мерном пространстве Поверхностью в 3-х мерном пространстве называется геометрическое место точек, удовлетворяющих уравнению F(x, y, z)=0 – поверхность в 3-х мерном пространстве. Пример: шар: x2 + y2 + z2 = a2 Линия Ф(x, y, z)=0 – л. пересечения 2-х плоскостей РАЗЛИЧНЫЕ УРАВНЕНИЯ ПЛОСКОСТИ. 1)Пусть задано трехмерное пространство. Теорема: Плоскость в афинной системе координат задается уравнением первой степени от трех переменных: Ax+By+Cz+D=0 (нормированное ур-е), где A,B,C≠0 одновременно. Справедлива и обратная теорема. Теорема: Вектор n(A, B, C) ортогонален плоскости, задаваемой общим уравнением. Вектор n – нормальный вектор плоскости. 2.
Уравнение
плоскости в отрезках:
3. Уравнение плоскости, определенной нормальным вектором и точкой. Пусть n(A,B,C) и М(x0;y0;z0). Запишем ур-е пл-ти: Ax+By+Cz+D=0 Ax0+By0+Cz0=-D A(x-x0)+B(y-y0)+C(z-z0)=0 4) Уравнение плоскости ч/з 3 точки. Пусть известны три точки не принадл. одной прямой. М1(x1;y1;z1); М2(x2;y2;z2); М3(x3;y3;z3) Пусть М(x;y;z) – произвольная точка плоскости. Т.к. точки принадл. одной плоскости то векторы компланарны. М1М x-x1 y-y1 z-z1 М1М2 x2-x1 y2-y1 z2-z1 =0 М1М3 x3-x1 y3-y1 z3-z1
Пусть плоскость определена точкой и парой некомпланарных векторов. V(V1;V2;V3); U(U1;U2;U3); M0(x0;y0;z0), тогда плоскость имеет вид: система: x=x0+V1t+U1s y=y0+V2t+U2s z=z0+V3t+U3s РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ. Ax+By+Cz+D=0; M0(x0;y0;z0)
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ. Угол между плоскостями: пусть заданы две плоскости: A1x+B1y+C1z+D1=0; A2x+B2y+C2z+D2=0, поэтому n1(A1;B1;C1); n2(A2;B2;C2). Отыскание угла между плоскостями сводится к отысканию его между нормальными векторами.
A1 B1 C1 A2 B2 C2 1) Если ранг равен 2, то плоскости пересекаются 2) Если ранг равен 1, то плоскости пересекаются 3) Если ранг расширенной матрицы =1, а основ- A1 B1 C1 D1 A2 B2 C2 D2 =1 |
№39 Уравнение прямой в пространстве (линия пересечения 2-х плоскостей)
1) Есть точка
M(x0,
y0,
z0)
и вектор a‾{a1,
a2,
a3}
Тогда прямая, проходящая через M
и параллельная a‾:
Это каноническое уравнение прямой в пространстве
i j k n3 = [n1 x n2] = A1 B1 C1 = B1 C1 i - A1 C1 j + A1 B1 k A2 B2 C2 B2 C2 A1 C1 A2 B2 a1 a2 a3
x=x0+at
y=y0+at z=z0+at
M1(x1,
y1,
z1)
M2(x2, y2, z2)
|
№40 Взаимное расположение прямой и плоскости Ax+By+Cz+D=0
Aa1 + Ba2 + Ca3≠0 Ax1+By1+Cz1+D≠0 - условия параллельности прямой и плоскости
Aa1 + Ba2 + Ca3=0 Ax1+By1+Cz1+D=0
Ее направленный вектор коллинеарен вектору нормали плоскости
№41 Поверхности второго порядка Эллипсоид (дыня) a11x2 + a22y2 + a33z2 + 2a12xy + 2a13xz + 2a23yz + a33 = 0 Каноническое уравнение:
На сечении всегда будет эллипс; a, b и с – расстояния от центра Конуса второго порядка
Цилиндрические поверхности
F(x,
y)=0
|
|
№42 Поверхности второго порядка. Гиперболоиды.
На сечении – эллипс. Если X=0 (продольное сечение), то будет гипербола
3) Эллиптический параболоид (полдыни):
Гиперболический параболоид (седло):
|
№28 Преобразование декартовых координат на плоскости Линейное ортогональное преобразование
Если выполняется – то ортогональное преобразование x = x1cosφ – y1sinφ y = x1cosφ – y1sinφ Теорема: при ортогональных преобразованиях сохраняется расстояние между точками. Док-во: M’1M’2 – расстояния между точками в новой сист. |M’1M’2|2 = |X’1 –X’2|2 + |Y’1-Y’2|2 = (a11x2 + a12y2 – a11x1 – a12y1 )2 +(a21x2 + a22y2 – a21x1 – a22y1 )2 = [a11(x2 – x1) + a12(y2 – y1)]2 + [a21(x2 – x1) + a22(y2 – y1)]2 = a211(x2 – x1)2 + a212(y2 – y1)2 + 2a11a12 (x2 – x1) (y2 – y1) + a221(x2 – x1)2 + a222(y2 – y1)2 + 2a21a22 (x2 – x1) (y2 – y1) = (a211+ a212) (x2 – x1)2 +(a212+ a222) (y2 – y1)2+2(x2 – x1) (y2 – y1)( a11a12 + a21a22 ) = |X’1 –X’2|2 + |Y’1-Y’2|2 Ч.Т.Д.
|
№28 Преобразование декартовых координат на плоскости Линейное афинное преобразование Преобразование на плоскости есть применение преобразований параллельного переноса и поворота. Пусть две прямоугольные системы координат имеют общее начало. Рассмотрим все возможные скалярные произведения базисных векторов: i1 = a11i + a12j | xi i1 = a21i + a22j | xj cos(i11i) = a11*1 + a12*0 cos(j1i) = a21; a21= cos(П/2 - φ) = -sinφ cos(i1j) = a12; a12= cos(П/2 - φ) = sinφ a22= cos(j1j) = cosφ Отсюда получаем: x=a + x1cosφ – y1sinφ y=b + x1sinφ – y1cosφ - формулы поворота системы координат на угол φ x=a + x1 y=b + y1 - формулы параллельного переноса. x1 = a11x + a12y + a13 a11 a12 y1 = a21x + a22y + a23 ▲= a21 a22 =0 Если ▲=0, система называется вырожденной. Линейное преобразование невырожденной с.к. называется АФФИННЫМ. Св-ва аффинного преобразования:
y = y1 также аффинное преобразование
|

 Пример в Декартовых
координатах: (x-a)2
+ (y-b)2
= R2
Пример в Декартовых
координатах: (x-a)2
+ (y-b)2
= R2
 Параметрическое
представление линии:
Параметрическое
представление линии:
 X=R(
t- sint)
Y=R(1- cost)
– уравнение Циклоида
X=R(
t- sint)
Y=R(1- cost)
– уравнение Циклоида


 Док-во: введем
произвольную систему координат,
Док-во: введем
произвольную систему координат,

 точки
М до произвольно выбранного фокуса
F2 кривой к
расстоянию от точки М до соответствующей
этому фокусу дирректриссе – есть
величина постоянная и равная e.
точки
М до произвольно выбранного фокуса
F2 кривой к
расстоянию от точки М до соответствующей
этому фокусу дирректриссе – есть
величина постоянная и равная e.
 точки
М до произвольно выбранного фокуса
F2 кривой к
расстоянию от точки М до соответствующей
этому фокусу дирректриссе – есть
величина постоянная и равная e.
точки
М до произвольно выбранного фокуса
F2 кривой к
расстоянию от точки М до соответствующей
этому фокусу дирректриссе – есть
величина постоянная и равная e.
 Уравнение
параболы в полярной системе координат
Уравнение
параболы в полярной системе координат 3=0
3=0
 бычная
гипербола
бычная
гипербола


 ной
=2, то плоскости совпадают
ной
=2, то плоскости совпадают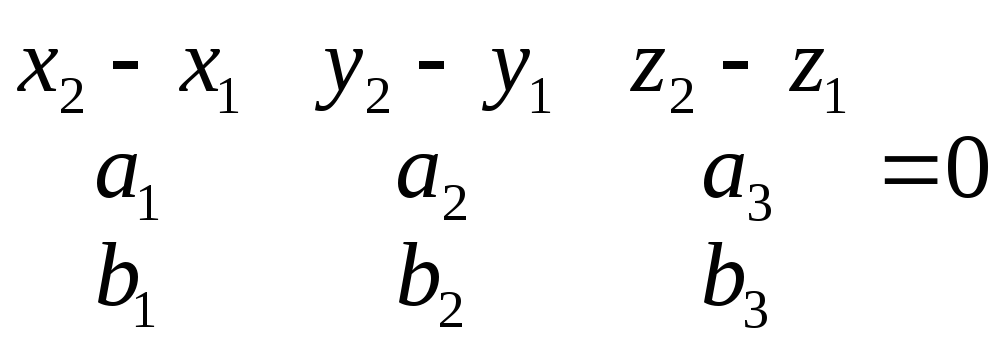

 Если
a=b,
- z=const
– в сеч. Окр.
Если
a=b,
- z=const
– в сеч. Окр.