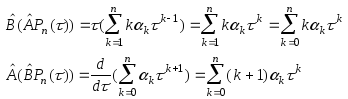Раздел 8 221

Определение

8.1.1.

Пусть каждому элементу x линейного пространства поставлен в соответствие единственный элементy линейного пространства . Тогда говорят, что в заданоператор, действующий в и имеющий значения в , обозначаемый .

При этом элемент y называется образом элемента x, а элемент x - прообразом элемента y.

Определение

8.1.2.

Оператор называется линейным, если для любых и любого числа имеют место равенства:

1. и

2. .

Пример

8.1.1.

1. В пространстве 2-мерных векторов линейным оператором является правило

,

связывающее вектор-прообраз с вектором-образом.

2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого пространства его производную функцию.

3. В пространстве многочленов линейным оператором является операция умножения многочлена на независимую переменную .

Задача

8.1.1.

Доказать, что операторы в примерах 1, 2 и 3 являются линейными.

Задача

8.1.2.

Является ли линейным оператор , ставящий каждому элементу в соответствие фиксированный элемент?

Решение:

Если , то- линейный оператор, действующий в.

Определение

8.2.1.

Линейные операторы иназываютсяравными, если . Равенство операторов обозначается как .

Суммой линейных операторов иназывается оператор, обозначаемый, ставящий каждому элементу линейного пространства в соответствие элемент .

Лемма

8.2.1.

Сумма двух линейных операторов является линейным оператором.

Доказательство:

Пусть и ;- числа, а , тогда

Лемма доказана.

Определение

8.2.2.

Нулевым оператором называется оператор, ставящий каждому элементу линейного пространства в соответствие нулевой элемент этого линейного пространства.

Определение

8.2.3.

Оператором, противоположным оператору , называется оператор, обозначаемый , ставящий каждому элементу линейного пространства в соответствие элемент .

Определение

8.2.4.

Произведением линейного оператора на число называется оператор, обозначаемый , ставящий каждому элементу линейного пространства в соответствие элемент .

Лемма

8.2.2.

Произведение линейного оператора на число является линейным оператором, для которого выполняются соотношения

Доказательство:

Утверждение леммы проверяется непосредственно. Например, для третьего равенства имеем .

Теорема

8.2.1.

Множество всех линейных операторов, действующих в линейном пространстве , является линейным пространством.

Доказательство:

Следует из определений 7.1.1., 8.2.1.-8.2.4. и лемм 8.2.1., 8.2.2.

Определение

8.2.5.

Произведением линейных операторов иназывается оператор, обозначаемый, ставящий каждому элементу линейного пространства в соответствие элемент .

Теорема

8.2.2.

Произведение линейных операторов является линейным оператором, для которого справедливы соотношения

Доказательство:

Докажем вначале линейность произведения линейных операторов.

Действительно

.

Проверим теперь сочетательный закон для произведения линейных операторов. Имеем

,

но, с другой стороны,

,

что и требовалось показать. Остальные утверждения теоремы проверяются аналогично.

Теорема доказана.

Замечание:

в общем случае произведение линейных операторов не обладает перестановочным свойством (или, иначе говоря, операторы не коммутируют), то есть, .

Определение

8.2.6.

Оператор называетсякоммутатором операторов и.

Задача

8.2.1.

В линейном пространстве алгебраических многочленов найти коммутатор для операторов: , ставящего в соответствие многочлену его производную функцию, и - оператора умножения многочлена на независимую переменную.

Решение:

Построим оператор . Для любого имеем:

Откуда получаем

и окончательно

.

Следовательно, данные линейные операторы не коммутируют.

Определение

8.2.7.

Оператор называетсяединичным (или тождественным) оператором, если каждому элементу линейного пространства он ставит в соответствие тот же самый элемент, то есть.

Определение

8.2.8.

Оператор называетсяобратным оператору и обозначается, если.

Пример

8.2.1.

В линейном пространстве функций , имеющих напроизводную любого порядка и удовлетворяющих условиям, оператор дифференцированияи- оператор интегрирования с переменным верхним пределом, являются взаимно обратными.

Действительно,

и

.

Замечания:

1. Не для всякого линейного оператора существует обратный оператор. Например, нулевой оператор не имеет обратного. Действительно, пустьпри всех, тогда для любогоимеет место, и, следовательно, равенствоне выполняется ни при каком.

2. Обратный оператор, если существует, то единственен. (Покажите это самостоятельно, использовав как аналог доказательство леммы 5.1.1.)

3. В случае бесконечномерного линейного пространства из условия может не следовать выполнение условия, что имеет, например, место в пространстве многочленовдля пары операторови, гдеесть оператор умножения многочлена на независимую переменную, а оператормногочленуставит в соответствие многочлен.