
- •Раздел 8 221
- •Раздел 8
- •§8.1. Линейные операторы
- •§8.2. Действия с линейными операторами
- •§8.3. Координатное представление линейных операторов
- •§8.4. Область значений и ядро линейного оператора
- •§8.5. Инвариантные подпространства и собственные векторы
- •§8.6. Свойства собственных векторов и собственных значений
- •§8.7. Линейные функционалы
§8.5. Инвариантные подпространства и собственные векторы
|
Определение 8.5.1. |
Подпространство
|
|
Пример 8.5.1. |
1 |
z
O y x
Рисунок 8.5.1. |
|
|
2.
Для оператора дифференцирования в
линейном пространстве функций f()
, имеющих на
|
|
Теорема 8.5.1. |
Матрица
линейного оператора
когда
линейная оболочка подмножества
базисных элементов
|
|
|
Доказательство:
Докажем
достаточность. Пусть матрица оператора
Иначе
говоря, если
|
|
|
Из
теоремы 7.4.1. следует, что
|
|
|
Докажем
необходимость. Пусть
Тогда
образ любого, в том числе и базисного,
элемента, принадлежащего
и, в сочетании с определением 8.3.1. доказывает необходимость.
Теорема доказана. |
|
Задача 8.5.1. |
Показать,
что всякое инвариантное подпространство
невырожденного линейного оператора
|
|
Решение:
|
Пусть
Если
оператор
|
Рассмотрим теперь условия, при которых у линейного оператора есть одномерное инвариантное подпространство.
|
Определение 8.5.2. |
Ненулевой
элемент
|
Замечание о важности собственных векторов
Допустим,
что для некоторого линейного оператора
![]() ,
заданного в
,
заданного в
![]() ,
удалось найтиn
линейно независимых собственных векторов
,
удалось найтиn
линейно независимых собственных векторов
![]() .
Это означает, что выполнены равенства
.
Это означает, что выполнены равенства![]() .
.
Приняв
эти элементы за базис, исходя из
определения 8.3.1., можно заключить, что
матрица линейного оператора
![]() в этом базисе будет иметь диагональный
вид
в этом базисе будет иметь диагональный
вид
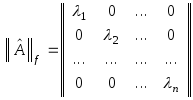 ,
,
для которого исследование свойств этого оператора существенно упрощается.
|
Задача 8.5.2. |
Показать,
что, если линейный оператор
|
|
Решение:
|
По
условию
|
Вычисление собственных векторов и собственных значений линейного оператора
Выберем
в
![]() некоторый базис
некоторый базис
![]() ,
в котором разложение элемента
,
в котором разложение элемента
![]() будет
будет![]() .
Пусть имеется линейный оператор с
матрицей
.
Пусть имеется линейный оператор с
матрицей![]() в этом базисе.
в этом базисе.
Равенство
![]() в координатной форме в
в координатной форме в![]() имеет вид
имеет вид![]() ,
то есть
,
то есть
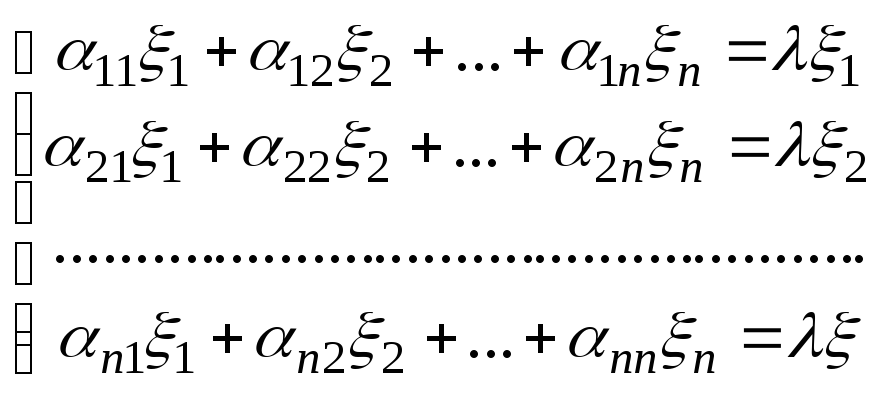 или
или
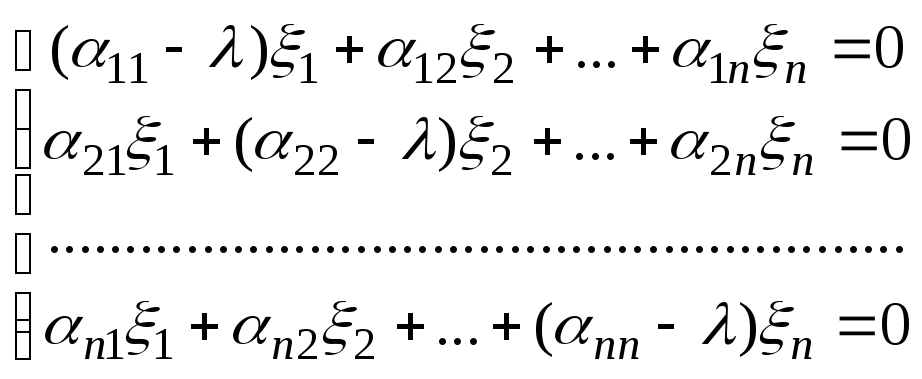 (8.5.1.)
(8.5.1.)
Поскольку собственный вектор должен быть ненулевым по определению, то нас интересуют только нетривиальные решения системы (8.5.1.), необходимым условием существования которых, согласно следствию 6.7.2., является равенство нулю определителя основной матрицы системы (8.5.1.) Таким образом, мы приходим к условию, которому должны удовлетворять собственные значения данного линейного оператора
![]() или
же
или
же
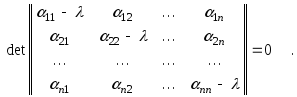 (8.5.2.)
(8.5.2.)
|
Определение 8.5.3. |
Уравнение
|
|
Теорема 8.5.2. |
Характеристический
многочлен линейного оператора не
зависит от выбора базиса в
|
|
|
Доказательство:
Заметим,
что оператор
Теорема доказана. |
Характеристическое уравнение является алгебраическим уравнением n-й степени относительно , что следует из определения детерминанта 6.1.2. и формулы (8.5.2.).
Решив
характеристическое уравнение (8.5.2.), из
однородной системы уравнений (8.5.1.) можно
найти собственные векторы, соответствующие
последовательно подставляемым в основную
матрицу этой системы найденным собственным
значениям. Примеры использования данного
алгоритма в
![]() иллюстрируют решения задач 8.6.1. и 8.6.2. В
случае же линейных пространств, не
имеющих базиса, задача отыскания
собственных значений и построения
собственных векторов может оказаться
значительно сложнее. Например, в линейном
пространстве функций, имеющих на
некотором интервале производную любого
порядка, линейный оператор дифференцирования
имеет бесконечно много собственных
векторов вида
иллюстрируют решения задач 8.6.1. и 8.6.2. В
случае же линейных пространств, не
имеющих базиса, задача отыскания
собственных значений и построения
собственных векторов может оказаться
значительно сложнее. Например, в линейном
пространстве функций, имеющих на
некотором интервале производную любого
порядка, линейный оператор дифференцирования
имеет бесконечно много собственных
векторов вида
![]() (где
- произвольная ненулевая константа) и
соответствующих им собственных значений
,
находимых из дифференциального уравнения
(где
- произвольная ненулевая константа) и
соответствующих им собственных значений
,
находимых из дифференциального уравнения
![]() .
.

 .
Множество радиус-век- торов точек
некоторой прямой на плоскости
.
Множество радиус-век- торов точек
некоторой прямой на плоскости
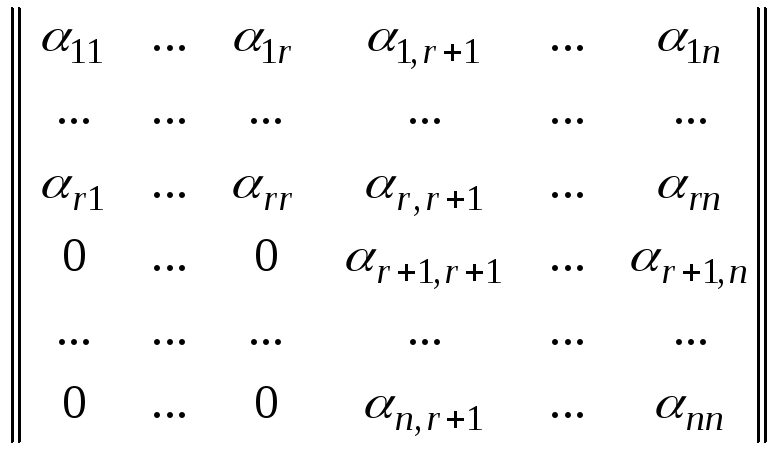
 ,
,