Б) Применить признак Лейбница (12 неделя)
1 |
|
|
14 |
|
|
2 |
|
|
15 |
|
|
3 |
|
|
16 |
|
|
4 |
|
|
17 |
|
|
5 |
|
|
18 |
|
|
6 |
|
|
19 |
|
|
7 |
|
|
20 |
|
|
8 |
|
|
21 |
|
|
9 |
|
|
22 |
|
|
10 |
|
|
23 |
|
|
11 |
|
|
24 |
|
|
12 |
|
|
25 |
|
|
13 |
|
|
|
|
|
Найти интервалы сходимости (радиус сходимости) и определить тип сходимости на концах интервала сходимости данных рядов. (13 неделя)
-
1
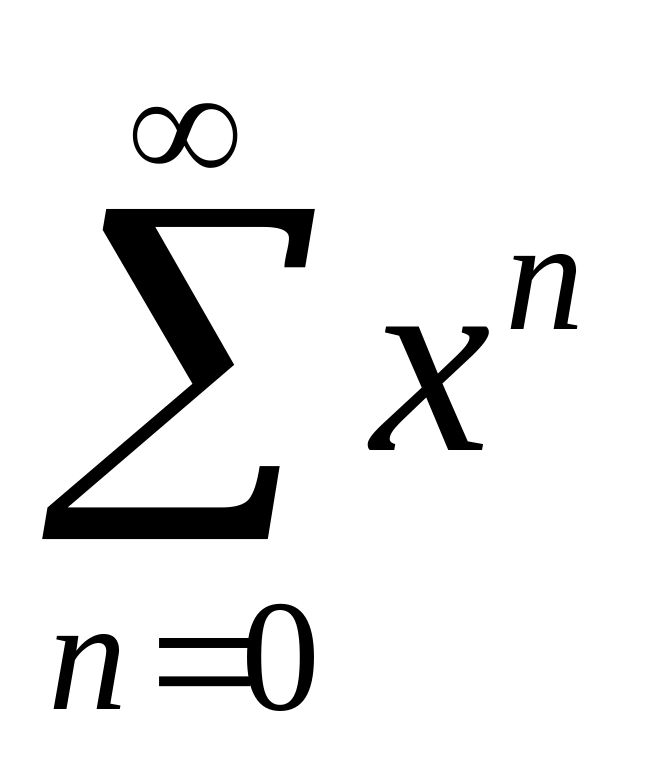
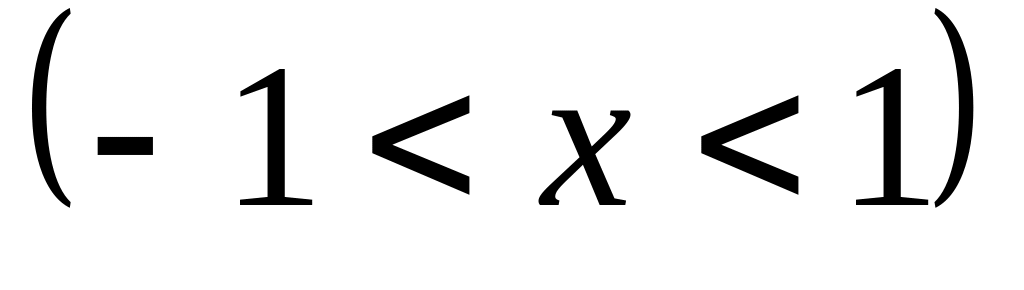
2
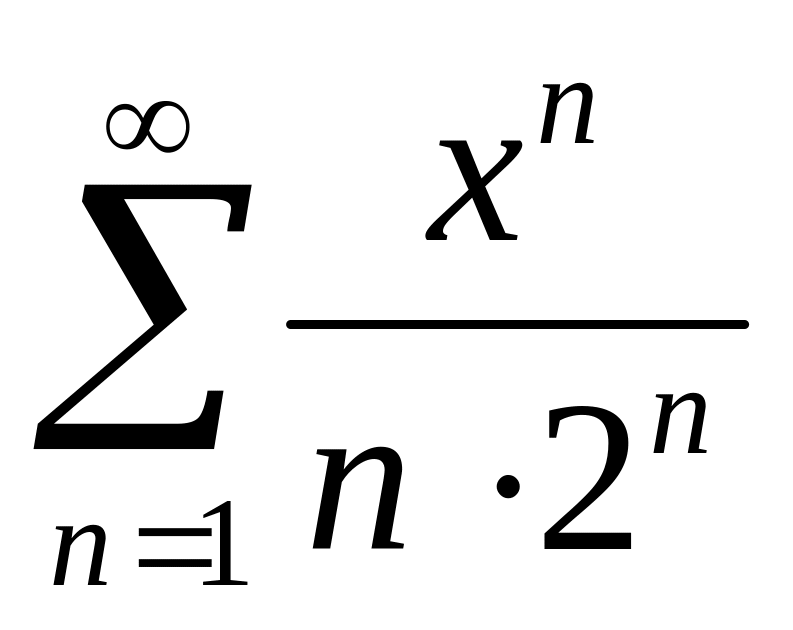
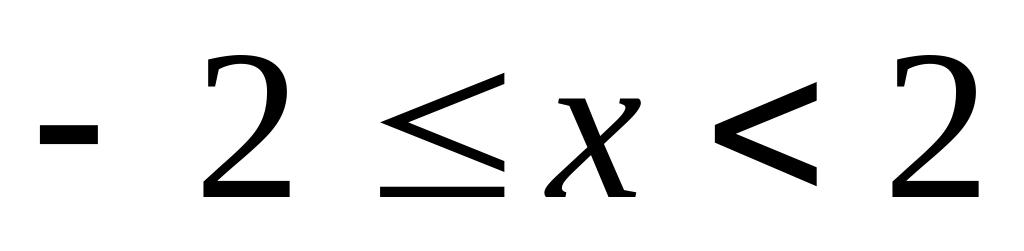
3
4
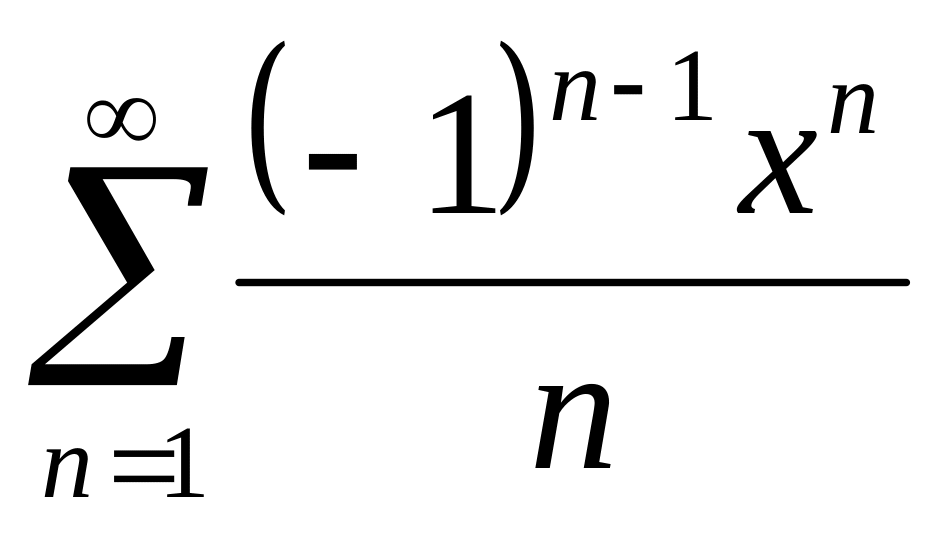
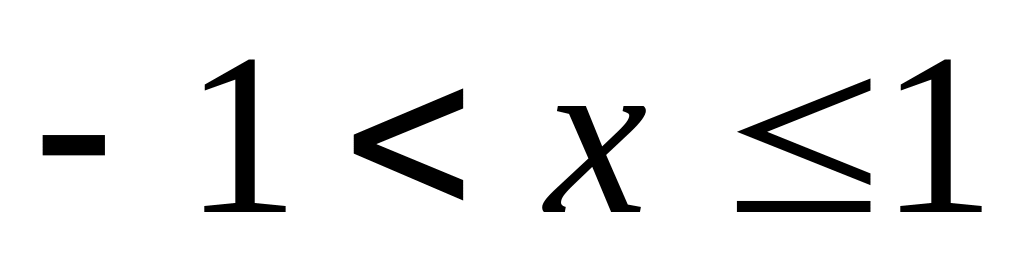
5
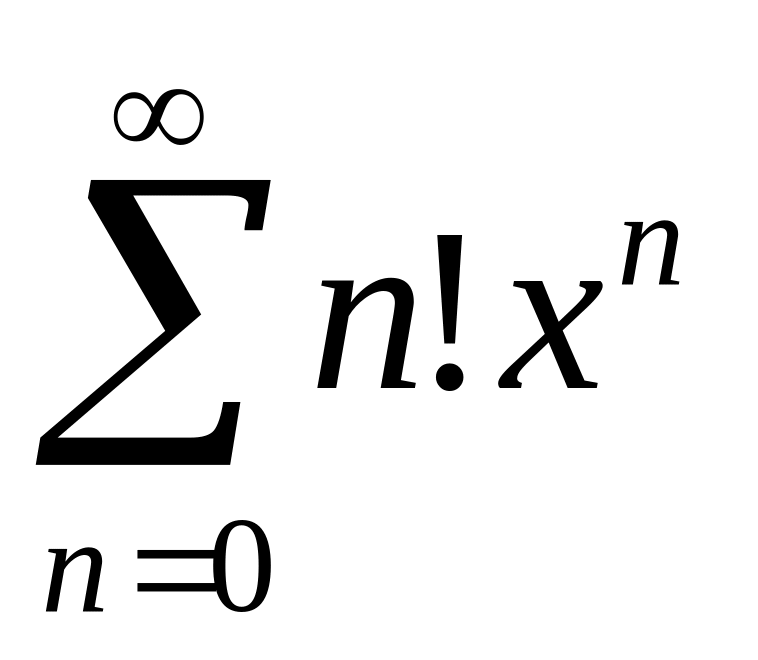
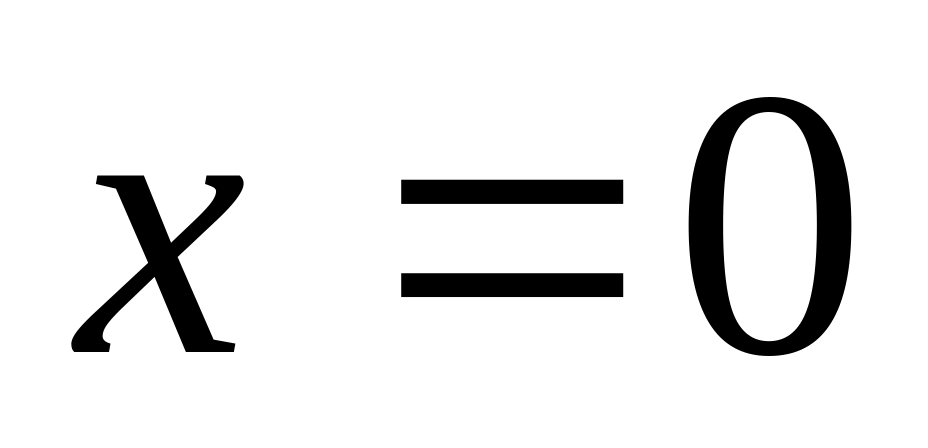
6
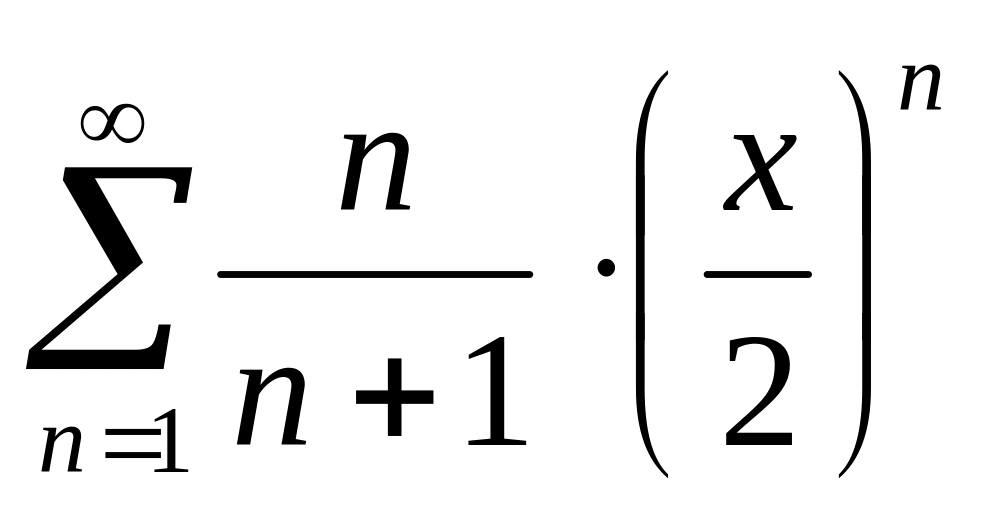
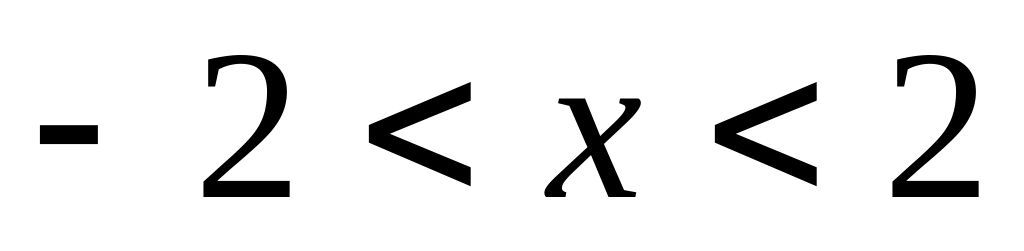
7
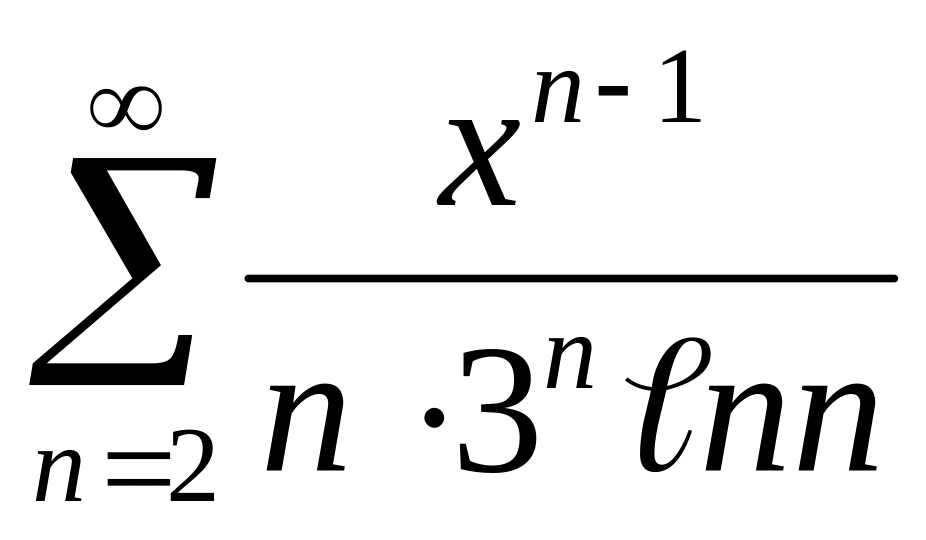
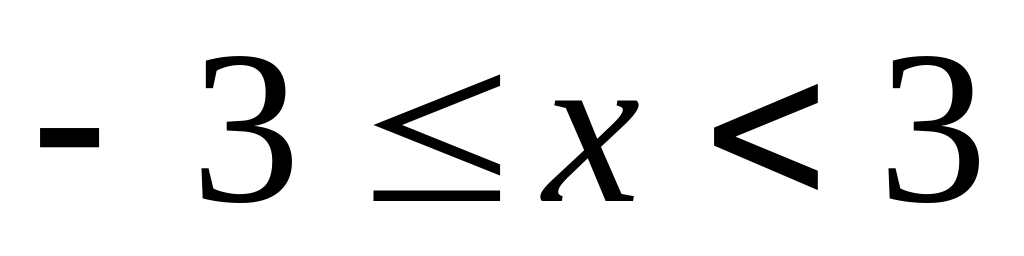
8
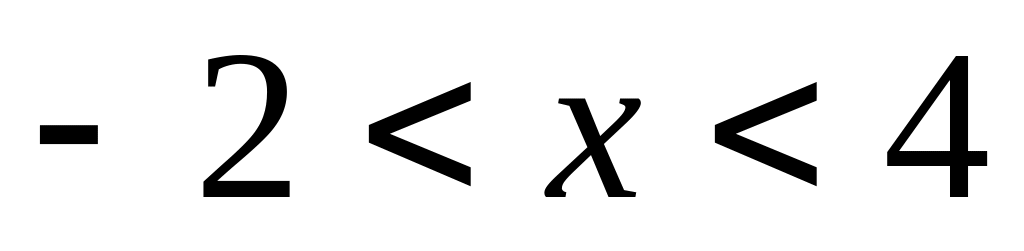
9
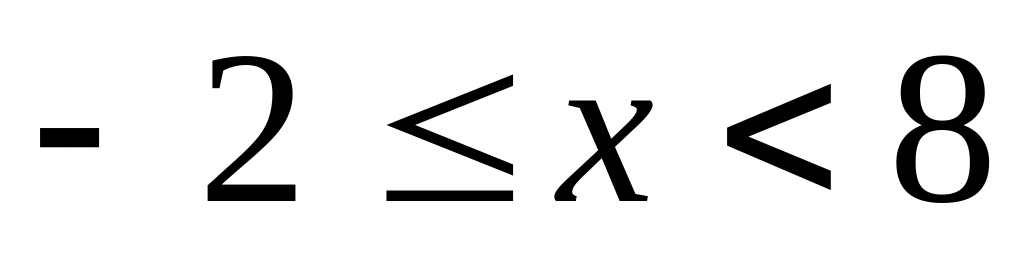
10
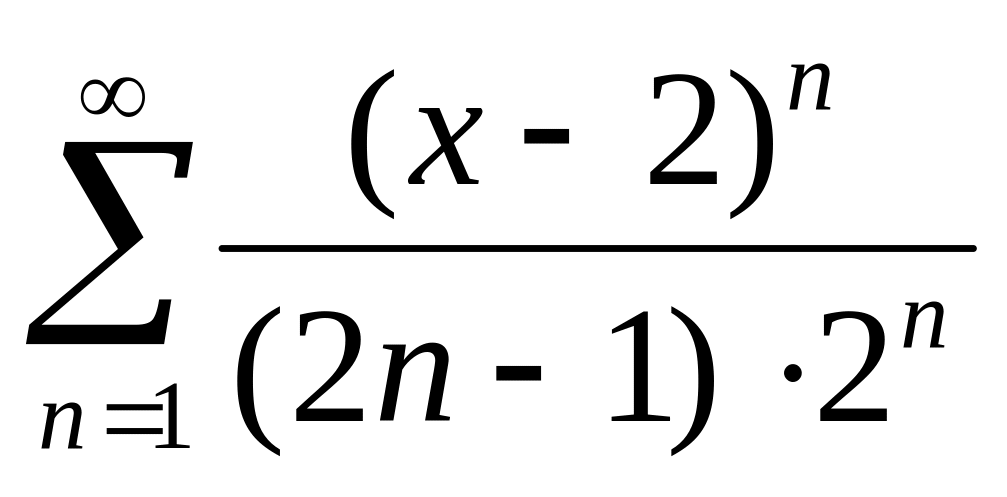
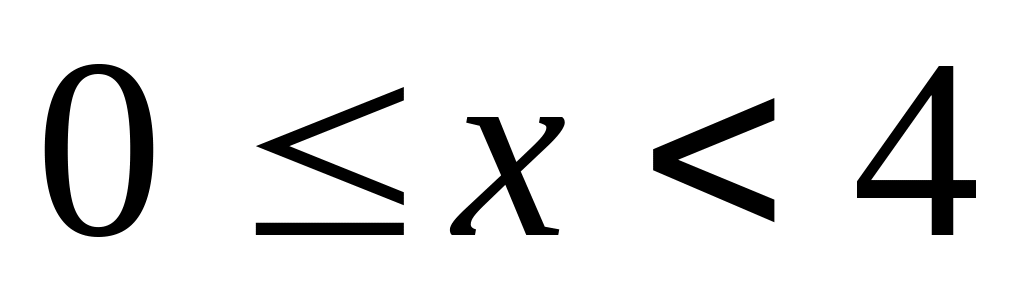
11
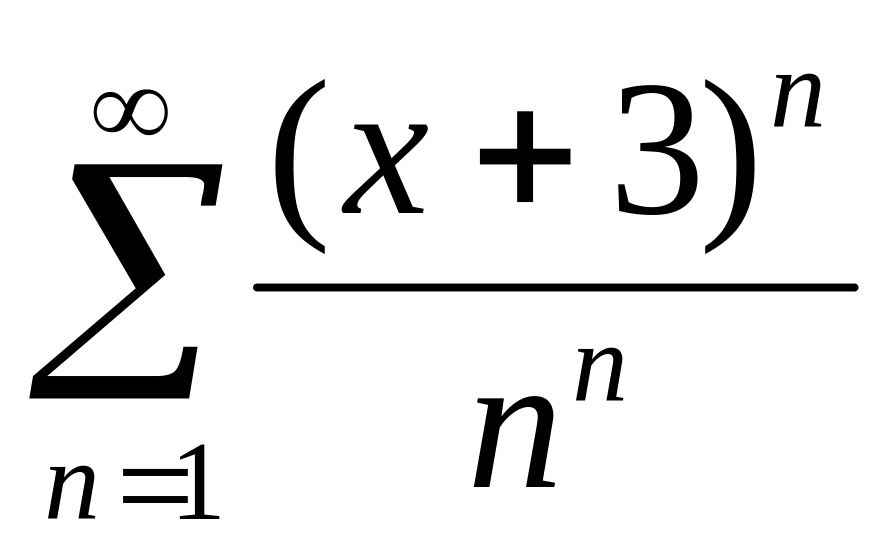
12
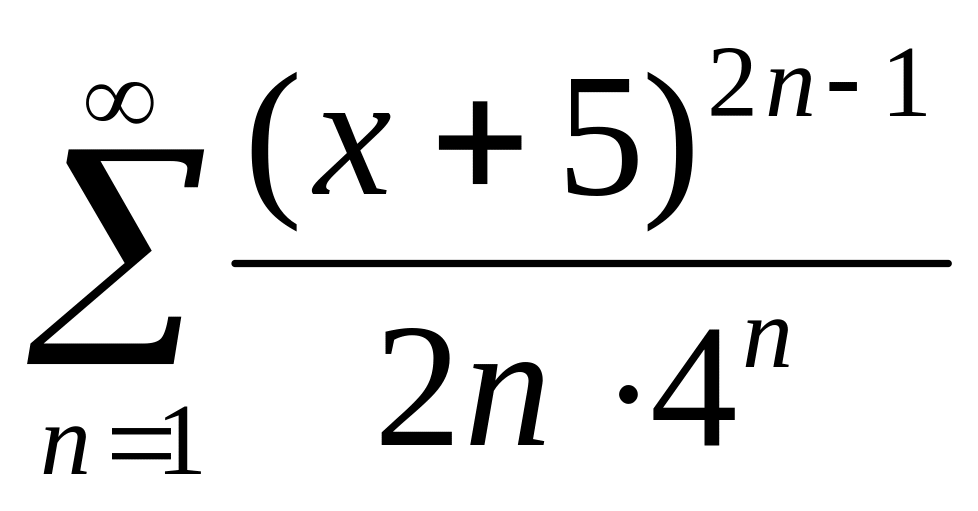
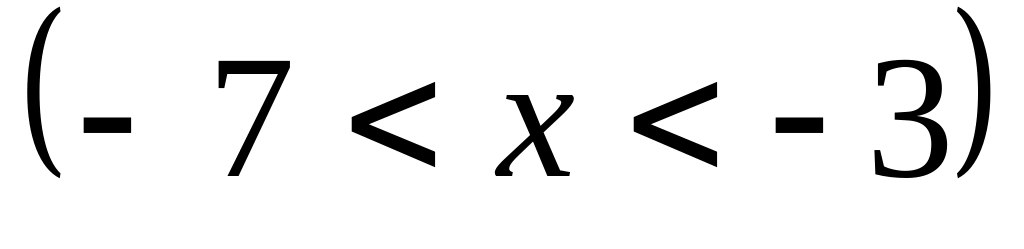
13
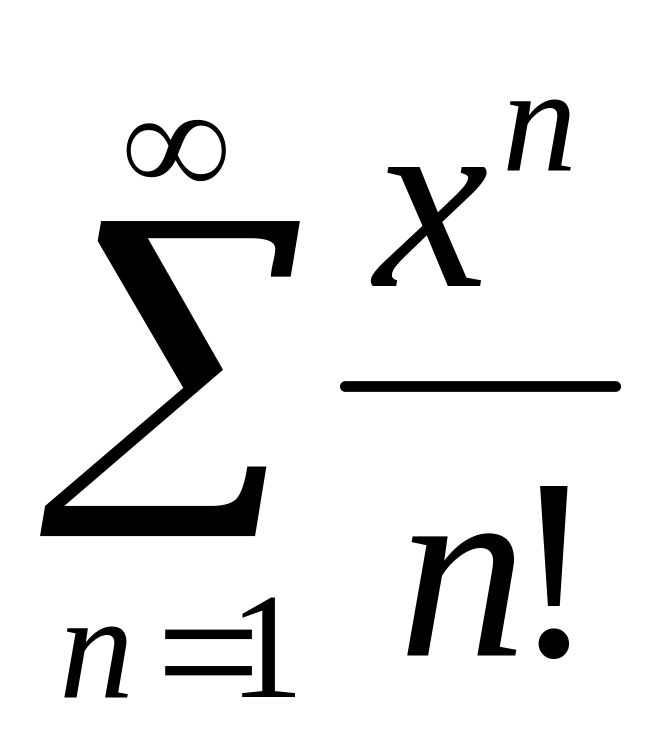
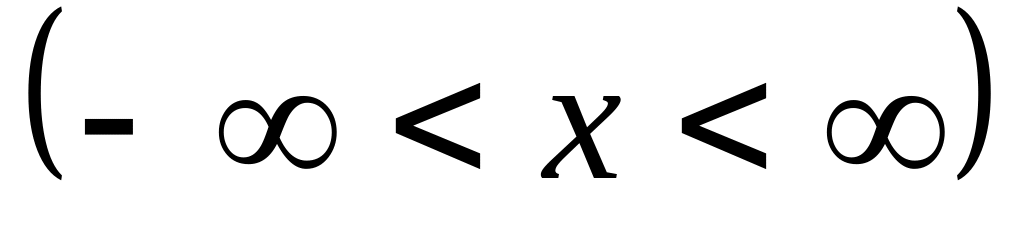
14
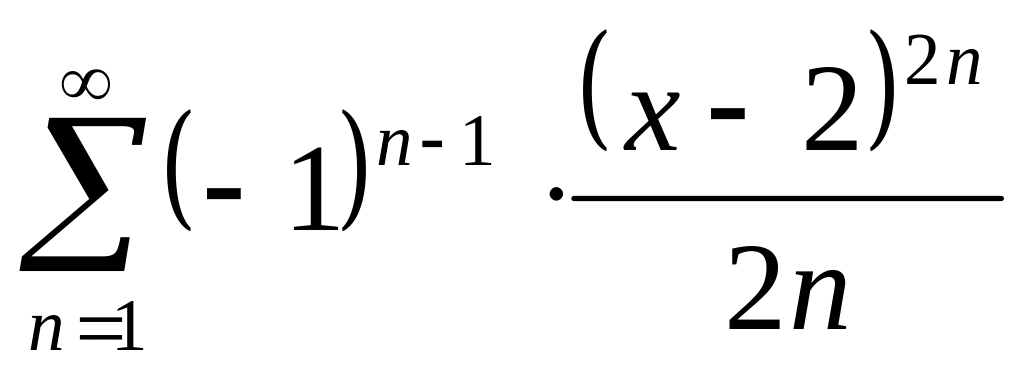
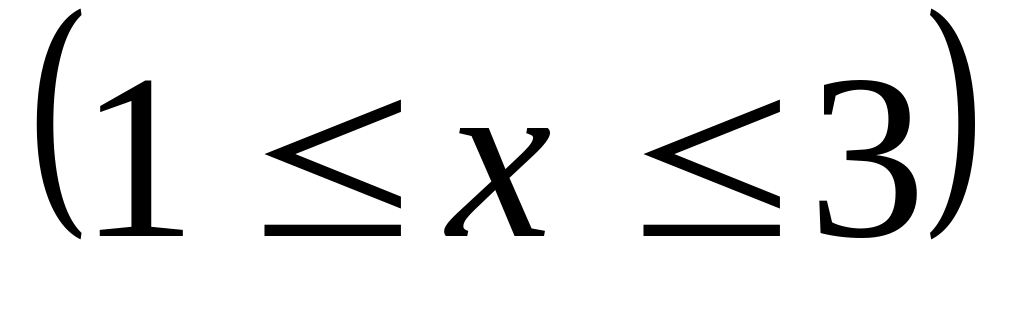
15
16
17
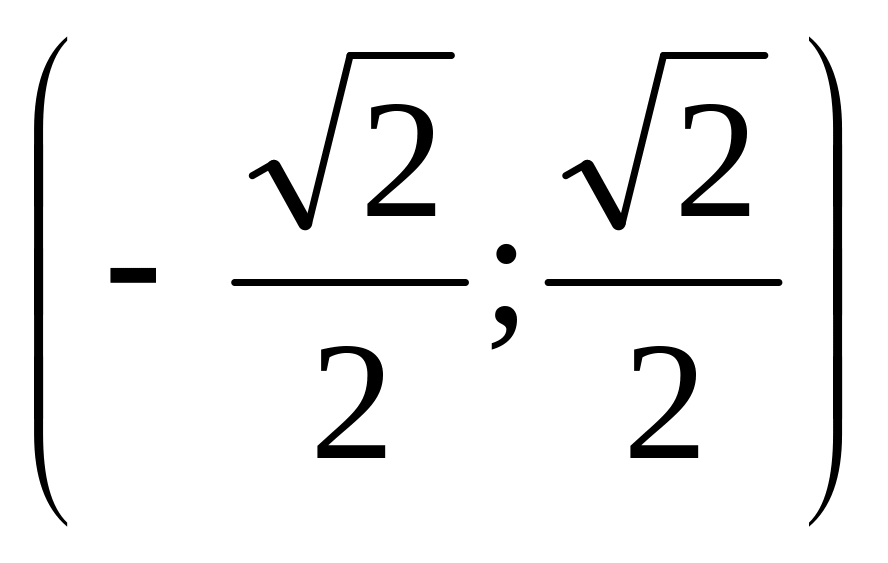
18
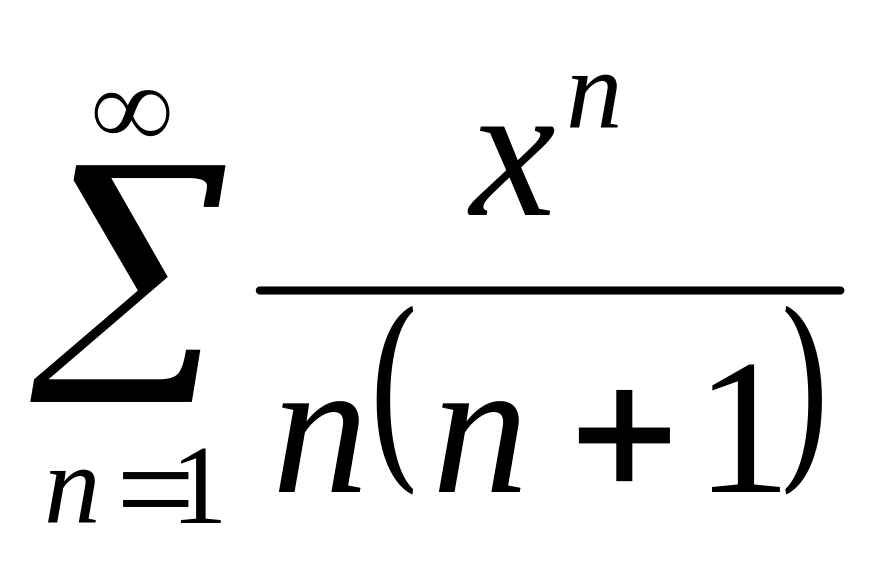
19
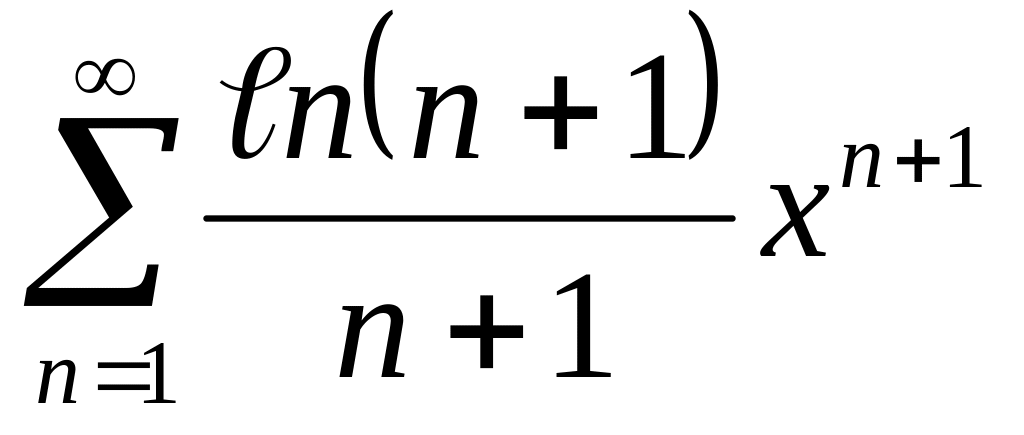
20
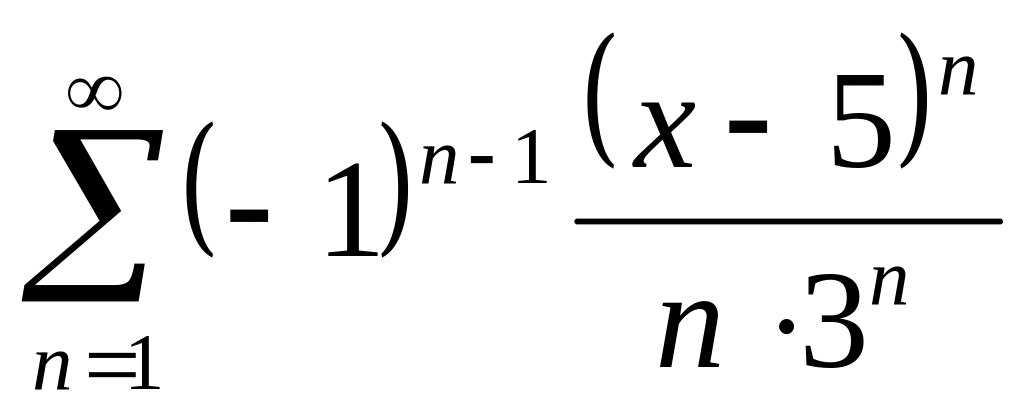
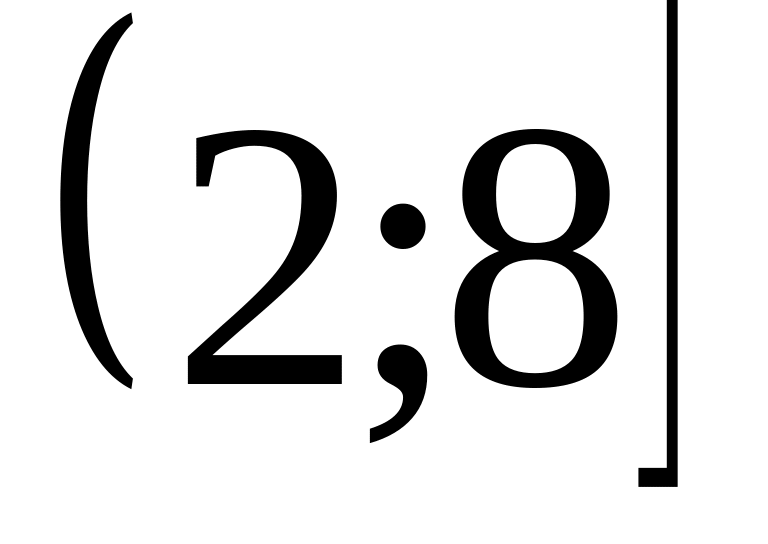
21
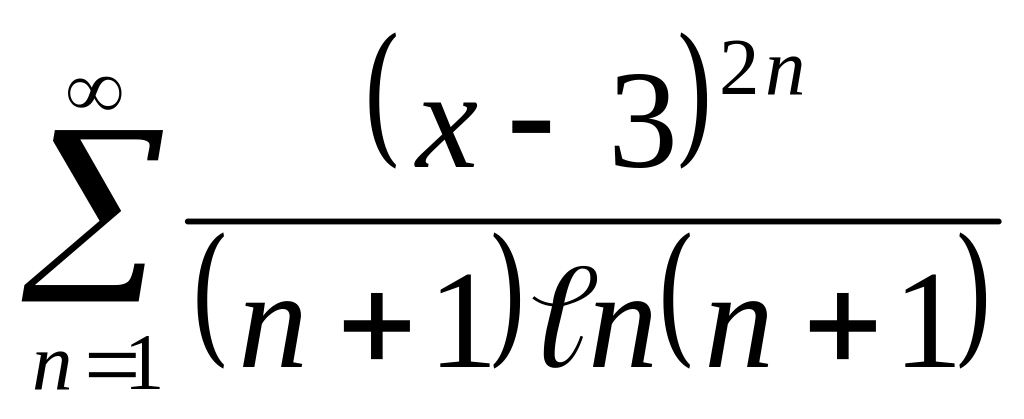
22
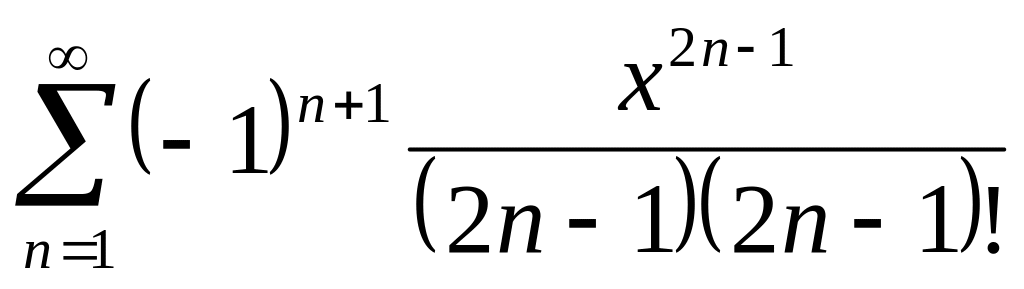
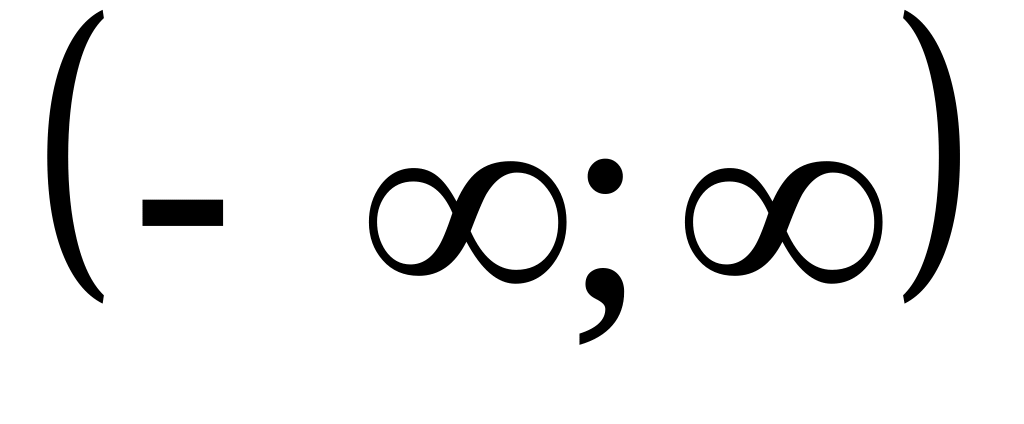
23
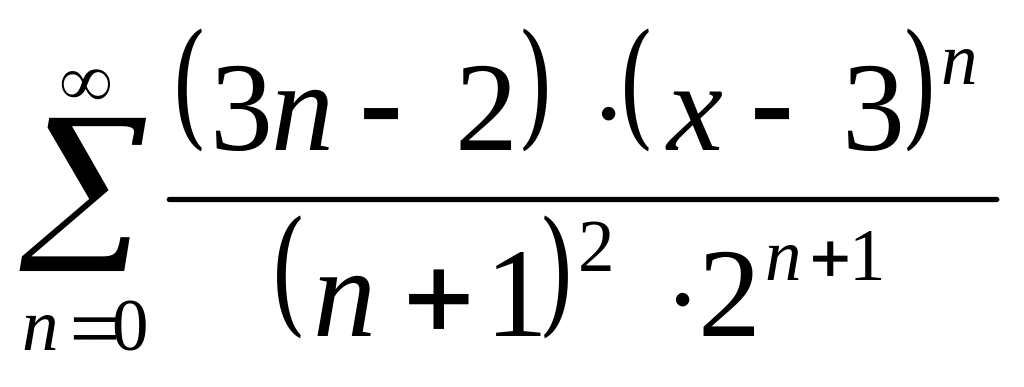
24
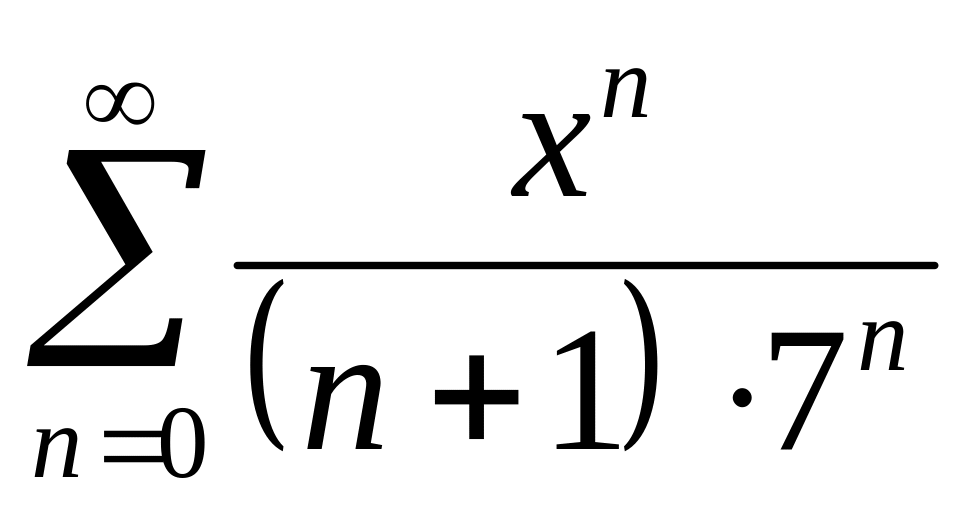
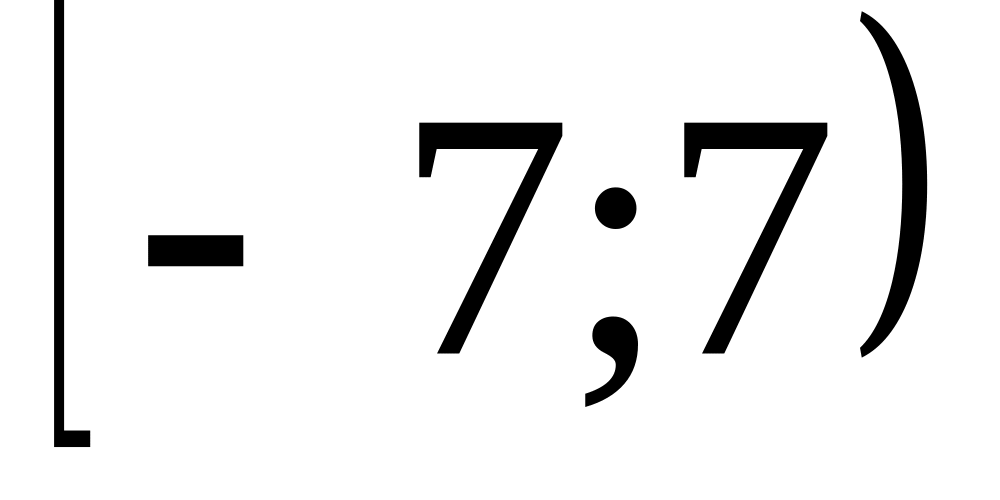
25
3. Вычислить определенный интеграл с точностью до путем предварительного разложения подинтегральной функции в ряд и почленного интегрирования. (13 неделя)
1)
;
;
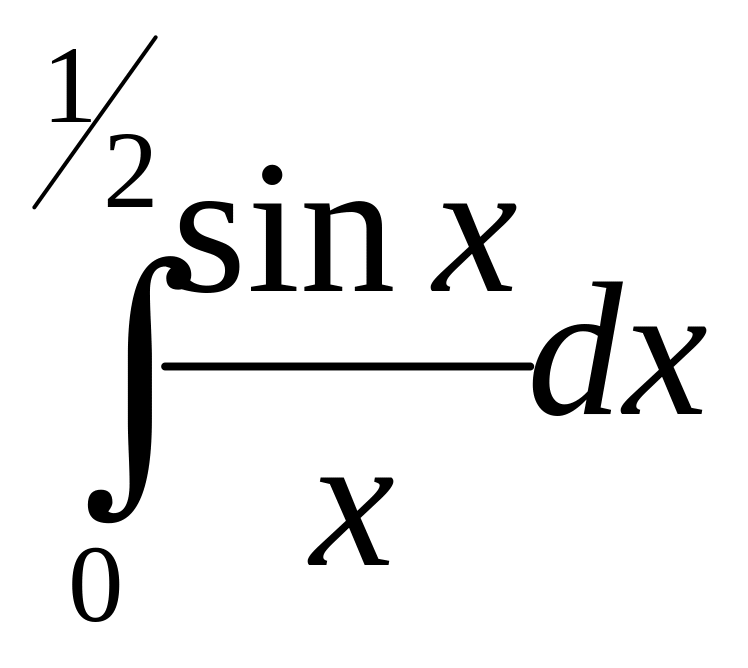ответ
2)
ответ 0,7468
3)
ответ 0,608
4)
ответ 0,621
5)
ответ 0,2505
6)
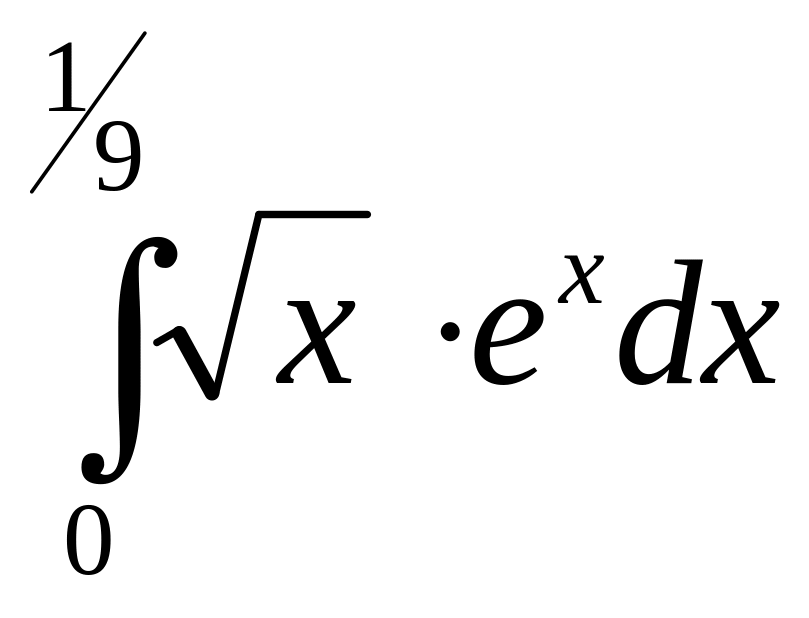ответ 0,026
7)
ответ 32,831
8)
ответ 0,487
9)
ответ 0,006
10)
ответ 0,494
11)
ответ 0,6449
12)
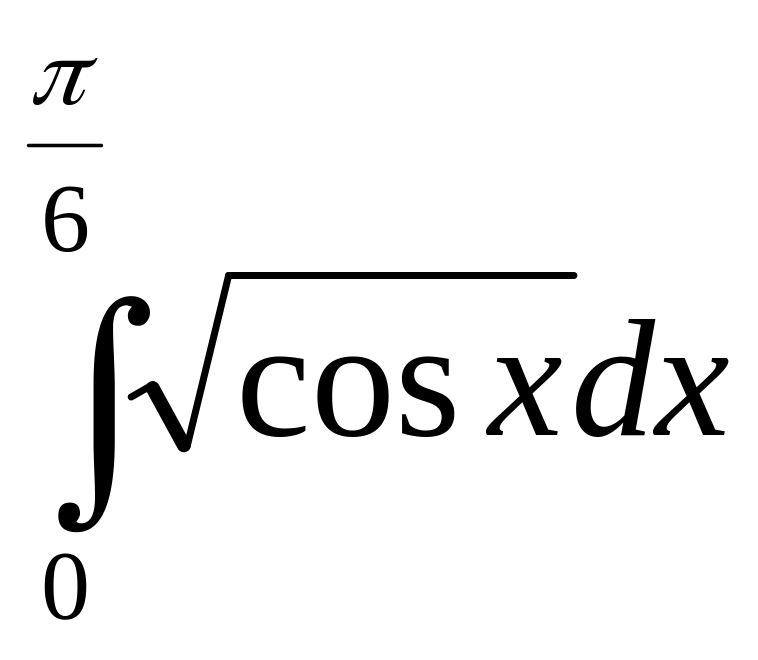ответ 0,511
13)
ответ 0,2800
14)
ответ 0,1991
15)
ответ 0,4802
16)
ответ 0,7714
17)
ответ 0,9461
18)
ответ 0,337
19)
ответ 2,835
20)
ответ 8,041
21)
ответ 0,119
22)
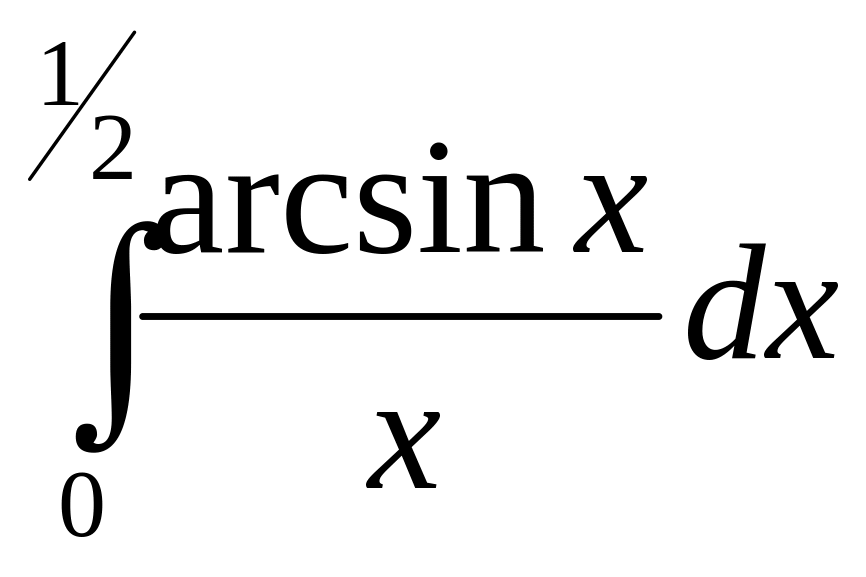ответ 0,507
23)
ответ 0,905
24)
ответ 0,927
25)
ответ 0,783