
- •Материалы для самостоятельной работы
- •Индивидуальное задание №1.
- •4. Дифференциальные уравнения высших порядков (3 неделя )
- •5. Найти общее решение неоднородного дифференциального уравнения (4 неделя )
- •6. Неоднородные дифференциальные уравнения с постоянными коэффициентами. Найти решение задачи Коши. (4 неделя )
- •7. Неоднородные дифференциальные уравнения с постоянными коэффициентами. Найти решение задачи Коши (4 неделя )
- •Индивидуальное задание№2.
- •1. Вычислить двойной интеграл (5 неделя)
- •2. Изменить порядок интегрирования (5 неделя)
- •3. Вычислить площадь фигур, ограниченных заданными линиями (6 неделя)
- •4. Нарисовать тела, ограниченные данными поверхностями.
- •5. Вычислить тройной интеграл (7 неделя)
- •6. Найти объемы тел, ограниченных данными поверхностями (7 неделя)
- •Индивидуальное задание№3.
- •1. Криволинейный интеграл первого рода и его приложения. (9 неделя)
- •2. Криволинейный интеграл второго рода и его приложение. (9 неделя)
- •3. Интеграл по поверхности 1 рода. (10 неделя)
- •4. Интегралы по поверхности II рода. (10 неделя)
- •Ответ: 0
- •5. Используя теорему Остроградского - Гаусса решить задачи (10 неделя)
- •10. Найти поток вектора через границу части шара заключенной в I-ом октанте. Ответ:
- •Индивидуальное задание№4.
- •На признак Даламбера, Коши. (11 неделя)
- •Б) Применить признак Лейбница (12 неделя)
- •Найти интервалы сходимости (радиус сходимости) и определить тип сходимости на концах интервала сходимости данных рядов. (13 неделя)
- •3. Вычислить определенный интеграл с точностью до путем предварительного разложения подинтегральной функции в ряд и почленного интегрирования. (13 неделя)
- •Индивидуальное задание №5.
5. Вычислить тройной интеграл (7 неделя)
1.
![]() ,
,
![]() Ответ:
10
Ответ:
10
2.
 ,
,
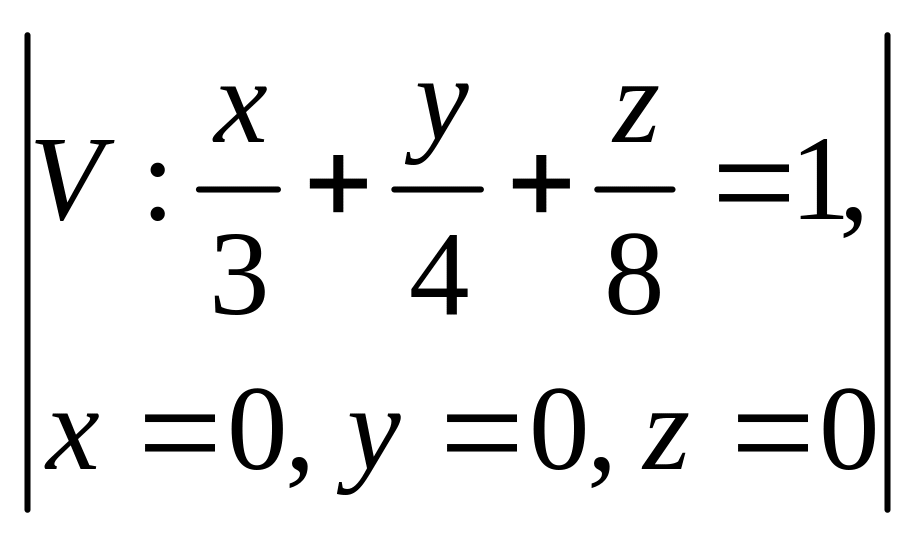 Ответ:
0
Ответ:
0
3.
![]() ,
,
![]() Ответ: 1
Ответ: 1
4.
![]() ,
,
![]() Ответ: 7
Ответ: 7
5.
![]() ,
,
![]() Ответ: 12
Ответ: 12
6.
![]() ,
,![]() Ответ:
8
Ответ:
8
7.
![]() ,
,
![]() Ответ:
225
Ответ:
225
8.
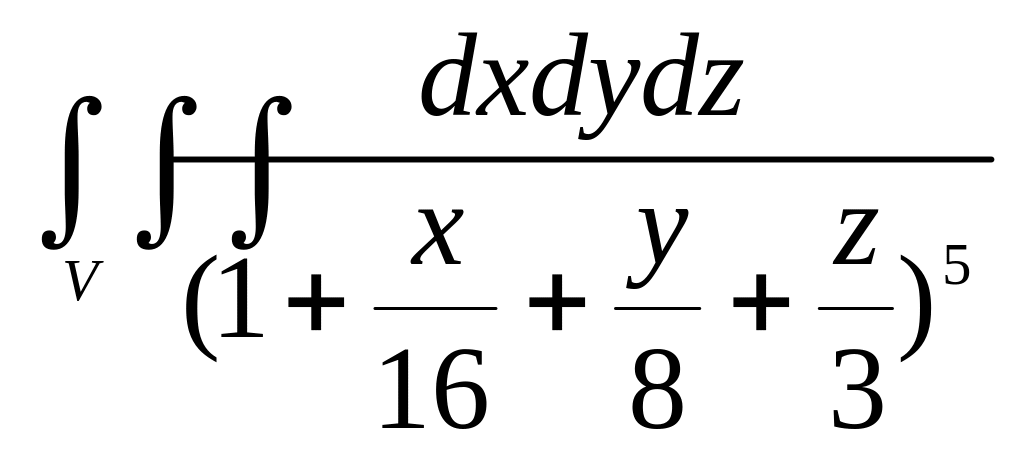 ,
,  Ответ:
5
Ответ:
5
9.
![]() ,
,
![]() Ответ: 18
Ответ: 18
10. , Ответ: 18
11. , Ответ: 1
12.
![]() ,
,
![]() Ответ: 96
Ответ: 96
13.
![]() ,
,
![]() Ответ: 64
Ответ: 64
14.
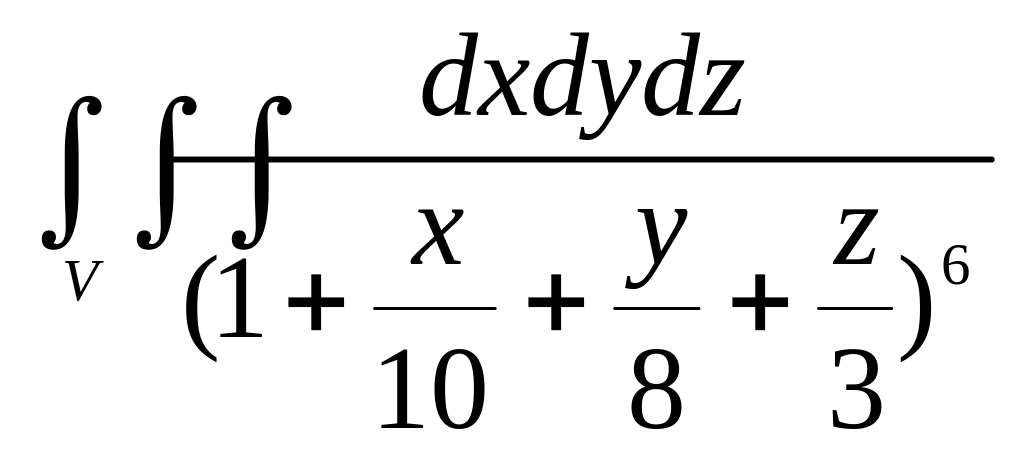 ,
,
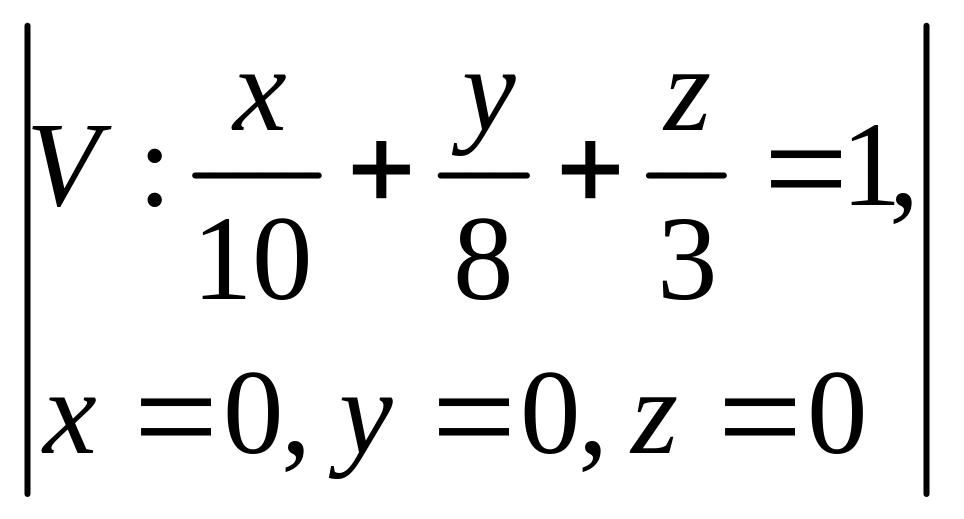 Ответ: 2
Ответ: 2
15.
![]() ,
, ![]() Ответ: 2
Ответ: 2
16.
![]() ,
,
![]() Ответ:
23
Ответ:
23
17.
![]() ,
,
![]() Ответ: 25
Ответ: 25
18.
![]() ,
, ![]() Ответ: 34
Ответ: 34
19. , Ответ: 2
20.
![]() ,
, ![]() Ответ: 1
Ответ: 1
6. Найти объемы тел, ограниченных данными поверхностями (7 неделя)
1. Плоскостями координат, плоскостями
х=4, у=4 и параболоидом вращения
![]() Ответ:
Ответ:
![]() .
.
2. Поверхностями
![]() .
.
Ответ:
![]() .
.
3. Поверхностями
![]() .
.
Ответ:
![]() .
.
4. Поверхностями
![]() .
.
Ответ:
![]() .
.
5. Поверхностями
![]() .
.
Ответ: .
6. Поверхностями
![]()
Ответ:
![]() .
.
7. Поверхностями
![]()
Ответ:
![]()
8. Поверхностями
![]()
Ответ:
![]()
9. Поверхностями
![]() и расположенного в первой октанте.
и расположенного в первой октанте.
Ответ: 12.
10. Поверхностями ![]()
Ответ:
![]()
11. Поверхностями ![]()
Ответ:
![]()
12. Координатными плоскостями,
плоскостью
![]() и цилиндром
и цилиндром
![]()
Ответ: 16.
13. Поверхностями
![]()
Ответ:
![]()
14. Поверхностями ![]()
Ответ: 6.
15. Поверхностями ![]()
Ответ:
![]()
16. Поверхностями ![]()
Ответ:
17. Плоскостями
![]()
Ответ: 12.
18. Координатными плоскостями,
плоскостью
и цилиндром
![]()
Ответ: 16.
19. Цилиндром
![]() ,
координатными плоскостями и плоскостью
,
координатными плоскостями и плоскостью
![]()
![]() . Ответ:
45.
. Ответ:
45.
20. Цилиндром
![]() ,
координатными плоскостями и плоскостью
,
координатными плоскостями и плоскостью
![]()
![]() . Ответ:
. Ответ:
![]()
Литература: 1,2,4,10,14,16,22,23 26,27.
Индивидуальное задание№3.
Тема: «Криволинейный интеграл и интегралы по поверхности».
Цель- усвоить основные свойства криволинейных интегралов и интегралов по поверхности.
Задание:
1. Криволинейный интеграл первого рода и его приложения. (9 неделя)
Найти массу всей кардиоиды
 , если
, если
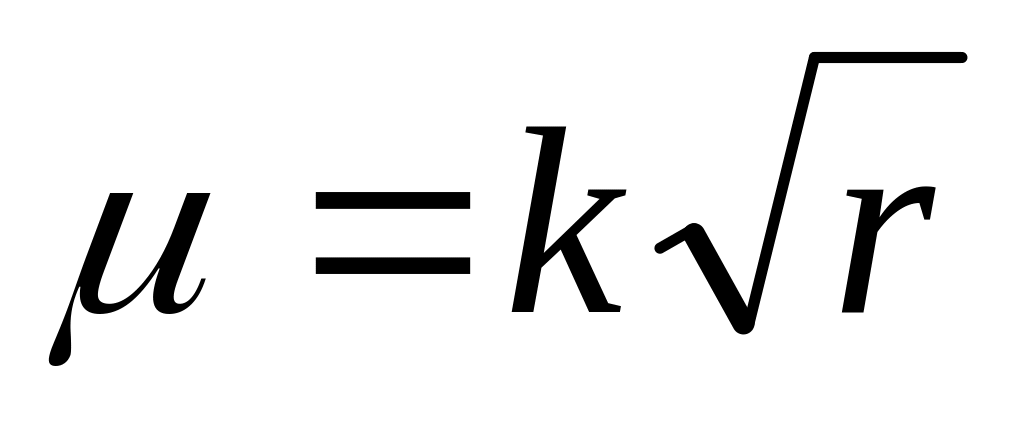 . Ответ:
. Ответ:
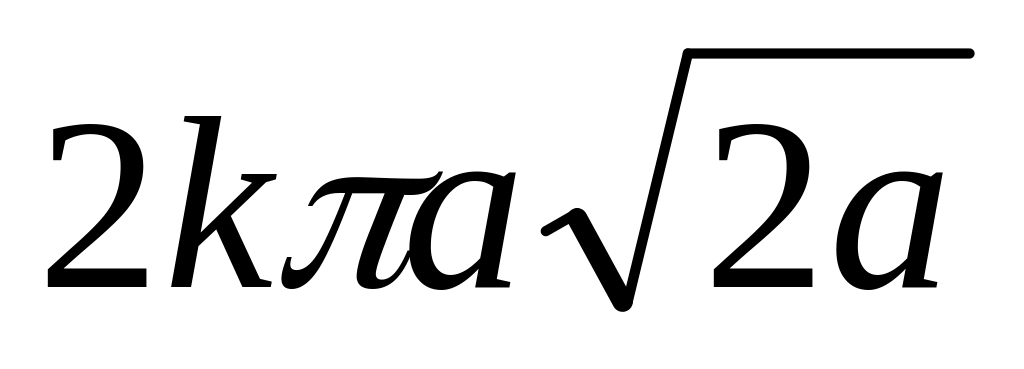
Найти массу всей лемнискаты
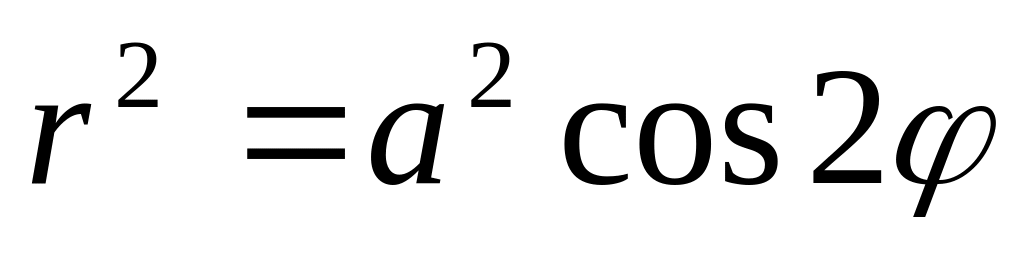 ,
если
,
если
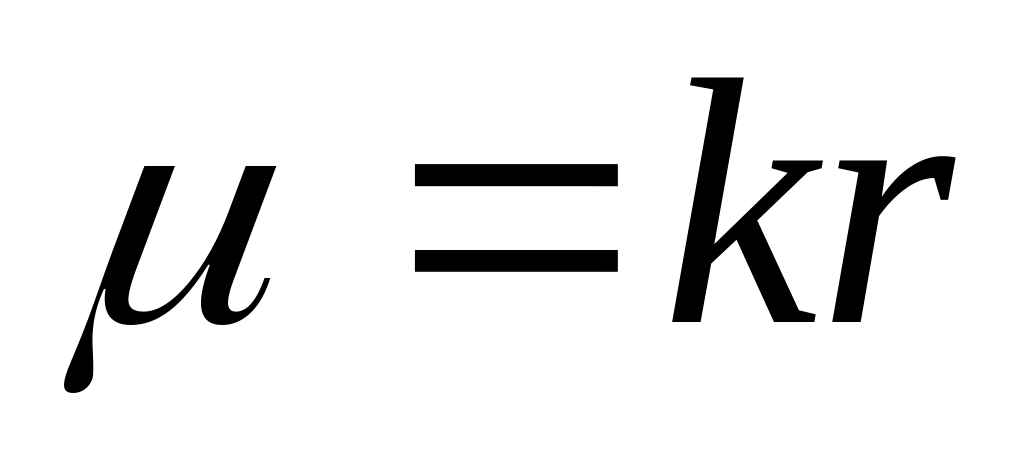 . Ответ:
. Ответ: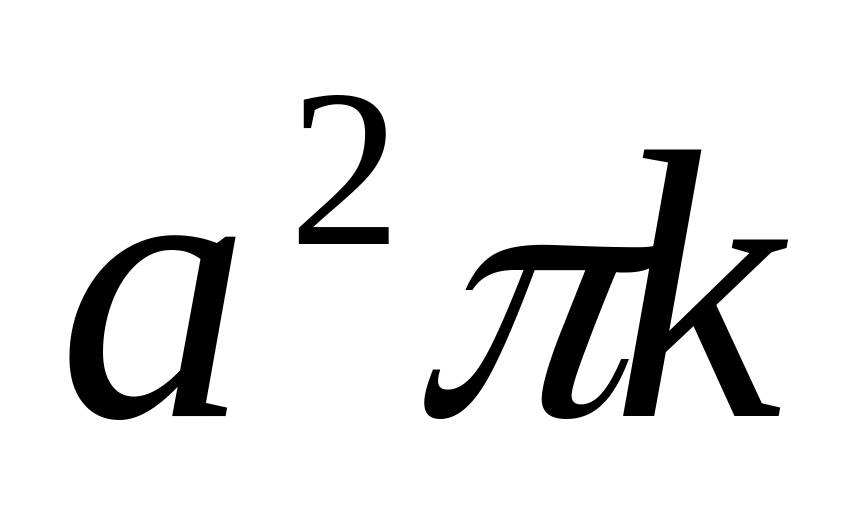
Вычислить
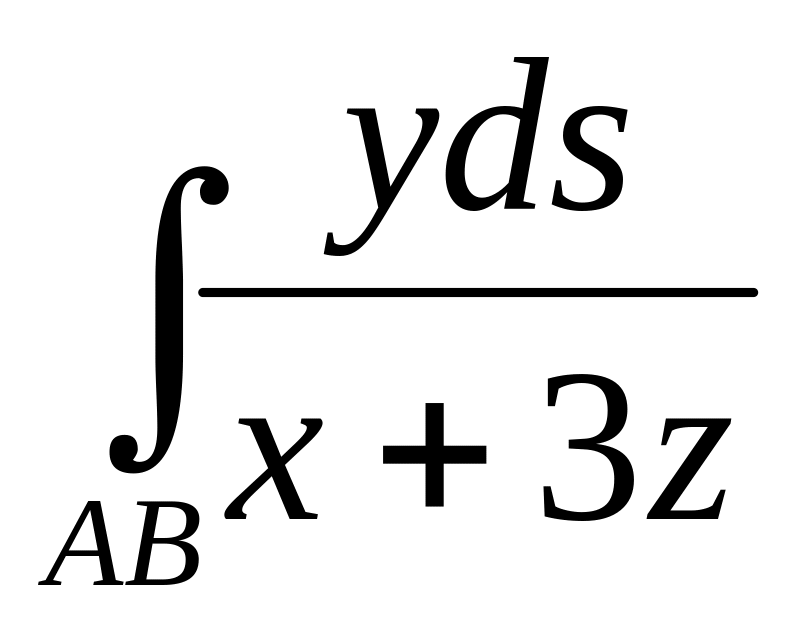 ,
если АВ- дуга линии
,
если АВ- дуга линии
 Ответ:
Ответ:
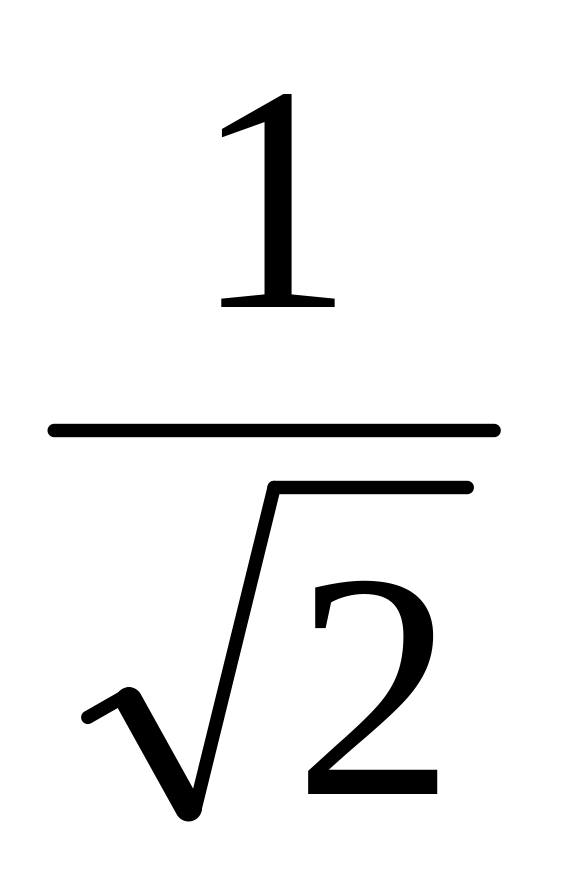
Найти массу дуги конической винтовой линии
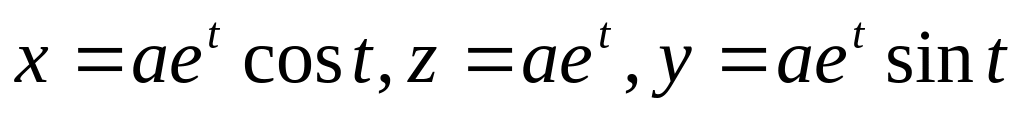 ,
если плотность вещества
,
если плотность вещества
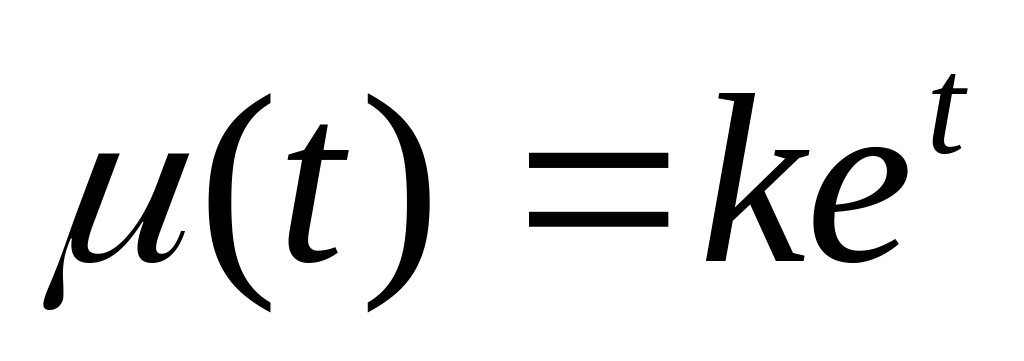 ,
от точки О(0,0,0,) до точки А(
,
от точки О(0,0,0,) до точки А( ). Ответ:
). Ответ:
Найти массу четверти окружности
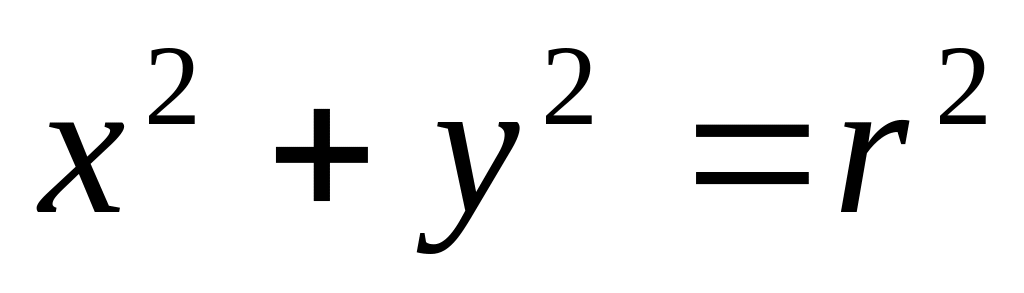 расположенной в первом квадранте, если
плотность ее
расположенной в первом квадранте, если
плотность ее
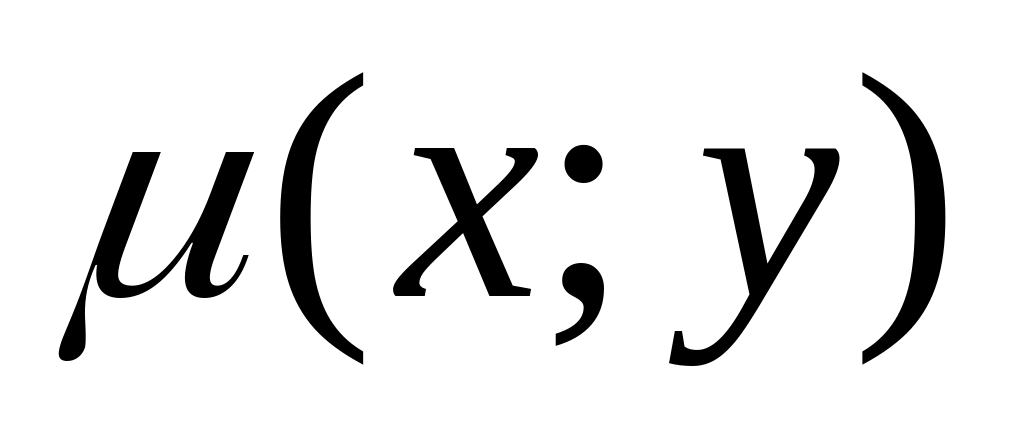 в каждой точке пропорциональна абсциссе
этой точки (коэффициент пропорциональности
в каждой точке пропорциональна абсциссе
этой точки (коэффициент пропорциональности
 ). Ответ:
β r2
). Ответ:
β r2Вычислить
 ,
где
,
где
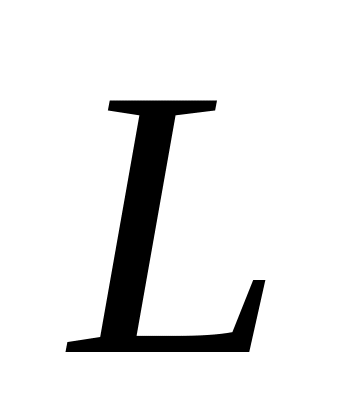 -контур
прямоугольника с вершинами в точках
А(0;0), В(4;0), С(4;2) и D(0;2). Ответ:
24
-контур
прямоугольника с вершинами в точках
А(0;0), В(4;0), С(4;2) и D(0;2). Ответ:
24Вычислить
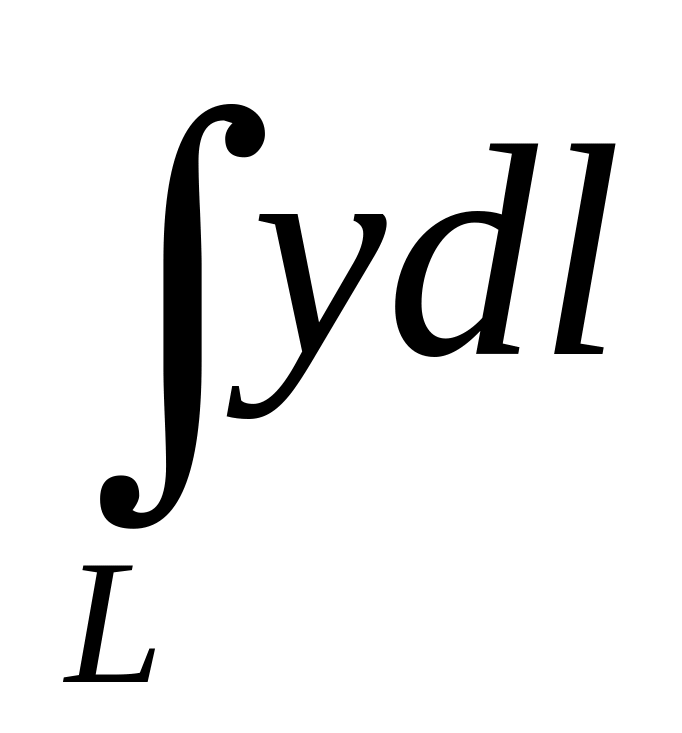 ,
где
-
дуга параболы
,
где
-
дуга параболы
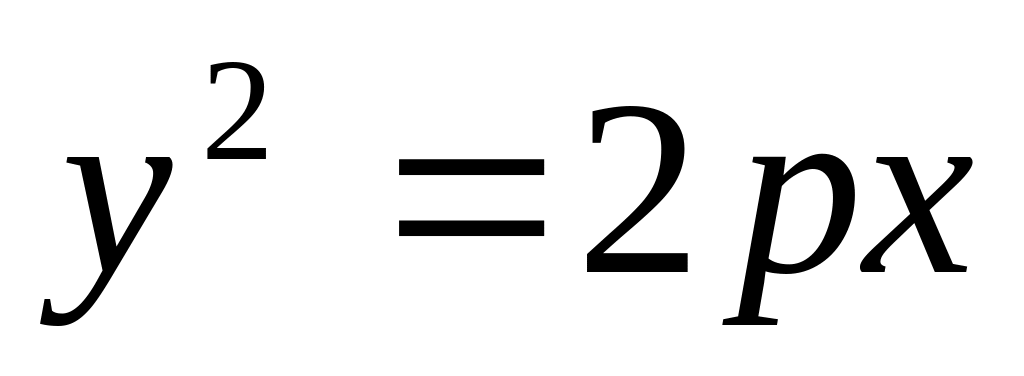 отсеченная параболой
отсеченная параболой
 .
.
Ответ:
![]()
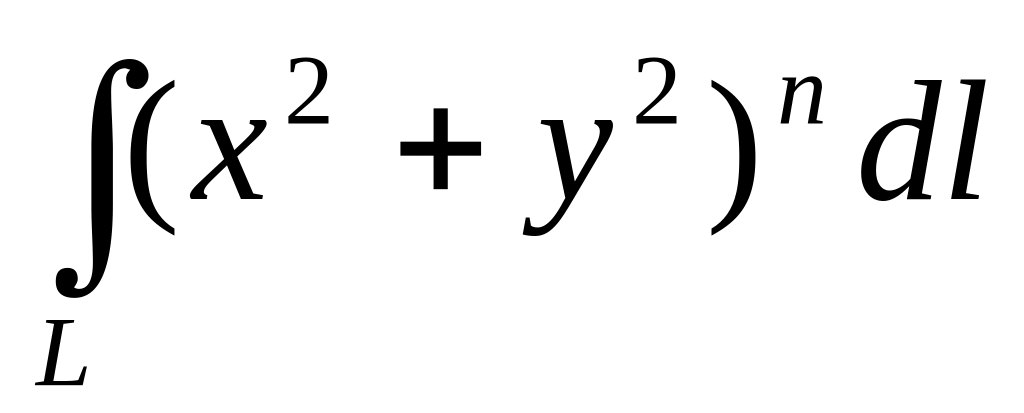 ,
где
-
окружность
,
где
-
окружность
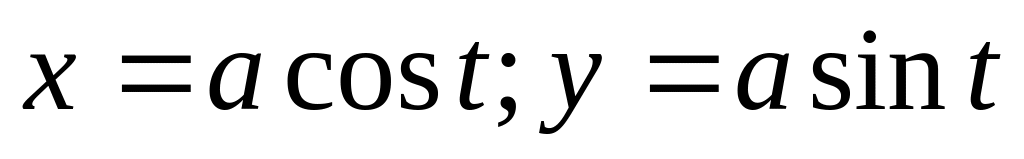 . Ответ:
. Ответ:
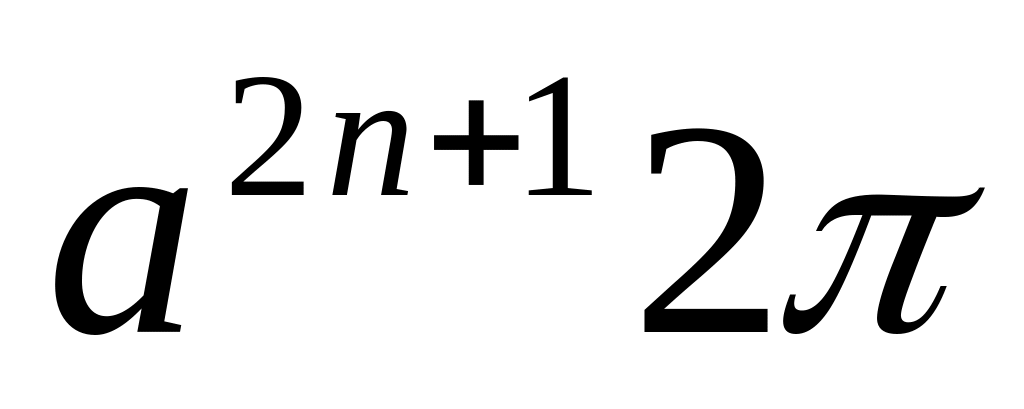
Вычислить , где -четверть эллипса
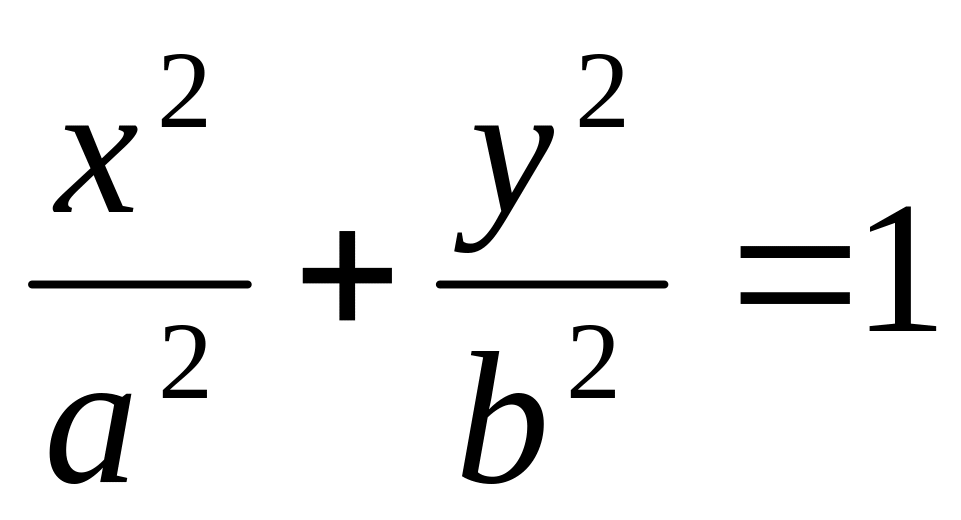 лежащая в первом квадранте.
лежащая в первом квадранте.
Ответ:
![]()
Вычислить
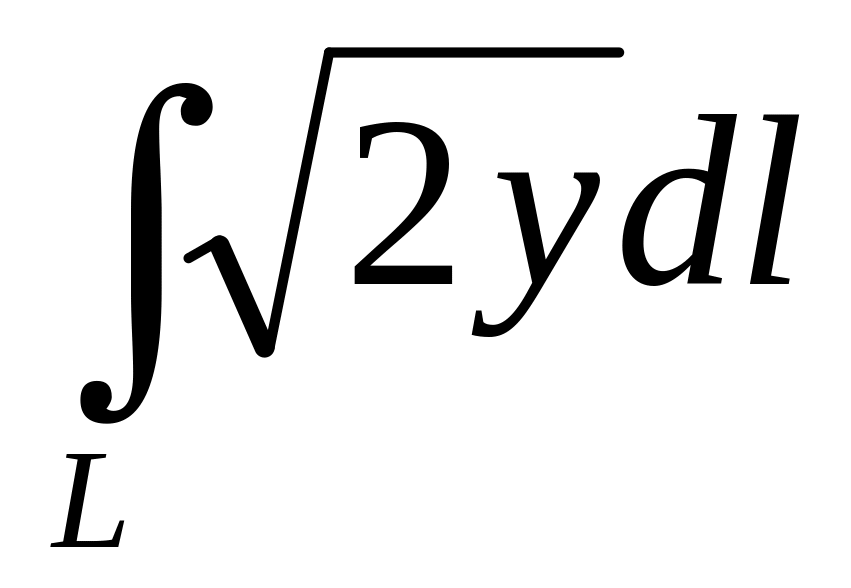 ,
где
-первая
арка циклоиды
,
где
-первая
арка циклоиды
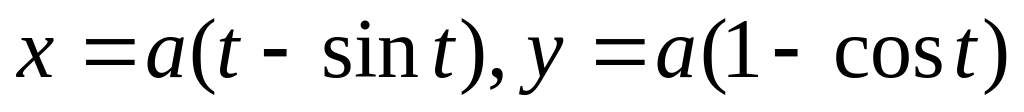 .
.
Ответ:
![]()
Вычислить
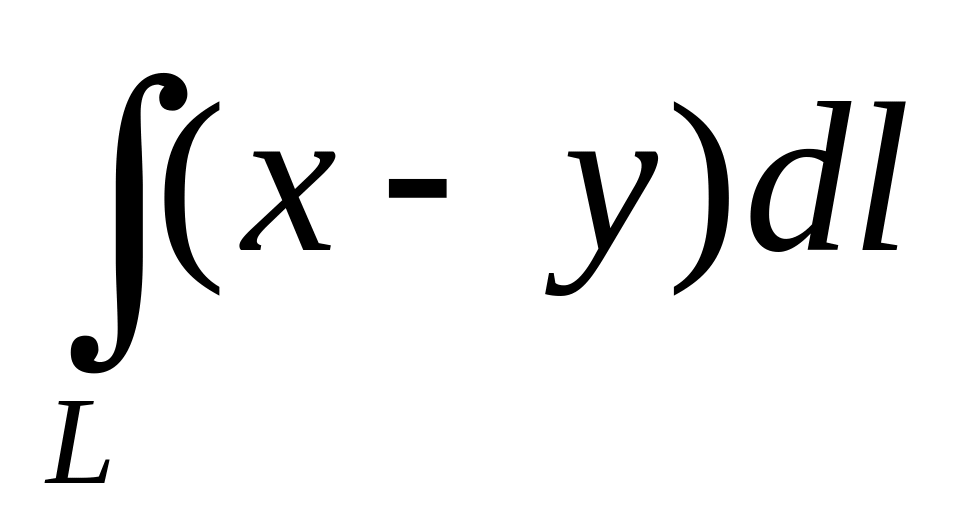 ,
где
-
окружность
,
где
-
окружность
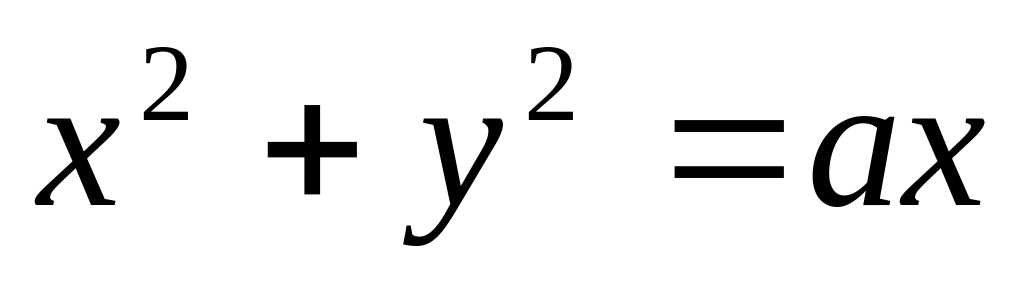 . Ответ:
. Ответ:

Вычислить
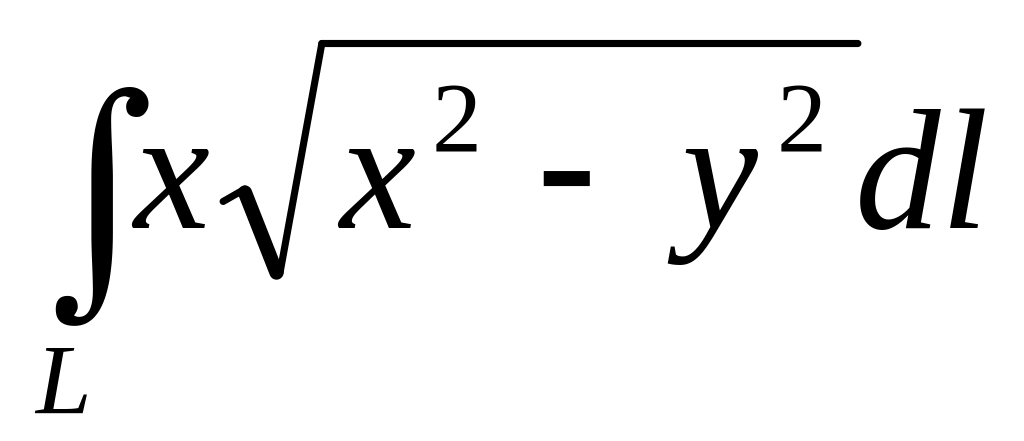 ,
где
-
половина лемнискаты
,
где
-
половина лемнискаты
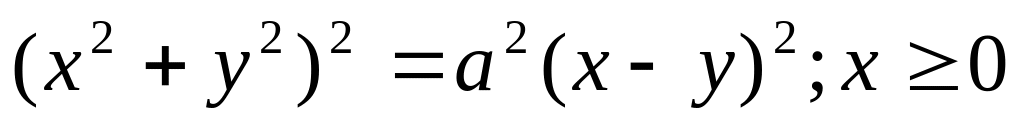
Ответ:
![]()
Вычислить
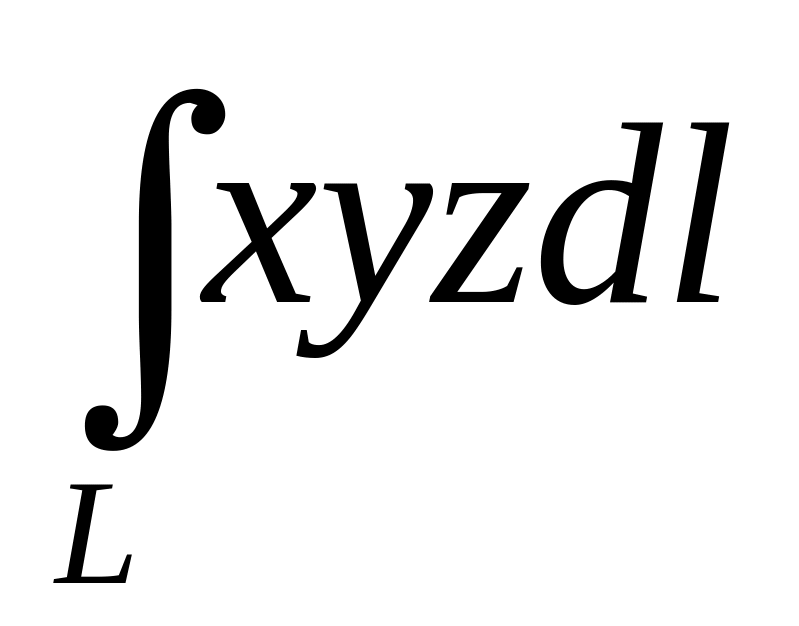 ,
где
-
четверть окружности
,
где
-
четверть окружности
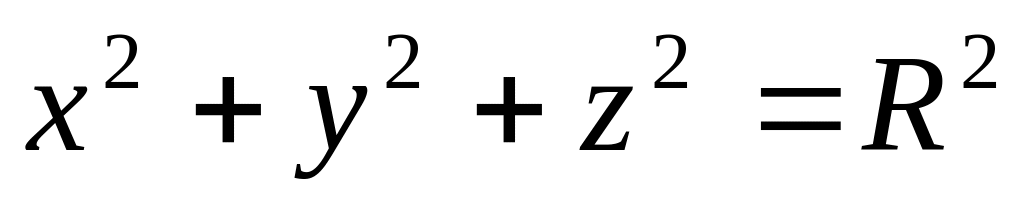 и
и
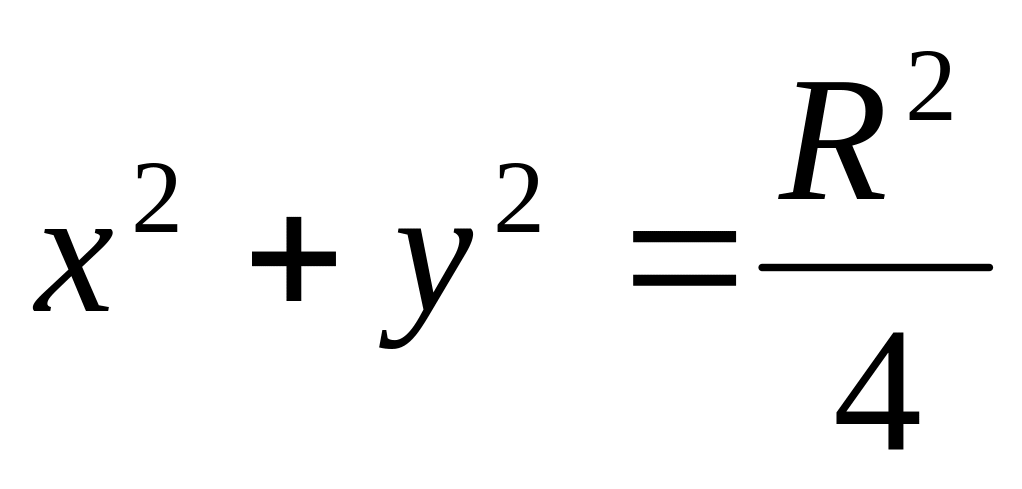 лежащая в первом октанте. Ответ:
лежащая в первом октанте. Ответ:
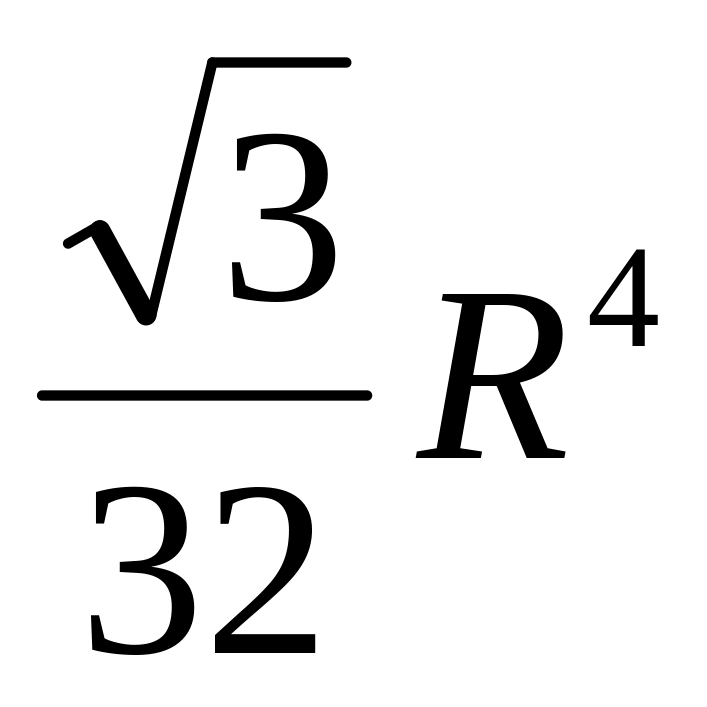
Вычислить
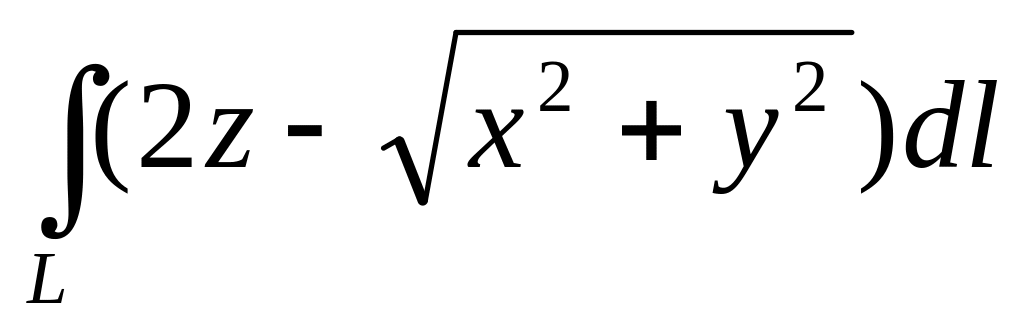 ,
где
-первый
виток винтовой линии
,
где
-первый
виток винтовой линии
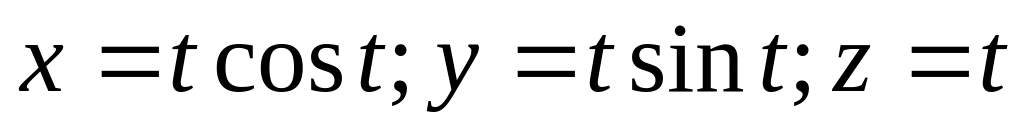 . Ответ:
. Ответ:

Вычислить , где - четверть окружности ,
 лежащая в первом октанте. Ответ:
лежащая в первом октанте. Ответ:
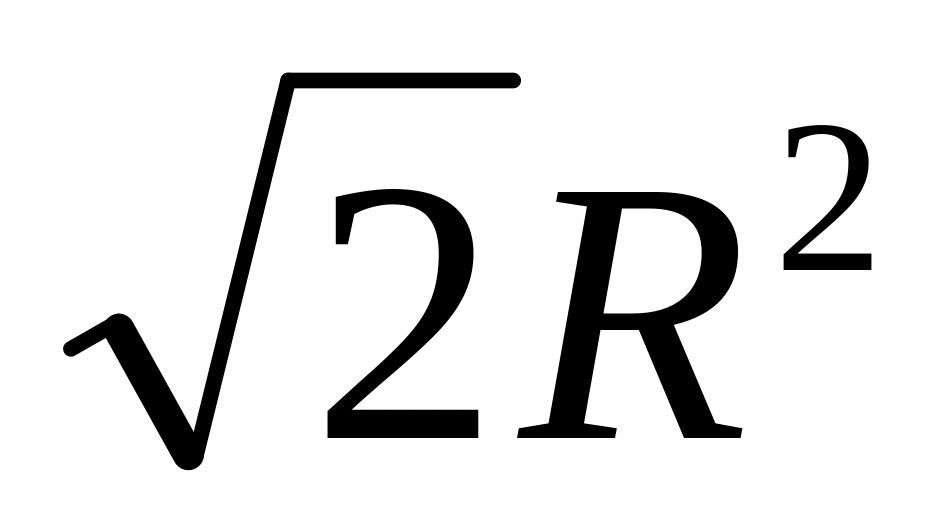
Найти массу участка линии
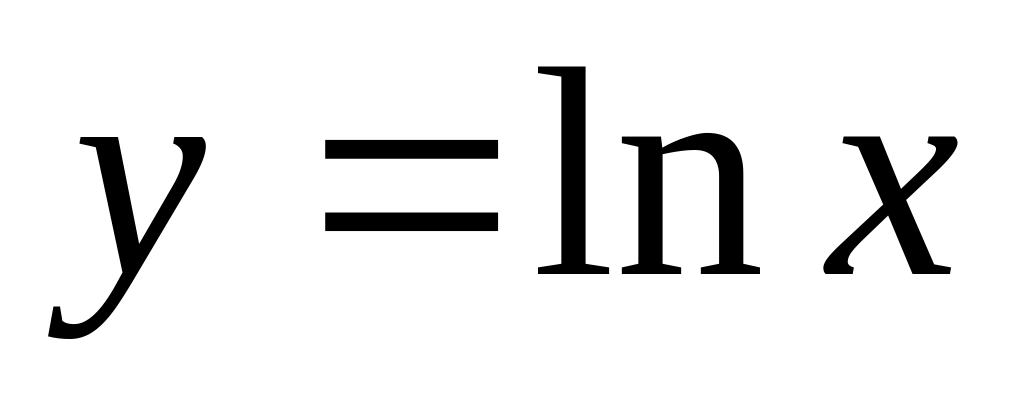 между точками с абсциссами
между точками с абсциссами
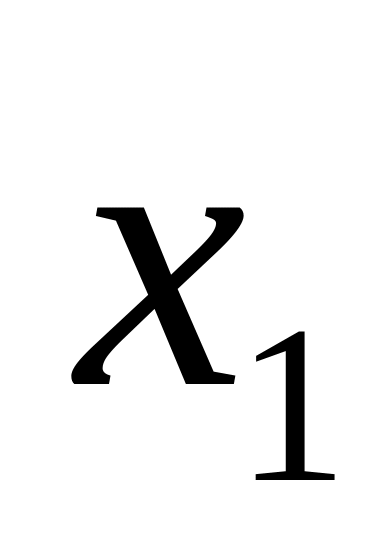 и
и
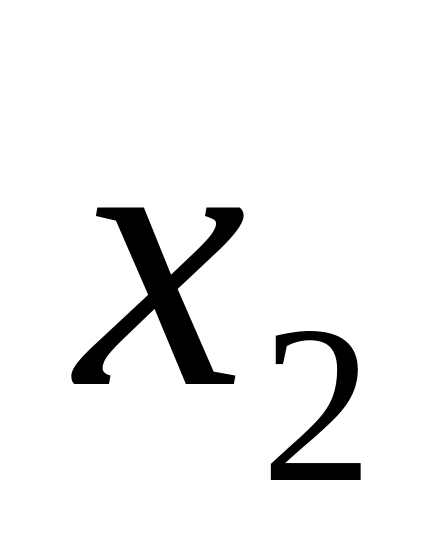 ,
если плотность линии в каждой точке
равна квадрату абсциссы
точки. Ответ:
,
если плотность линии в каждой точке
равна квадрату абсциссы
точки. Ответ:
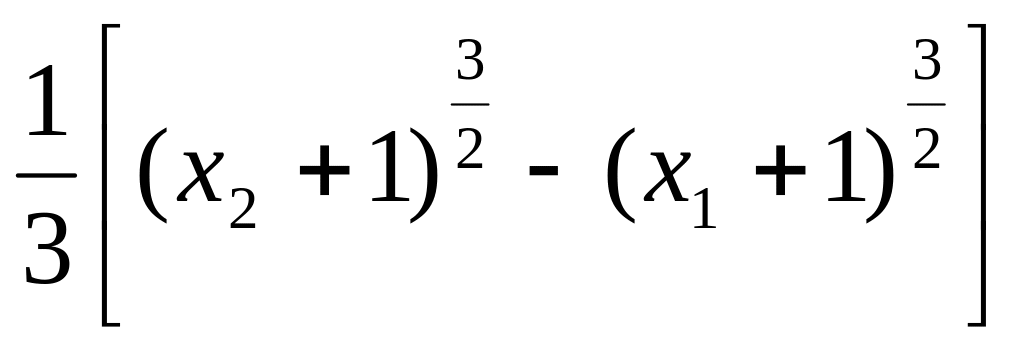
Найти массу первого витка винтовой линии
 плотность которой в каждой точке равна
квадрату полярного радиуса этой точки.
плотность которой в каждой точке равна
квадрату полярного радиуса этой точки.
Ответ:
![]()
Найти координаты первого полувитка винтовой линии считая плотность постоянной. Ответ:
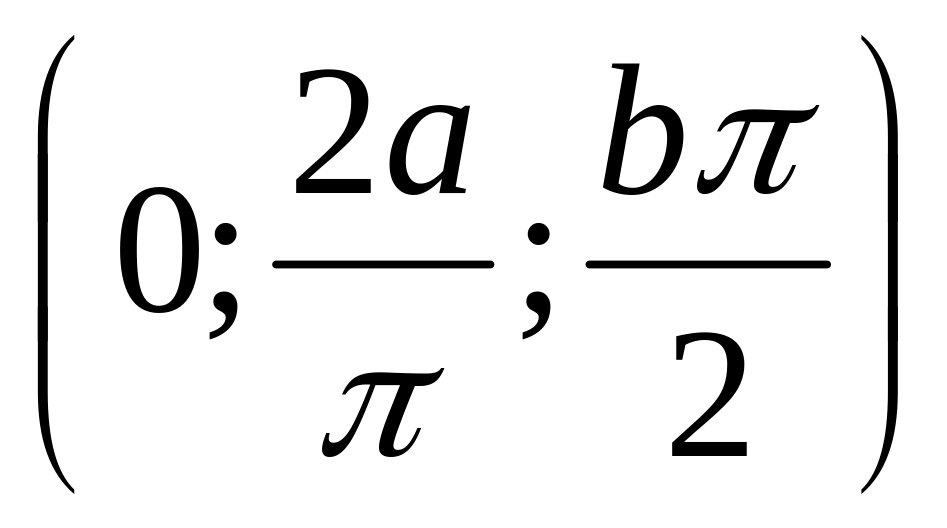
Вычислить статистический момент первого витка конической винтовой линии
 относительно плоскости ХОУ считая
плотность пропорциональной квадрату
расстояния от плоскости
относительно плоскости ХОУ считая
плотность пропорциональной квадрату
расстояния от плоскости
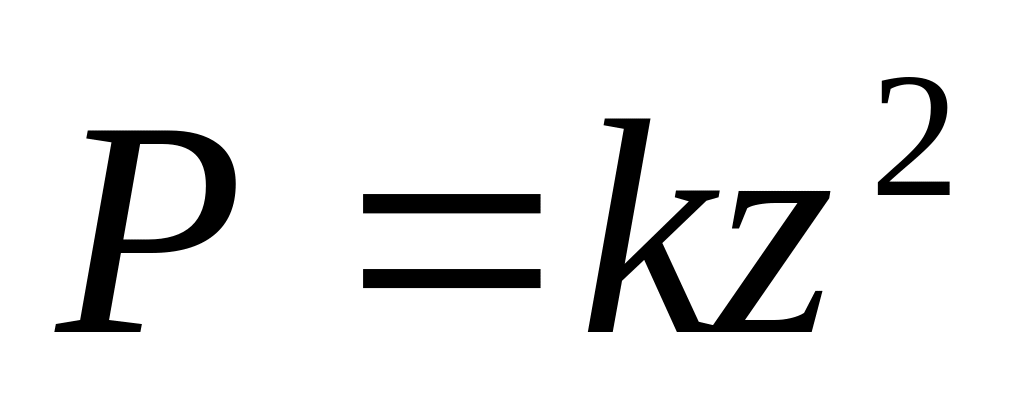 . Ответ:
. Ответ:
Вычислить моменты инерции относительно координатных осей первого витка винтовой линии
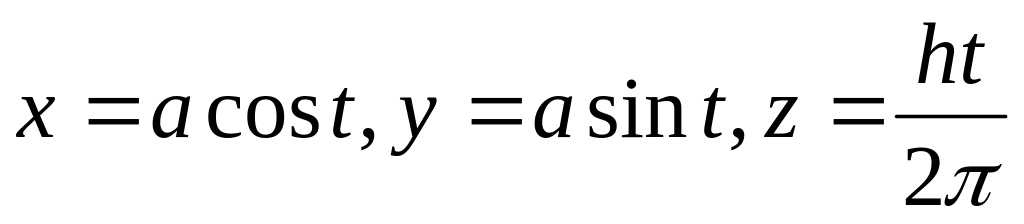 .
.
Ответ:![]()
