Лекции 4-6

© Михрин С.Б

§ 11 Векторный потенциал проводника с током

После того, как мы определили электрическое поле одного движущегося заряда, можем рассмотреть важный для решения практических задач случай упорядоченного движения многих зарядов в проводниках с токами.

Рассматривая движущиеся заряды, мы пришли к выводу, что электрическое поле, создаваемое ими, будет характеризоваться и скалярным и векторным потенциалами. Для электрического поля, созданного неподвижными зарядами векторный потенциал всюду равен нулю. А возможно ли существование такого электрического поля, для которого скалярный потенциал всюду равнялся бы нулю, а векторный нет?

Сначала рассмотрим кусок цилиндрического проводника, в котором за счет внешнего источника создается не исчезающее электрическое поле (рис.11.1).

Рис.11.1

Свободные носители заряда, концентрация которых в проводнике равна , в этом электрическом поле приходят в упорядоченное движение, которое характеризуется вектором скорости , ее иногда называют дрейфовой скоростью. Это определение используется потому, что скорость направленного движения много меньше средней скорости хаотического теплового движения свободных носителей заряда. Вектор параллелен вектору электрического поля в изотропном проводнике.

Определим ток в проводнике как заряд, пересекающий сечение проводника в единицу времени:

(11.1)

С другой стороны заряд , пересекающий сечение проводника за время равен: , где - заряд одного свободного носителя. В металлах свободные носители заряда – электроны. В жидких электролитах (растворах и расплавах солей) это могут быть многозарядные ионы, как положительно , так и отрицательно заряженные ; в плазме (ионизированный газ) это могут быть ионы и электроны. Из-за различия в массах ионов скорости направленного движения их в электрическом поле будут разными. Концентрации также будут в общем случае различаться, из-за различия зарядов ионов разного знака, при условии электрической нейтральности среды в целом. Для них . Вклад в общий заряд, проходящий через сечение проводника, потоки отрицательно и положительно заряженных ионов дают одного знака, поскольку вектора скоростей у разноименных ионов направлены в противоположные стороны. К вопросу об определении скорости направленного движения в электрическом поле мы вернемся позже.

Разделив силу тока в проводнике на площадь его поперечного сечения, получим плотность тока в однородном проводнике: .

Если проводник неоднородный, можно определить плотность тока в произвольной точке внутри проводника. Для этого сделаем сечение проводника произвольной поверхностью, на которой находится эта точка, выделим на ней элементарную площадку , на которую попадает эта точка. Заметим, что вектор - произвольное сечение трубки тока векторного поля скоростей свободных носителей заряда. Векторное поле скоростей в неоднородном проводнике также неоднородно.

Ток через площадку будет равен скалярному произведению этого вектора на вектор : . Для нахождения тока в проводнике вычисляем интеграл по поверхности, пересекающей проводник:

. (11.2)

Для того чтобы наши дальнейшие рассуждения были обоснованными, нам нужно оценить скорость направленного движения свободных носителей заряда. Пусть у нас есть медный проводник с площадью поперечного сечения 1 мм², в котором течет ток 1А. Для оценки будем считать концентрацию свободных электронов равной концентрации атомов меди: . Тогда для скорости направленного движения электронов получим .

Теперь вернемся к определению векторного потенциала, который создают движущиеся заряды в куске проводника с током. Во многих задачах этот кусок проводника с током можно полностью охарактеризовать вектором , зная ток в нем (рис.11.2). Этого бывает достаточно, если характеристический размер сечения много меньше расстояния от этого куска проводника до точки в пространстве, где мы определяем электрическое поле^*. Удаление куска проводника от точки в пространстве, определяемой радиус-вектором , где определяем векторный потенциал, обозначим , причем . Здесь - радиус-вектор куска проводника с током.

Пусть в нашем проводнике концентрация, скорость направленного движения положительных и отрицательных свободных носителей и их заряды одинаковы ^**, тогда суммарный заряд в куске проводника равен нулю и скалярный потенциал в любой точке пространства будет равен нулю.

Рис.11.2

Векторный же потенциал в соответствии с принципом суперпозиции (10.6) будет равен:

.

Для отыскания векторного потенциала электрического поля, созданного движущимися носителями во всем проводнике необходимо вычислить интеграл по контуру , который совпадает с проводником:

. (11.3)

Если выше сформулированное условие ^* не выполняется, то необходимо вычислять интеграл по всему объему с движущимися зарядами:

, (11.4)

где - плотность тока в объеме , - удаление объема до той точки в пространстве, где мы определяем поле.

Теперь рассмотрим не исключительный случай ^**, а более важный для практических задач случай металлического проводника с током. Если в нем поле отсутствует, средняя скорость направленного движения и положительных и отрицательных зарядов равна нулю, объемная плотность заряда проводника (и линейная плотность , если проводник – тонкая проволока) равна нулю. Электрического поля в окружающем пространстве заряды в проводнике не создают. Если в металлическом проводнике появляется поле, то свободные электроны в нем приходят в упорядоченное движение, положительные заряды остаются неподвижными. Векторный потенциал определяется также выражениями (11.3), (11.4). Отметим, что его появление – релятивистский эффект линейный по параметру . Скалярный потенциал вблизи проводника с током также оказывается не равным нулю, поскольку для движущихся зарядов наблюдается лоренцево сокращение расстояния между ними и линейная плотность заряда проводника оказывается равна:

.

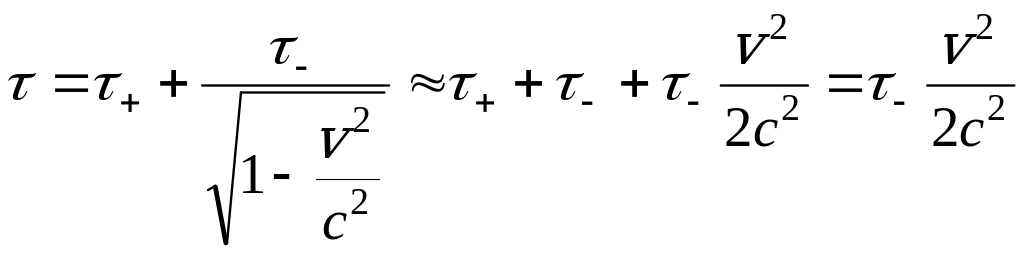Второе слагаемое мы разложили в ряд Тейлора по малому параметру . Видно, что появление скалярного потенциала в этом случае – релятивистский эффект второго порядка малости. Для тех скоростей направленного движения носителей заряда в проводниках, которые соответствуют реальным плотностям тока, всеми эффектами второго порядка можно пренебречь.

Подводя итоги, можно сказать, что электрическое поле вблизи проводников с токами можно характеризовать только векторным потенциалом, определяемым соотношениями (11.3), (11.4), считая скалярный потенциал всюду равным нулю.