Определение предела функции

Определение предела функции по Гейне.

Пусть f(x) определена в некоторой окрестности точки х₀ за исключением может быть точки х₀.

Число А-предел ф-ии f(x) в точке х₀.

Если для любой последовательности Х₁,Х₂,Х₃,…Х_n ,сходящиеся в точке х₀ при n ∞ lim Х_n= Х₀ , то выполняется условие:

Последовательность значений ф-ий f(Х_n) имеет предел А.

4.Односторонние пределы. Необходимые и достаточные условия существования предела. Геометрический смысл предела.

Геометрический смысл предела

На рис. 6 изображены окрестности и в случае предела

.

Рис. 6

На рис. 7 для случая предела изображена -окрестность числа b и такое число N(), что если x > N(), то соответствующие значения функции попадают в -окрестность числа b и не покидают ее никогда.

Рис. 7

Односторонние пределы. Необходимое и достаточное условия существования предела функции

	 называется правосторонним пределом функции f(x) в точке или пределом справа.
	 называется левосторонним пределом функции f(x) в точке или пределом слева.

Теорема 1.1. Для того, чтобы существовал предел функции , необходимо и достаточно чтобы существовали односторонние пределы функции равные между собой, т. е.

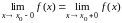
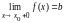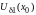Достаточность. Пусть существуют равные между собой односторонние пределы и . Тогда в случае для любого  > 0 существует окрестность такая, что  x>  значение f(x)  . Также в случае 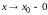для того же  > 0 существует окрестность такая, что  x <  значение f(x)  . Тогда для заданного значения  > 0 при , х значение функции f(x)  независимо от того x > или x < , т. е. предел существует.

5.Определение предела функции непрерывного аргумента по Коши при х —> х ₀ и х —> ∞.

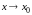Определение предела функции по Коши. Число a называется пределом в т. (при ) ( ), если для любого >0 существует ()>0, такое что для всех х |х- |< выполняется условие | .

Определение предела функции при . Число b называется пределом функции при ( ), если для любого положительного числа  существует такое положительное число N, зависящее от , что если значение > N, то значение функции принадлежит -окрестности числа b ( ).

Кратко с помощью кванторов можно записать

.

Аналогично могут быть сформулированы определения предела функции пр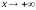и и , а именно

;

.

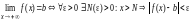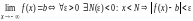6.Бесконечно малые и бесконечно большие функции, взаимосвязь между ними. Свойства бесконечно малых функций.

Определение бесконечно малой функции. Функция 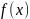имеющая предел в т. называется бесконечно малой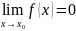

Определение бесконечно большой функции. Функция называется бесконечно большой при , если для любого N>0 существует такое положительное число , что для всех х, удовлетворяющих неравенству 0<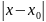 < 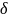, выполняется неравенство . т.е. .

Функция, обратная по величине к бесконечно малой функции является бесконечно большой и, наоборот, функция, обратная по величине к бесконечно большой, является бесконечно малой функцией.