
- •1.Множества, способы их задания. Модуль числа, его свойства. Грани множеств. Счетные и несчетные множества.
- •2.Функции, способы их задания, классификация.
- •3.Окрестность точки. Предел последовательности. Теоремы Больцано-Коши и Вейерштрасса (без доказательства). Определение предела функции по Гейне.
- •Определение предела функции
- •4.Односторонние пределы. Необходимые и достаточные условия существования предела. Геометрический смысл предела.
- •Односторонние пределы. Необходимое и достаточное условия существования предела функции
- •6.Бесконечно малые и бесконечно большие функции, взаимосвязь между ними. Свойства бесконечно малых функций.
- •Свойства бесконечно малых функций
- •7.Теоремы о представлении функции в виде суммы предела и бесконечно малой функции. Теоремы о пределах (свойства пределов).
- •Теоремы о пределах (свойства пределов)
- •8.Теорема о промежуточной функции. Первый замечательный предел.
- •Замечательные пределы
- •Первый замечательный предел
- •Следствия из первого замечательного предела:
- •9.Второй замечательный предел, его обоснование.
- •10.Сравнение бесконечно малых функций.
- •11.Непрерывность функции в точке и на отрезке. Действия над непрерывными функциями. Непрерывность основных элементарных функций.
- •12.Свойства непрерывных функций.
- •13.Точки разрыва функций.
- •Классификация разрывов
- •14.Производная функции, ее геометрический и физический смысл.
- •Физический смысл производной
- •15.Взаимосвязь непрерывности и дифференцируемости функции. Непосредственное нахождение производной.
- •Непосредственное нахождение производной
- •16.Правила дифференцирования функций.
- •17.Вывод формул дифференцирования основных элементарных функций.
- •19.Вывод формул дифференцирования степенной и показательно-степенной функций. Таблица производных. Производные высших порядков.
- •Производные высших порядков
- •21.Дифференциал функции одной переменной. Определение, условия существования, геометрический смысл, свойства.
- •Свойства дифференциала
- •22.Применение дифференциала функции одной переменной для приближенных вычислений. Дифференциалы высших порядков.
- •23.Теорема Ролля, её геометрический смысл, примеры её использования.
- •Пример:
- •24.Теорема Лагранжа о конечном приращении функции, её геометрический смысл.
- •25.Теорема Коши о дифференцируемых функциях.
- •26.Правило Лопиталя, его использование для раскрытия неопределенностей при нахождении пределов.
- •Применение правила Лопиталя для раскрытия неопределенностей типа степени
- •27.Формула Тейлора. Остаточный член в форме Лагранжа.
- •28.Формула Маклорена, её остаточный член. Разложение элементарных функций.
- •Разложение основных элементарных функций по формуле Маклорена
- •30.Монотонные функции. Необходимый и достаточный признаки монотонности функции.
- •31.Локальный экстремум функции. Необходимый признак экстремума функции.
- •32.Первый и второй достаточные признаки экстремума функции.
- •33.Достаточный признак выпуклости, вогнутости графика функции.
- •Достаточный признак выпуклости, вогнутости графика функции
- •34.Необходимый и достаточный признаки существования точки перегиба. Необходимый признак существования точки перегиба
- •Достаточный признак существования точки перегиба
- •35.Асимптоты графика функции. Общая схема исследования функции и построения графика.
- •Общая схема исследования функции и построения графика.
- •36.Функция нескольких переменных, се определение, линии уровня и поверхности уровня.
- •37.Определение предела функции нескольких переменных по Коши. Свойства пределов.
- •38.Бесконечно малые функции.Определения непрерывности функции нескольких переменных. Свойства непрерывных функций.
- •40.Необходимые условия дифференцируемости функции нескольких переменных. Примеры взаимосвязи дифференцируемых и непрерывных функций.
- •41.Достаточные условия дифференцируемости функции нескольких переменных.
38.Бесконечно малые функции.Определения непрерывности функции нескольких переменных. Свойства непрерывных функций.
Функция
нескольких переменных называется бесконечно
малой,
если ее предел равен нулю.
 =0
=0
Определение.
Функция
 называется непрерывной в точке
,
если
=
называется непрерывной в точке
,
если
= или
=
или
= ).
Основные
свойства непрерывных функций двух
переменных
1.Теорема 1
Если
функция
).
Основные
свойства непрерывных функций двух
переменных
1.Теорема 1
Если
функция
 непрерывна в замкнутой ограниченности,
то она ограничена в этой области.
2.Теорема
2
Если
функция
непрерывна в замкнутой ограниченности,
то она достигает в этой области своих
точных верхней и нижней граней(аналог
второй теоремы Вейерштрасса).
3.Теорема
3
Если
функция
непрерывна в замкнутой ограниченности,
то она принимает все промежуточные
значения между любыми своими значениями
A
и B,
т.е.
если A
непрерывна в замкнутой ограниченности,
то она ограничена в этой области.
2.Теорема
2
Если
функция
непрерывна в замкнутой ограниченности,
то она достигает в этой области своих
точных верхней и нижней граней(аналог
второй теоремы Вейерштрасса).
3.Теорема
3
Если
функция
непрерывна в замкнутой ограниченности,
то она принимает все промежуточные
значения между любыми своими значениями
A
и B,
т.е.
если A и A
и B-два
значения функции
и A
и B-два
значения функции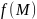 ,
то
т.(
;
,
то
т.(
;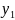 ),
т.ч.
;
)=C(аналог
теоремы Больцано-Коши).
Следствие
из теоремы
Если
),
т.ч.
;
)=C(аналог
теоремы Больцано-Коши).
Следствие
из теоремы
Если
 ,
а
,
а
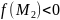 ,
то
,
то
 ,
т.ч.
=0,
,
,
т.ч.
=0,
,
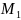 ,
,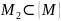 .
.
39. Частные приращения и частные производные функции нескольких переменных.Правило нахождения частных производных. Геометрический смысл частных производных.
Для
функции
 частными приращениями по х
и по y
называется соответственно
частными приращениями по х
и по y
называется соответственно
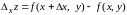 ,
,
 .
.
Частной производной функции нескольких переменных по некоторой переменной называется предел отношения частного приращения функции по этой переменной к приращению переменной, стремящемуся к нулю, т. е.
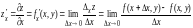 ,
,
 .
.
Для
функции
не имеют смысла записи
 или
или
 .
.
Не
существует просто производная функции
,
а существуют только частные производные
по х
и по y,
обозначаемые
 и
и
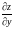 .
.
40.Необходимые условия дифференцируемости функции нескольких переменных. Примеры взаимосвязи дифференцируемых и непрерывных функций.
ОПРЕДЕЛЕНИЕ.
Функция
 называется дифференцируемой в точке
называется дифференцируемой в точке
 если ее полное приращение в этой точке
может быть записано в виде
если ее полное приращение в этой точке
может быть записано в виде
 , (4.1)
, (4.1)
где
 – некоторые числа,
– некоторые числа,
 – бесконечно малые при
– бесконечно малые при
 ,
,
 (или, короче при
(или, короче при
 ).
).
Замечание.
Функции
 и
и
 зависят от
зависят от
 .
.
Функция , дифференцируемая в каждой точке некоторой области, называется дифференцируемой в этой области.
ТЕОРЕМА 4.1. (необходимые условия дифференцируемости).
Если
функция
дифференцируема в точке
,
то она непрерывна в этой точке и имеет
в ней частные производные по обеим
независимым переменным. Причем
 ,
а
,
а
 .
.
ДОКАЗАТЕЛЬСТВО…
1)
Пусть
 дифференцируема в точке
.
Значит ее приращение в этой точке может
быть записано в виде
дифференцируема в точке
.
Значит ее приращение в этой точке может
быть записано в виде
, (*)
где – некоторые числа, – бесконечно малые при , . Тогда
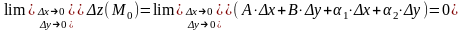 .
.
С другой стороны,

 .
.
Следовательно,
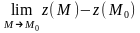
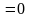 ,
,
⇒
 ,
,
т.е. непрерывна в точке .
2)
Пусть
 .
Тогда формула (*) примет вид
.
Тогда формула (*) примет вид
 ,
,
где
 – некоторое число,
– бесконечно малая при
,
.
Отсюда получаем:
– некоторое число,
– бесконечно малая при
,
.
Отсюда получаем: 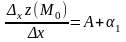
и
 .
.
Аналогично
доказывается, что существует
 .
∎
.
∎
С
учетом теоремы 4.1 равенства (4.1) и (4.2)
можно теперь записать в виде  (4.3)
(4.3)
 (4.4)
(4.4)
где
– бесконечно малые при
,
,
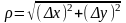 ,
,
 – бесконечно малая при
– бесконечно малая при
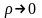 .
.
Утверждение обратное теореме 4.1 неверно. Из непрерывности функции двух переменных в точке и существования в этой точке ее частных производных еще не следует дифференцируемость функции.
ТЕОРЕМА 4.2. (достаточные условия дифференцируемости).
Если
функция
имеет в некоторой окрестности точки
частные производные
 и
и
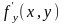 ,
причем в самой точке
,
причем в самой точке
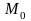 эти производные непрерывны, то функция
дифференцируема в этой точке.
эти производные непрерывны, то функция
дифференцируема в этой точке.
ПРИМЕР.
1) Функция
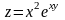 в любой точке
в любой точке
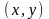 дифференцируема, так как ее частные
производные
дифференцируема, так как ее частные
производные
 и
и
 всюду непрерывны.
всюду непрерывны.
2)
Функция
 дифференцируема в каждой точке
полуплоскости
дифференцируема в каждой точке
полуплоскости
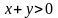 ,
так как там существуют и непрерывны ее
частные производные
,
так как там существуют и непрерывны ее
частные производные
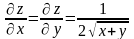 .
.
И в заключение этого пункта заметим, что все определения и теоремы, которые мы здесь формулировали, легко переносятся на случай функций большего числа переменных.
