Оглавление

1.Множества, способы их задания. Модуль числа, его свойства. Грани множеств. Счетные и несчетные множества.

Множество-совокупность однородных объектов. Элементы множества-объекты, из которых состоит множество. Множества обозначаются прописными буквами, а элементы множества строчными буквами. Элементы множеств заключаются в фигурные скобки.

 Существуют два основных способа задания множеств: перечисление и описание его элементов. Перечисление состоит в получении полного списка элементов множества, а описание заключается в задании такого свойства, которым элементы данного множества обладают, а все остальные нет. 

Определение модуля

Модуль действительного числа — это абсолютная величина этого числа. Модулем неотрицательного действительного числа x называют само это число.

Модулем отрицательного действительного числа x называют противоположное число.

| |=

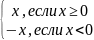
Свойства модуля

1. Модули противоположных чисел равны	| |=| |
2. Квадрат модуля числа равен квадрату этого числа	=
3. Квадратный корень из квадрата числа есть модуль этого числа	=| |
4. Модуль числа есть число неотрицательное	| | 0
5. Постоянный положительный множитель можно выносить за знак модуля	|c |= c | |, c
6. Если | |=|𝑏|, то	= 𝑏
7. Модуль нуля равен нулю	| |=
8.Модуль произведения двух (и более) чисел равен произведению их модулей	| 𝑏|=| 𝑏|
9.Модуль частного двух чисел(если делитель отличен от нуля) равен частному модулей этих чисел	| |= ,

Числовым множеством является множество, элементами которого являются вещественные числа. Наиболее распространенные числовые множества: · N – множество натуральных чисел;

· Z – множество целых чисел;

· Q – множество рациональных или дробных чисел;

· I – множество иррациональных чисел

Грани числовых множеств Множество X называется ограниченным сверху(снизу), если существует( ) число с(с’), т.ч. для x X выполняется условие x c(x c’). Число К называется верхней гранью множества А, если .

Если С > 0, то К + С также является верхней гранью этого множества.

Число k называется нижней гранью множества А, если . Если С > 0, то k  С также является нижней гранью этого множества.

Среди множества верхних граней K + С множества А существует наименьшая верхняя грань M, которая называется точной верхней гранью или «супремум» М = sup (A). Также среди множества нижних граней k  С для множества А существует наибольшая нижняя грань m, которая называется точной нижней гранью или «инфимум» m = inf (A).

Например: 1) если А = [0; 1], то sup (A) = 1, inf (A) = 0; 2) если А = (0; 1), то sup (A) = 1, inf (A) = 0.

Счетные и несчетные множества

Для того, чтобы сравнить два каких-либо множества А и В, между их элементами устанавливают соответствие.

Если это соответствие взаимнооднозначное, то множества называются эквивалентными или равномощными, А  В или А  В.

Примеры: 1. Множества А = {1, 2, 3, …, n, …} и являются равномощными, т. к. между их элементами можно установить взаимнооднозначное соответствие: 1  , 2  , 3  , …, n  , ….

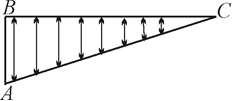
2. Множество точек катета BC и гипотенузы AC треугольника ABC являются равномощными.

Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров .

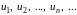Счетным множеством называется множество эквивалентное множеству натуральных чисел.

Следовательно, любая последовательность является счетным множеством.

Предложение 1. Для того, чтобы множество было счетным, необходимо и достаточно, чтобы его можно было представить в виде последовательности.

Предложение 2. Декартово произведение конечного или счетного числа счетных множеств является счетным множеством.

Предложение 3. Любое подмножество счетного множества является либо конечным, либо счетным.

Таким образом, счетное множество является наименее мощным из бесконечных множеств.

Более мощным, чем счетное множество, является множество действительных чисел 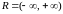. Его мощность называют мощностью континуума. Так как [0; 1]  R, то множество точек отрезка [0; 1] обладает также мощностью континуума.