3. Примеры решения задач

Здесь будут рассмотрены задачи на составление модели операции и оценку эффективности стратегии.

Составление модели операции состоит в определении множества Х- стратегий ОС, множества Y- неопределенных факторов, множества Z и функции распределения (z) случайных факторов z и в определении критерия операции f(x, у, z) исходя из цели операции.

Задача 1 Скорость движения машин в автомобильном туннеле не превышает 50 км/ч и связана с плотностью потока ( количеством машин на километр дороги ) р следующим эмпирическим соотношением

Р = , где v₀ = 60 км/ч, a z- случайная величина, которая в любой момент определяется отношением грузовых и легковых машин, проходящих через туннель. Известно, что величина z распределена равномерно на отрезке [0.5;1]. Регулировка движения в туннеле производится выбором скорости движения v. За проезд по туннелю с легковой машины взимается плата денежных единиц, а с грузовой - (0< < ). Цель операции состоит в получении максимальной платы за 1 час работы туннеля. Требуется составить математическую модель операции и определить оценку эффективности произвольной стратегии ОС.

Решение. Контролируемым фактором х является скорость движения v по туннелю. Множество X контролируемых факторов по условию задачи определяется соотношением

X={x: 0 x 50}.

Неконтролируемым фактором является случайная величина z Z =[0.5;1] с равномерным законом распределения:

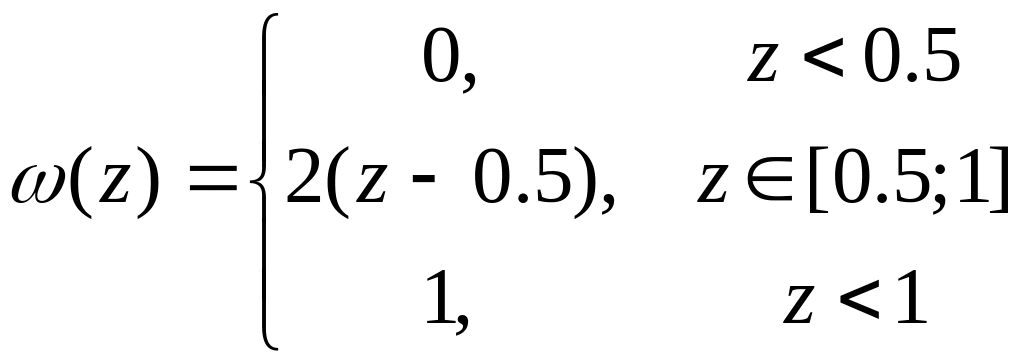
Неопределенных неконтролируемых факторов нет (Y= ).

Критерием операции является количество денег, полученных в течение часа. Так как плата взимается при въезде в туннель, то для определения этой величины найдем количество С(x,z) машин, въезжающих в туннель за один час, при заданных величинах (х, z).

С(x, z)=x P=

Найдем, сколько среди них грузовых и легковых. Так как

z= ,

где - количество грузовых машин, a g- количество легковых машин, то

g= ; =

Следовательно:

f(x,z): .

Итак, все компоненты математической модели {X, Y, (Z, (z)), f} определены.

Оценим эффективность произвольной стратегии х. Рассмотрим только два критерия эффективности:

1) критерий ожидаемого значения, т. е. ОС допускает осреднение;

2)критерий наилучшего гарантированного результата, то есть ОС предполагает, что величина z будет реализовываться наихудшим для нее образом.

В случае 1) по формуле (11) получаем

Дифференцируя по x и приравнивая к нулю, получаем, что по этой оценке лучший результат достигается при x⁰=30км/ч.

В случае 2) ОС считает z неопределенным фактором и никак не использует информацию о случайном его характере (о функции распределения вероятностей). Полагая в формуле (3) y=z, Y=Z получаем

Так как функция монотонно убывает при z 0, то на отрезке [0.5; 1] она принимает минимальное значение в точке x=1, следовательно,

.

Максимум этой функции достигается в точке x⁰=30км/ч.

Задача 2

В мэрии рассматриваются три проекта строительства теплопунктов в новом микрорайоне. Затраты по строительству, обслуживанию и развитию в соответствии с четырьмя возможными вариантами развития микрорайона заданы в виде таблицы

10	15	17	9
14	12	10	16
12	13	14	15

Найти проект, минимизирующий затраты.

Решение. Контролируемым фактором является выбор того или иного проекта. Обозначим x_i – выбор i-го проекта, тогда X={x₁, x₂, x₃,} – множество контролируемых факторов. Неконтролируемым фактором будет вариант развития микрорайона. Обозначим y_j – j-й вариант развития микрорайона, тогда Y={y₁, y₂, y₃, y₄} – множество неконтролируемых факторов. Так как не задано вероятностей наступления y_j , то это неопределенный фактор. Целевая функция задана в виде таблицы. Найдем решения по четырем критериям в условиях неопределенности. Напомним, что по условиям задачи ОС необходимо минимизировать затраты.

1. В соответствии с критерием Вальда (3)

W₁(x₁)=max{10; 15; 17; 9}=17;

W₁(x₂)=max{14; 12; 10; 16}=16;

W₁(x₃)=max{12; 13; 14; 15}=15.