2. Оценка эффективности стратегий

Для выбора некоторой стратегии ОС должна иметь возможность оценить насколько она хороша или плоха. Так как результаты операции оцениваются критерием операции, то и оценка эффективности основывается на этой функции. Оценки эффективности могут быть различными в зависимости как от информации, которой обладает ОС, так и от субъективных решений ОС.

В случае принятия решения в условиях определенности критерий операции имеет вид f: X R, т.е. зависит только от контролируемых факторов, характеризует достижение цели одним числом, и при этом наибольшему достижению цели соответствует максимальное (минимальное) значение функции f. Тогда оптимальной будет такая стратегия x_* Х, которая доставляет максимум (минимум) функции f;

f(x_*)= .

В случае, когда в операции присутствуют неконтролируемые факторы (Y , Z ) ОС оценить свою стратегию становится значительно труднее. Существует несколько разумных способов оценки стратегий и ОС необходимо выбрать один из них, либо некоторую комбинацию критериев.

2.1. Оценка эффективности стратегий в условиях неопределенности

Рассмотрим случай, когда Z , то есть нет случайных факторов, и m= 1

f: X Y R.

Тогда наиболее распространенными являются следующие способы оценки эффективности стратегий.

2.1.1. Принцип наилучшего гарантированного результата (критерий Вальда). Предполагается, что для каждой стратегии х X ОС будет реализовываться наиболее плохой для ОС неопределенный фактор у Y. Так, если цель ОС максимизировать «выигрыш» f(x,y), то любая стратегия х X оценивается величиной

(3)

Оценку W₁(х) (3) называют еще оценкой крайнего пессимизма. Таким образом, в рассматриваемом случае величина W₁(x) оценивает «выигрыш» ОС снизу, то есть, выбрав стратегию х X, ОС получит «выигрыш» f(x,y) не меньший, чем W₁(x), какое бы у Y не реализовалось. Иными словами, при применении стратегии х ОС гарантировано получит выигрыш не меньший величины W₁(х). Оптимальной по этому критерию будет стратегия x₀, доставляющая максимум функции W₁(х) на множестве X.

.

Применение принципа наилучшего гарантированного результата обосновано, когда выбор неопределенного фактора у Y осуществляет разумный противник, ставящий своей целью уменьшение «выигрыша» ОС.

В случае, когда ОС стремится минимизировать величину f(x,y), вместо оценки W₁(x) (3) применяется аналогичная оценка

Соответственно

.

Если ОС не противостоит разумный противник, применение принципа наилучшего гарантированного результата может показаться сильно «пессимистичным». В этих случаях говорят об «играх с природой». Неконтролируемые факторы выбирает «природа», основываясь на своих, неизвестных ОС, целях. Однако, нет оснований предполагать, что «природа» старается навредить ОС. Наиболее известными в данной ситуации являются критерии Лапласа, Сэвиджа и Гурвица.

2.1.2. Критерий Лапласа. Этот критерий основывается на следующем принципе недостаточного обоснования. Поскольку распределение вероятностей на неопределенных факторах неизвестно, то принимаем, что это распределение является распределением равномерного закона.

Еще раз напомним, что в рассматриваемых случаях ОС не противостоит разумный противник, который выбирает неконтролируемый фактор с целью максимально ухудшить результат операции для ОС.

Критерий Лапласа оценивает стратегию х X величиной математического ожидания выигрыша ОС при равномерном законе распределения вероятностей неконтролируемых факторов. Оптимальной по этому критерию считается стратегия, доставляющая максимум (если нужно максимизировать целевую функцию) математическому ожиданию целевой функции

, . (4)

Здесь – функция плотности распределения вероятностей равномерного закона; p_i – вероятность того, что неконтролируемый фактор примет значение y_i . При этом

p_i=1/i.

Первая формула применяется в случае непрерывной случайной величины y. Вторая формула для конечного множества Y={y₁,…,y_m}.

Пример 3. Предприятие должно определить уровень предложения услуг так, чтобы удовлетворить потребность клиентов в течение предстоящих праздников. Точное число клиентов неизвестно, но оно может принимать одно из четырех значений: y₁=200, y₂=250, y₃=300, y₄=350. Для каждого из этих возможных значений существует наилучший уровень предложения (x_1,…,x₄) с точки зрения минимизации затрат. Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса (дополнительные расходы из-за необходимости срочных закупок, упущенная прибыль).

Значения затрат в зависимости от уровня услуг и возможного числа клиентов заданы в виде таблицы. По критерию Лапласа события y₁, y₂, y₃, y_4. равновероятны. Следовательно, для любого i вероятность

	y1	y2	y3	y4	того, что произойдет событие yi, равно 0.25.
x1	5	10	18	25	В этом случае ожидаемые затраты при раз-
x2	8	7	8	23	личных уровнях предложения услуг соста-
x3	21	18	12	21	вят соответственно:
x4	30	22	19	15	M{x1}=0.255+0.2510+0.2518+0.2525=14.5;

M{x₂}=11.5; M{x₃}=18.0; M{x₄}=21.5. Наилучшим уровнем предложения услуг в соответствии с критерием Лапласа будет x₂.

2.1.3. Критерий Сэвиджа. Рассмотрим следующий пример. Пусть множества X={x₁, x₂} и Y={y₁, y₂} состоят только из двух элементов. Целевая функция является функцией затрат ОС и задана таблицей. Приме-

	y1	y2	max	нение критерия наилучшего гарантирован-
x1	1010	9	1010	ного результата дает в качестве решения
x2	1000	1000	1000	стратегию x2. Однако, если ОС применит

Стратегию x₁, то при худшем для него варианте y=y₁ затраты возрастут по сравнению с гарантированным результатом на 1%, а при благоприятном варианте затраты составят только 0.9% от гарантированных затрат, т.е. уменьшатся на 99.1%.

Учесть подобные ситуации и реализовать выбор стратегии, дающей возможно небольшой проигрыш, но и возможно существенный выигрыш по сравнению со стратегией гарантированного результата, позволяет критерий Сэвиджа. Пусть целевая функция f(x,y) есть функция выигрыша ОС. Следовательно, ОС стремится максимизировать целевую функцию. Составим функцию сожаления:

(5)

Величина выражает «сожаление» ОС в том, что она для данного неопределенного фактора y выбрала стратегию x, а не лучшую стратегию

.

Функцию называют также функцией риска. Затем для функции применяется критерий наилучшего гарантированного результата, то есть оптимальное х₀ ищется следующим образом. Для каждого контролируемого фактора х X

. (6)

В случае, когда в модели операции задана функция потерь (проигрыша), функция сожаления будет иметь вид

(7)

и опять выражает «сожаление» ОС о том, что она для данного неопределенного фактора y Y применила стратегию x, a не лучшую стратегию :

.

Далее, оптимальная по данному критерию стратегия х₀ ищется из критерия наилучшего гарантированного результата для ₂(х, у):

.

Функция сожаления и в случае функции выигрыша f (формула (5)) и в случае функции потерь f (формула (7)) выражает величину потерь ОС от неприменения лучшей стратегии. Поэтому критерий наилучшего гарантированного результата в обоих случаях является минимаксным:

(8)

Составим матрицу сожаления для приведенного в начале пункта примера. Так как функция f(i, j) в данном примере есть функция потерь, то

Функцию ₂(i, j) запишем в виде матрицы S сожалений:

S=

Теперь из критерия наилучшего гарантированного результата для матрицы S получаем, что оптимальной будет стратегия х_1.

Рассмотрим пример 3. Так как в этом примере задана функция потерь, то функция сожаления (i, j) вычисляется по формуле (7).

=5-5=0, , ₂(1,3)=21-5=16 и т. д.

Результаты вычислений запишем в виде матрицы S:

S

=

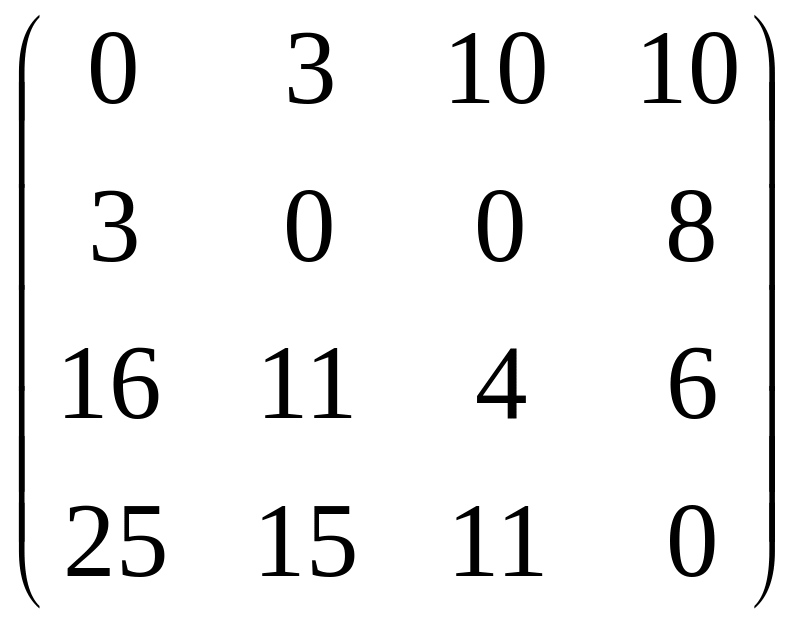
Для нахождения оптимальной по критерию Сэвиджа стратегии ОС найдем по матрице сожалений S стратегию х₀, удовлетворяющую принципу наилучшего гарантированного результата. Для этого в силу (8) нужно найти максимальный элемент в каждой строке матрицы S. Обозначим его b₁, b₂, b₃, b₄, соответственно. Затем необходимо найти наименьшее из чисел b_i. Тогда номер i^*: b_i*= min{b_j}- определит оптимальную стратегию. В примере 3 b₁=10, b₂=8, b₃=16, b₄=25. Соответственно, i₀ =2, так как b₂=min{b₁;b₂;b₃;b₄}. Следовательно, стратегия х₂ является оптимальной по критерию Сэвиджа в данном примере. Этот ответ совпадает с ответом, полученным по критерию Лапласа.

Таким образом, для приведенной в примере 3 функции потерь оптимальной и по критерию Лапласа, и по критерию Сэвиджа является стратегия х₂. Однако из приведенного примера не стоит делать вывод, что такое совпадение будет всегда выполняться. Можно привести пример, когда эти два критерия будут считать оптимальными различные стратегии.

2.1.4. Критерий Гурвица. Для определения следующего критерия нам понадобится понятие выпуклой комбинации.

Определение 13. Число с называется выпуклой комбинацией чисел a и b, если существует число [О;1] такое, что

c= a +(1 - ) b.

Отметим, что множество всех таких чисел образует отрезок [a ; b]. Критерий Гурвица является выпуклой комбинацией критериев крайнего пессимизма W₁(x, у) и крайнего оптимизма:

. (9)

Здесь мы считаем, что задана функция выигрыша f(x, y). Критерий крайнего оптимизма предполагает, что неопределенный фактор y Y - максимально содействует ОС в ее стремлении увеличить свой выигрыш. Итак, в случае, когда задана функция выигрыша f(x, y) ОС критерий Гурвица имеет вид:

= . (10)

Оптимальной в этом случае считается стратегия х₀ X, доставляющая максимум функции W₅(x), т.е.

W₅(х₀)= W₅(x) .

Для функции потерь (х, у) критерий Гурвица задается равенством:

W₆ (x)= . (11)

Оптимальной при этом считается стратегия х₀ X, на которой достигается минимум функции W₆(х), т. е.

W₆ (x₀)= W₆ (x).

Параметр называется показателем оптимизма: при =1 критерий Гурвица превращается в критерий крайнего оптимизма, при =0 – в критерий крайнего пессимизма. Выбор параметра осуществляется ОС, исходя из ее взглядов на данную операцию, то есть является субъективным.

Найдем решение задачи из примера 3 по критерию Гурвица в случае = 0.2. Имеем соответственно:

W₆(x₁) = [0.2min{5; 10; 18; 25} + mах08{5; 10; 18; 25}] = 0.25 + 0.825 = 21,

W₆(x₂) = [0.27 + 0.823] =19.8, W₆(x₃) = [0.212 + 0.821] = 19.2,

W₆ (х₄) = [0.215 + 0.830] = 27.

Анализируя зависимость выбора оптимальной стратегии от значения , получим:

(0.5; 1] – оптимальная стратегия х₁;

=0.5 – оптимальные стратегии х₁ и х₂;

(2/7; 0.5) – оптимальная стратегия x₂;

= 2/7 – оптимальные стратегии x₂ и х₃;

[0; 2/7) – оптимальная стратегия х₃.

Таким образом, в зависимости от выбранной величины оптимизма ОС может получить различные ответы об оптимальности стратегии.