- Шығыстық шаманың кескіні,

-кірістік шаманың кескіні.

3. Өтпелі функция h(t) деп жүйенің бастапқы нөлдік шартқа сәйкес кірісіне берілген бірлік секіріске деген реакциясын айтады.

Сурет 3.1 Өтпелі функция сызбасы

Өтпелі функцияны дифференциал теңдеуді шешу арқылы немесе эксперементаль әдіспен анықтайды.

Өтпелі функцияның графигіндегі кескінін – екпін қисығы дейміз.

4. Импульсті өтпелі функциясы- W(t) жүйенің кірісіне бастапқы нөлдік шартқа сәйкес берілген бірлік импульсқа (дельта функция) деген реакцияны айтады. Импульсті беріліс функциясын W(t)беріліс

5. Жиіліктік және логарифмдік жиіліктік сипаттамалар

Жиіліктік сипаттамалардың негізінде автоматтв жүйелерді зерттеудің біршама инженерлік тәсілдері дамыған. Жиіліктік сипаттамалардың ерекшелігі, олар жүйенің динамикалық қасиеттеріне жүйе параметрлерінің тигізетін әсерлерін бағалауға мүмкіндік береді. Сонымен қатар бұл сипаттамаларды тәжрибе жүзінде де алуға болады.

Жиіліктік сипаттамалар жүйелердің кірісене гармоникалық сигнал берілген жағдайдағы жүйе шығысының еріксіз тербелісін сипаттайды да, жүйелердің комплекстік беріліс функцияларының (КБФ) негізінде тұрғызылады. Егер жүйе кірісіне гармоникалық тербеліс берілсе, онда өтпелі процесс аяқталған соң жүйе шығысында амплитудасы және бастапқы фазасы кірістік тербелістен өзгеше, ал жиіліктері бірдей тұрақталған гармоникалық еріксіз тербеліс аламыз.

Комплекстік беріліс функциясы W(j ) деп, тұрақталған режимдегі жүйенің комплексті түрде көрсетілген шығыстық шамасының комплексті түрде көрсетілген кірістік шамасына қатынасын айтады.

, мұндағы және шығыстық және кірістік шамалардың комплекстері . Егер жүйе кірісіне синусоидалы сигнал берілсе , онда өтпелі процесс аяқталған мезетте жүйе шығысында да синусоидалы сигнал пайда болады .

Синусоидалы сигналдарды комплекстік түрге келтірсек

;

Бұдан жүйенің КБФ мынаған тең

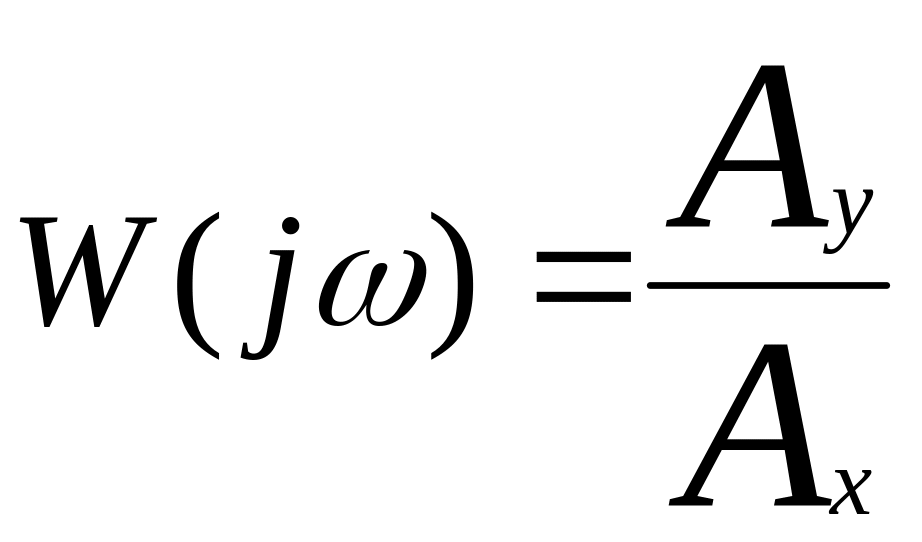. e ^{j(φ - φ )} = A( ) · e ^jφ(ω) (3.1)

мұнлағы 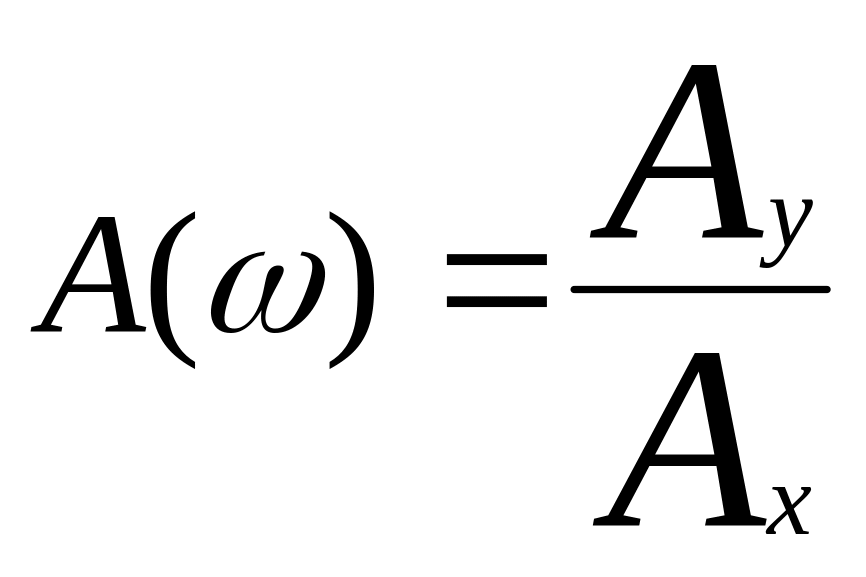–КБФ-ың модульі, φ(ω) = φ_y – φ_x – КБФ-ың аргументі.

A( ) шамасы шығыстық және кірістік амплитудалар қатынасының жиілікке тәуелділігін сипаттайды, ал φ(ω) – түрлі жиіліктегі шығыстық тербеліспен кірістік тербелістің араларындағы фазалық ығысуды сипаттайды

КБФ –ың алгебралық түрдекі жазылу нұсқасы

W (j ) = P( ) + jQ( ) (3.2)

мұндағы P( ) – КБФ-ың нақты бөлігі, Q( ) – КБФ-ың жорамал бөлігі .

A( ) , φ(ω) , P( ) және Q( ) шамаларының арасындағы байланыс

A( ) = и φ(ω) = arctg (3.3)

КБФ комплекстік жазықтықта W (j ) векторымен анықталады. Вектордың ұзындығы КБФ-ың модулімен A( ), ал бұрылу бұрышы КБФ-ың аргументімен φ(ω) анықталады. Жиілік 0-ден -ке дейін өзгергенде, W (j ) векторының ұшы комплекс жазықтықта годограф сызады (3.1 сурет). Сызылған годографты КБФ-ың амплитудалық фазалық жиіліктік сипаттамасы (АФЖС) дейді. КБФ-ы модулінің A( ) жиілікке тәуелділігін амплитудалық жиіліктік сипаттамасы (АЖС) дейміз, ал КБФ-ы аргументінің φ(ω) жиілікке тәуелділігін фазалық жиіліктік сипаттамасы (ФЖС) дейміз.

Сурет 3.2. Годограф

Инженерлік есептеулерде логарифмдік масштабта салынған сипаттамалар кеңінен қолданылады. Логарифмдік сипаттамаларды қолданудың негізгі себептері мынада: күрделі жүйелердің АФЖС-ын тұрғызу үшін жүйеге енетін буындардың АФЖС-ын бір-бірімен көбейтуді қажет етеді. Әрине бұл күрделі операция. Егер логарифмдік сипаттамаларды қолданса, онда көбейту операцияларының орнына қосу операциялары орындалады, бұл әрине есептеу операцияларын жеңілдетеді; дәл логарифмдік сипаттамалар өздерінің асимтоталарымен (түзу кесінділермен) алмастырыла алады; логарифмдік сипаттамалар түзетуші құрылғыларды синтездеу кезінде біршама жеңілдіктер туғызады. Егер КБФ-ын логарифмдесек, алатынымыз

ln W (j ) = ln A( ) + j φ(ω) (3.4)

Соныменен логарифмдік жиіліктік сипаттама (ЛЖС) екі сипаттаманың жиынтығынан тұрады: модуль логарифмінен (нақты бөлік) ln A( ) және жорамал бөліктен j φ(ω)

Модуль логарфмінің ln A( ) логарифмдік масштабта алынған жиілікке lg тәуелтілігін логарифмдік амплитудалық жиіліктік сипаттамасы (ЛАЖС) дейміз, ал КБФ-ы аргументінің φ(ω) логарифмдік масштабта алынған жиілікке lg тәуелтілігін логарифмдік фазалық жиіліктік сипаттамасы (ЛФЖС) дейміз.

Әдетте ЛАЖС-ын тұрғызу барысында ордината өсіне ln A( ) мәнінің орнына, оған пропорционал шама L( ) = 20 lg A( ) (дБ) салынады (мұнда 20 lg A( ) = 20·0,434 ln A( )).

L( ) шамасы децибелмен өлшенеді. Децибел өлшем бірлігі жүйенің шығыстық сигналының күшейуін (баяулауын) логарифмдік масштабта сипаттап беретін өлшем. Жиіліктің логарифмдік масштабтағы өлшем бірлігі – декада. Егерде екі жиілік бір-бірінен 10 – есе айырмашылығы болса, онда ол жиіліктер өзара 1-декадаға алшақ жатыр деп есептеледі. Логарифмдік масштабты қолдану ыңғайлы болу үшін, әдетте абцисса өсіне жиілік логарифмі мәнінің орнына соған сәйкестендірілген жиіліктің өз мәні қойылады. 3.2 суретте ЛАЖС мен ЛФЖС тұрғызу мысалдары келтірілген