30. Параметрические методы изучения связи: линейный коэффициент корреляции.

Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного или нескольких факторов.

Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.

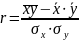
ЛКК имеет большое значение при исследовании социально-экономических явлений и процессов, распределение которых близко к нормальному. Легко доказывается, что условие r_xy=0 является необходимым и достаточным для того, чтобы величины х и у были независимы. Если r_xy=1, то это означает, что все точки (х, у) находятся на прямой и зависимость между х и у является функциональной. Линейный коэффициент корреляции изменяется в пределах от -1 до 1: -1<= r <=1.

Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза (Н₀) о равенстве коэффициента корреляции нулю.

При выполнении Н₀ t-статистика имеет распределение Стьюдента с входными параметрами: {a, k = n-2}.

Если расчетное значение t_р > t_kp (табличное), то гипотеза Н₀ отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между х и у.

Данный критерий оценки значимости применяется для совокупностей n < 50. При большом числе наблюдений (n > 100) используется следующая формула t-статистики:

Для статистически значимого линейного коэффициента корреляции можно построить интервальные оценки с помощью Z-распределения Фишера:

Оценка линейного коэффициента корреляции

Значение линейного коэффициента связи	Характер связи	Интерпретация связи
r =0	Отсутствует	-
0< r <1	Прямая	С увеличением Х увеличивается У
-1< r <0	Обратная	С увеличением Х уменьшается У
r =1	Функциональная	Каждому значению факторного признака строго соответствует одно значение результативного признака

По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи значения результативного признака изменяются в противоположном направлении по сравнению с изменением факторного признака.

Количественные критерии оценки тесноты связи

Величина коэффициента корреляции	Характер связи
До !+-0,3!	Практически отсутствует
!+-0,3! - !+-0,5!	Слабая
!+-0,5! - !+-0,7!	Умеренная
!+-0,7! - !+-1,0!	Сильная