Неопределенный интеграл.
Функция
называется первообразной функции
,
если
.
Например, для
первообразной будет функция
,
так как
.
Для функции
первообразной будет функция
,
так как
.
Заметим, что если
первообразная функции
,
то
,
где С – любое число, тоже первообразная
функции
,
так как
.
Множество первообразных функции
называется неопределенным интегралом
от функции
и обозначается
.
Например,
,
так как
Запишем таблицу неопределенных интегралов.
1)
8)
2)
9)
3)
10)
4)
11)
5)
12)
6)
13)
7)
При нахождении неопределенного интеграла используют правила:
1.
, то есть постоянный множитель выносится
за знак интеграла
2.
, то есть интеграл от суммы равен
сумме интегралов.
Пример.
По определению
Например,
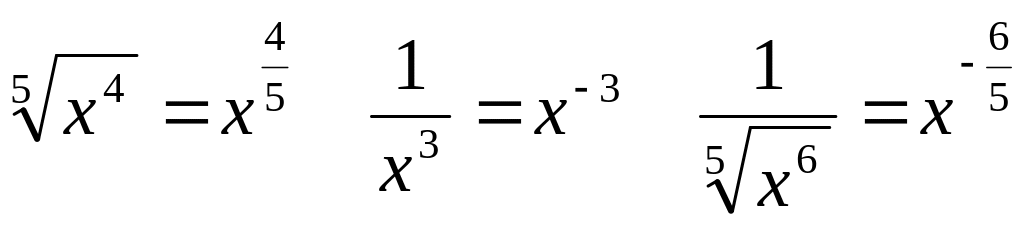
Пример.
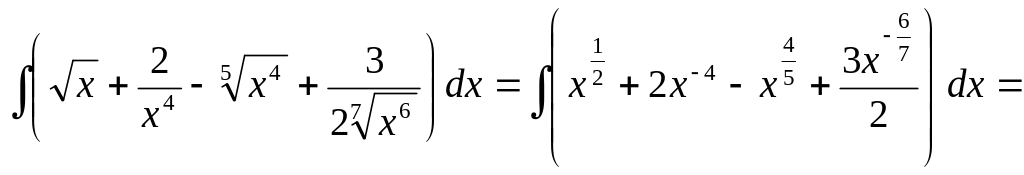
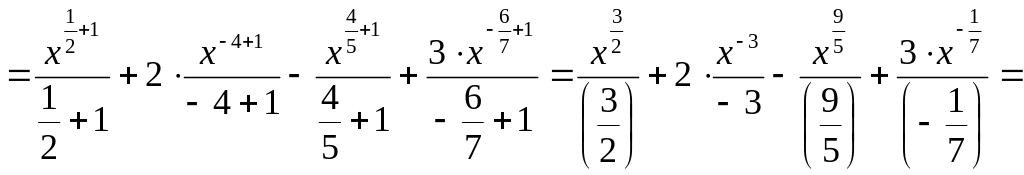
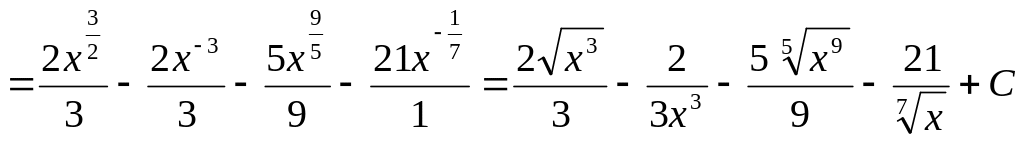
Пример.
Дифференциалом функции
называется
Например:
1)
2)
3)
Пример.
Пример.
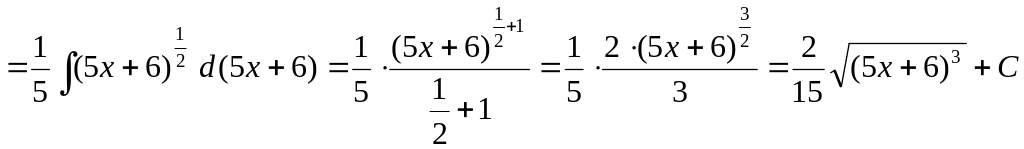
Пример.
Пример.
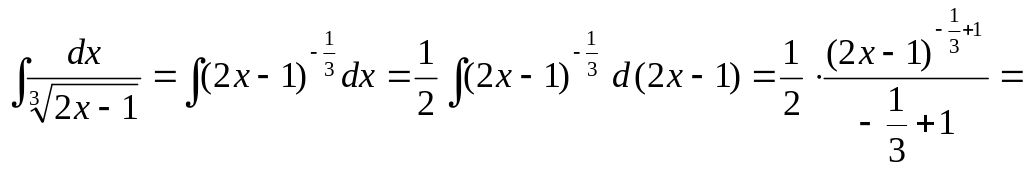
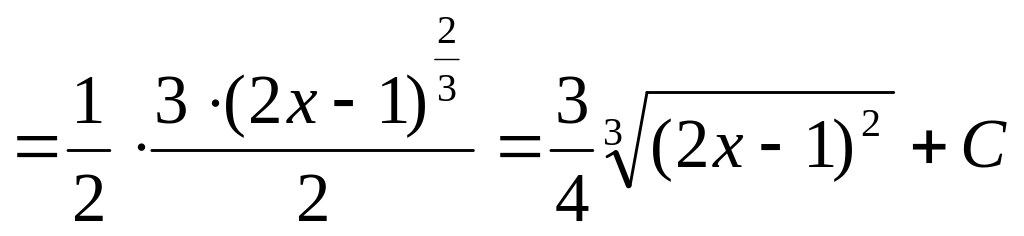
Выражение
называется полным квадратом.
Пример.
При нахождении интегралов иногда
используют формулу
Например:
Пример.
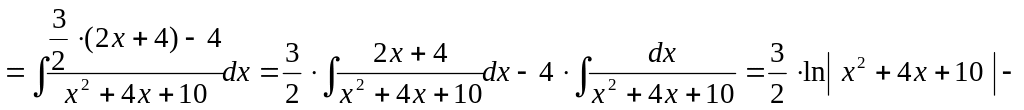
Задание 1.
1)
2)
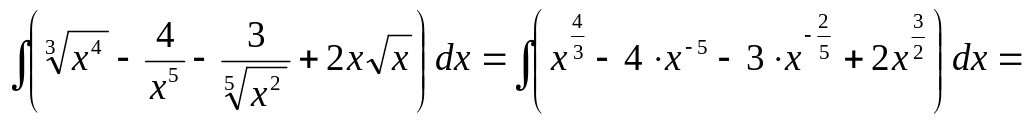
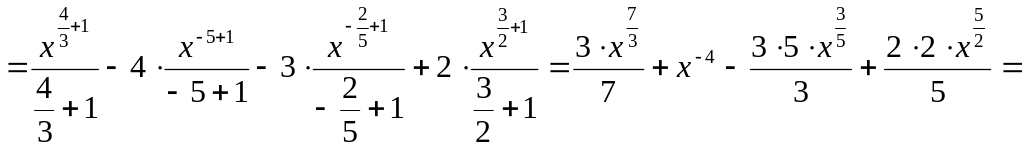
3)
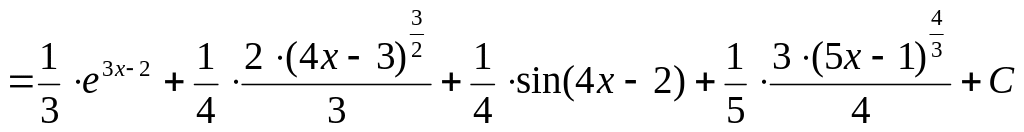
4)
5)
6)
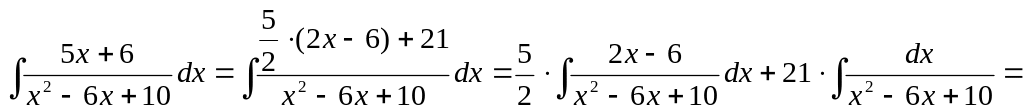
5.Определенный интеграл.
Определенный интеграл вычисляется по формуле Ньютона-Лейбница:
Здесь
и
называются пределами интегрирования,
- первообразная
,
то есть неопределенный интеграл. Для
вычисления определенного интеграла
надо найти первообразную, найти ее
значения на верхнем пределе, на нижнем
пределе и вычесть.
Пример.
1)
2)
С помощью определенного интеграла находятся площади фигур, длины кривых, объемы тел и т.д.
Площадь криволинейной трапеции находится по формуле:
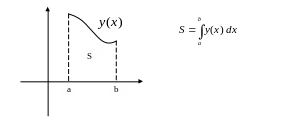
Пример.
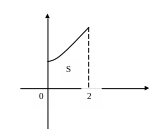
Найти площадь фигуры, ограниченной
кривыми
Строим параболу
,
прямую
,
- ось
,
- ось
.
В более общем случае площадь плоской
фигуры, ограниченной линиями
находится по формуле:
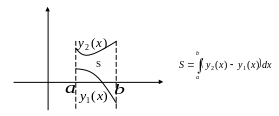
Пример. Найти площадь фигуры,
ограниченной кривыми
Строим параболу
.
Находим точки пересечения параболы с
осью
.
Прямую
строим по двум точкам:
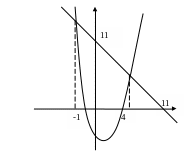
Находим точки пересечения параболы и прямой:
Находим площадь фигуры:
Задание 1. Найти определенный интеграл.
1)
2)
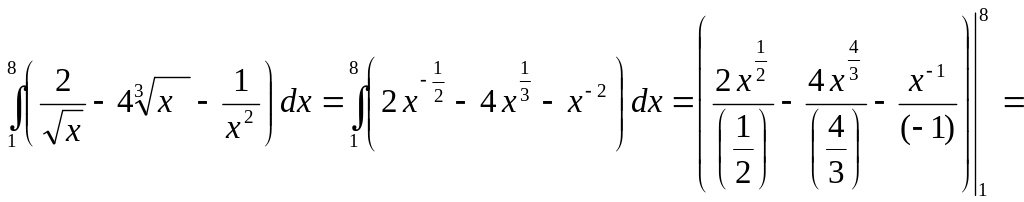
3)
4)
