Дифференциальное исчисление.
Односторонние пределы, непрерывность функции в точке. Точки разрыва функции и их классификация.
Таблица основных производных, правила дифференцирования. Производная сложной функции.
Пусть задана функция
.Обозначим
- малое приращение
.
Тогда производной
называется
Правила дифференцирования.
1). Производная от числа равна нулю:
2). Постоянный множитель можно выносить
за знак производной:
3) Производная суммы равна сумме производных:
4) Правило для произведения функций:
5) Правило для дроби:
Таблица производных.
1)
8)
2)
9)
3)
10)
4)
11)
5)
12)
6)
13)
7)
Найти производные функций.
Пример 1.
Пример 2.
Пример 3.
Напомним, что
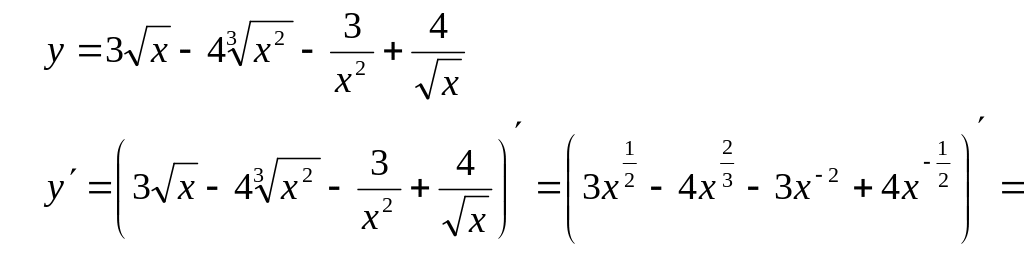
Пример 4.
Пример 5.
Пример 6.
Производная сложной функции.
Пусть
Запишем таблицу производных для сложной функции.
1)
8)
2)
9)
3)
10)
4)
11)
5)
12)
6)
13)
7)
Найти производные сложных функций.
Пример 1.
Пример 2.
Пример 3.
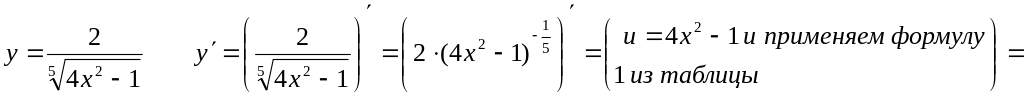
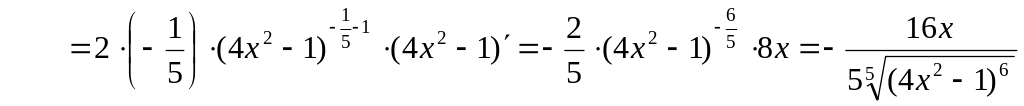
Пример 4.
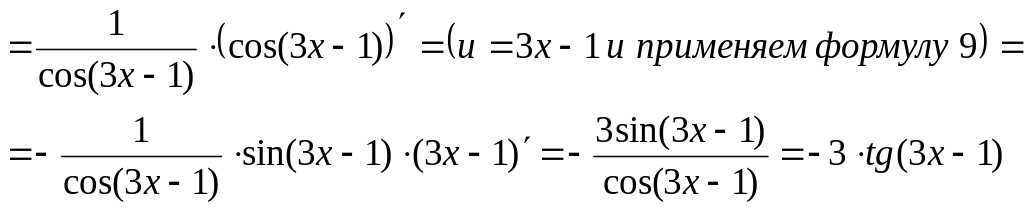
Пример 5.
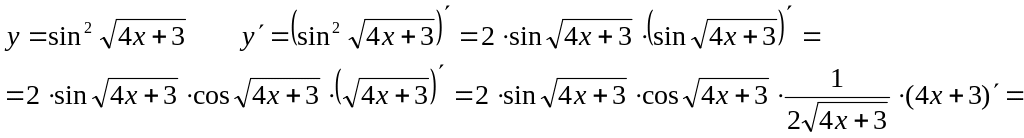
Пример 6.
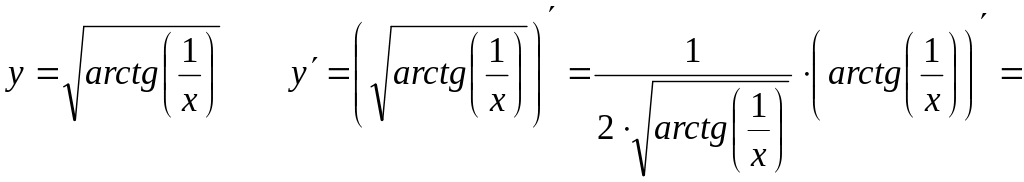
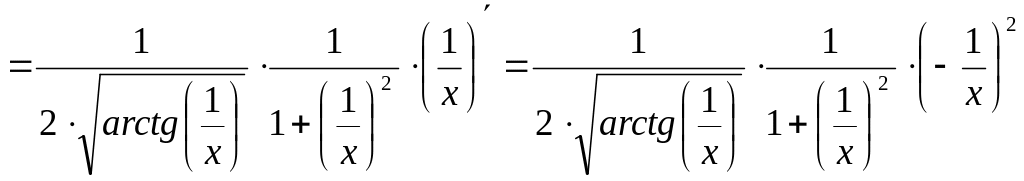
Задание 2. Вычислить производные функций.
1)
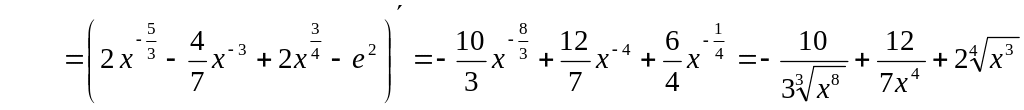
2)
3)
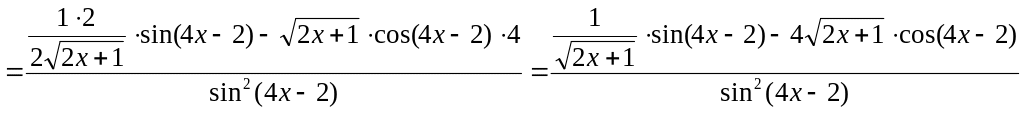
4)
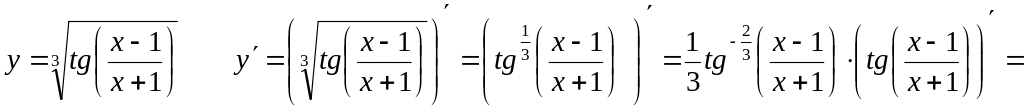
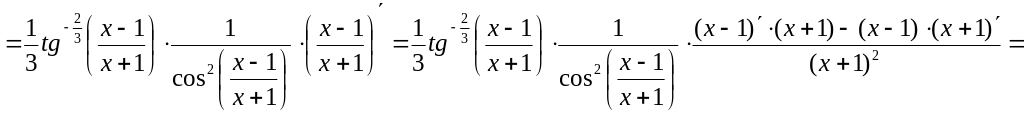
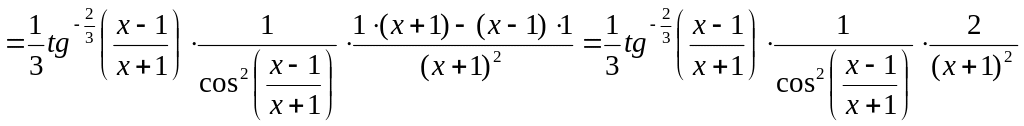
Интервалы монотонности, экстремум функции одной переменной. Выпуклость, вогнутость функции, точки перегиба.
При построении графика функции надо найти:
область определения
четность, нечетность
интервалы возрастания и убывания, экстремумы
интервалы выпуклости и вогнутости, точки перегиба
асимптоты
Экстремумы функции находятся по следующей схеме:
Находим производную, приравниваем к нулю, решаем это уравнение. Корни уравнения называются критическими точками. Корни знаменателя производной тоже называются критическими точками.
Критические точки отмечаем на прямой и на каждом интервале ставим знак
производной
Если
,
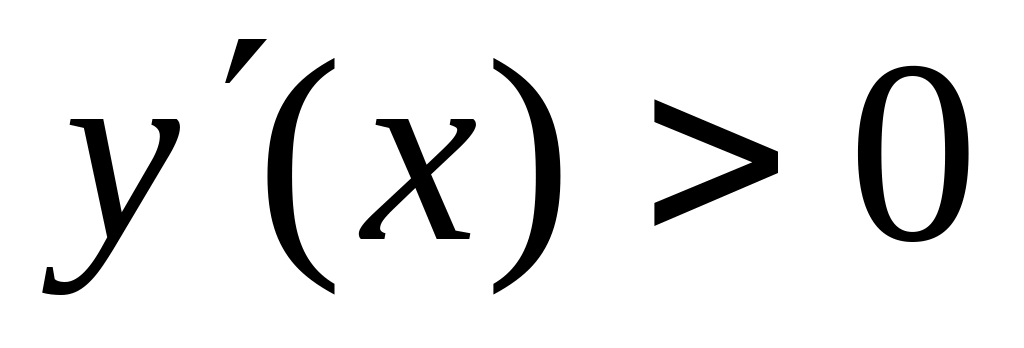на этом интервале функция возрастает,
если
,
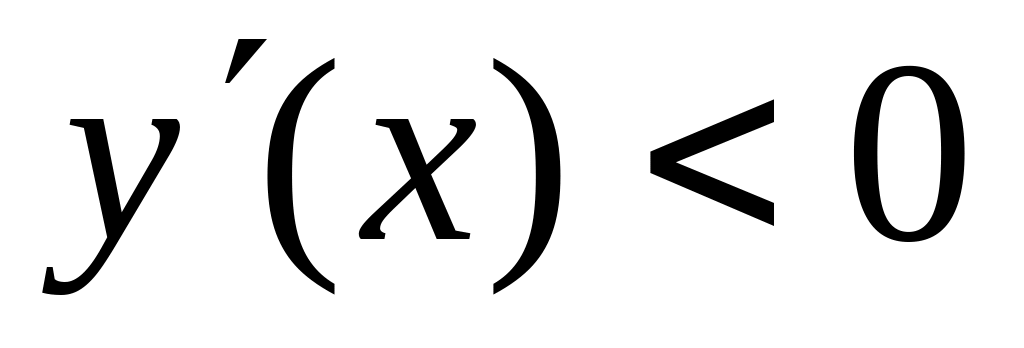на этом интервале функция убывает.Если при переходе через критическую точку производная меняет свой знак с «плюс» на «минус», то в точке - максимум. Если при переходе через критическую точку производная меняет свой знак с «минус» на «плюс», то в точке - минимум.
Пример. Найти экстремумы функции
Отмечаем точки на оси и ставим знаки производной.
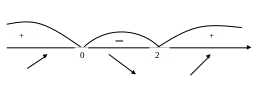
В точке
- максимум, в точке
- минимум. Подставляя
и
в функцию, найдем
.
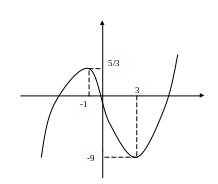
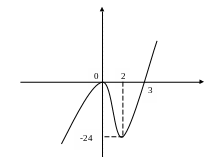
Пример. Построить график функции
Найдем точки пересечения графика с осью
.
Экстремумы найдены в предыдущем примере.
.
Пример. Построить график функции
Найдем экстремумы.
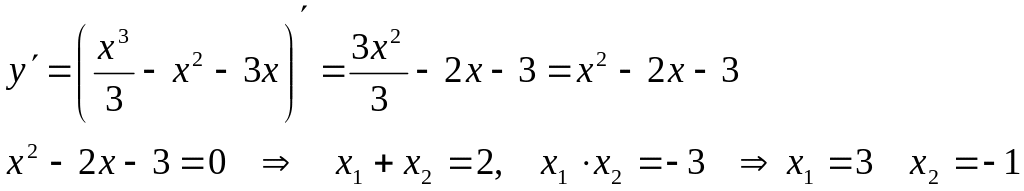
Отмечаем точки на прямой и на полученных интервалах ставим знаки производной.
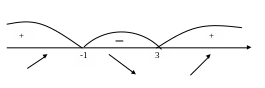
Строим график функции.
