Кривые второго порядка.
Эллипс.
Эта кривая задается уравнением
.
Это уравнение называется каноническим.
Чтобы сделать эскиз этой кривой, на оси
OX надо отметить точки
,
а на оси OY отметить точки
.
Эти точки соединить плавной линией.
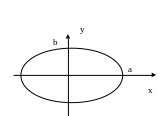
Если центр кривой смещается из начала координат в другую точку, уравнение кривой изменяется.
Пример. Выделяя полные квадраты, сделать эскиз эллипса.
Выделяем полные квадраты.
.
Приведем это уравнение к каноническому
виду.
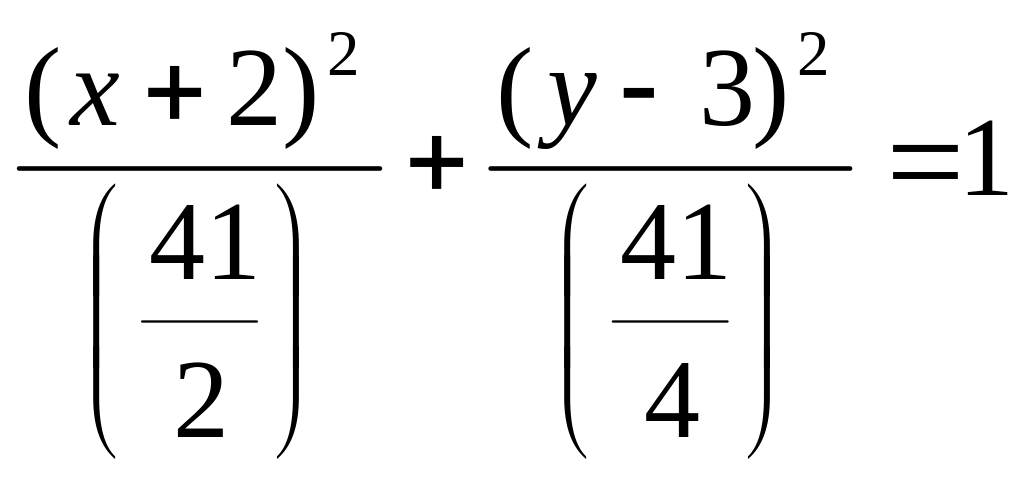Значит, центр эллипса находится в точке
,
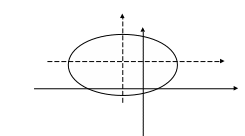
Чтобы сделать эскиз кривой, отмечаем центр эллипса, пунктирными линиями переносим в нее оси координат.
Гипербола.
Эта кривая задается уравнением
.
Это уравнение называется каноническим.
Чтобы сделать эскиз этой кривой, на оси
OX надо отметить точки
,
а на оси OY отметить точки
.
Построить прямоугольник, проходящий
через эти точки и пунктиром провести
прямые, проходящие через диагонали
этого прямоугольника. Эти прямые
называются асимптотами гиперболы. Затем
вписываются две ветви гиперболы.
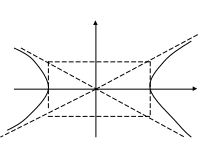
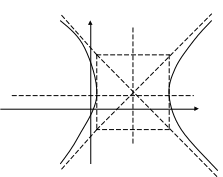
Пример. Выделяя полные квадраты, сделать эскиз гиперболы.
центр кривой в точке
.
Отмечаем центр гиперболы, пунктирными линиями переносим в нее оси координат, строим прямоугольник, проводим в нем диагонали и вписываем две ветви гиперболы.
Заметим, что если получилось уравнение
,
то надо поменять знак:
.
У этой гиперболы ветви направлены не
вправо и влево, а вверх и вниз. Строится
такая гипербола точно также, только
ветви гиперболы вписываются в верхний
и нижний угол между асимптотами.
Парабола.
Эта кривая задается уравнением
или
.
Эти уравнения называются каноническими.
Чтобы сделать эскиз параболы, надо найти
ее вершину и определить, в какую сторону
направлены ее ветви. Если в уравнении
в первой степени находится
,
то ветви вдоль оси
.
Если
,
ветви вправо, если
,
ветви влево. Если в уравнении в первой
степени находится
,
то ветви вдоль оси
.
Если
,
ветви вверх, если
,
ветви вниз.
Пример. Выделяя полные квадраты, сделать эскиз параболы.
1)
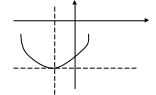
вершина параболы в точке
,
ветви вдоль оси
вверх.
2)
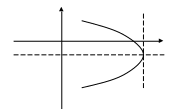
вершина параболы в точке
,
ветви вдоль оси
влево.
Введение в математический анализ.
Вычисление пределов последовательностей и функций.
Пусть задана функция
.
Если при неограниченном приближении
к
соответствующие значения функции
неограниченно близко приближаются к
числу А, то говорят, что функция
имеет предел и пишут
.
При вычислении предела надо в функцию
подставить
.
Пример. Вычислить предел функции.
1)
2)
Функция
называется бесконечно большой (б.б.),
если
.
Функция
называется бесконечно малой (б.м.), если
.
Пусть
,
тогда
и
Эти правила для краткости можно записать
следующим образом:
Пример. Вычислить предел функции.
1)
2)
При вычислении пределов после подстановки может получиться:
.
Эти выражения называются неопределенностью.
Для каждого вида неопределенности
существует свой способ «раскрытия».
Неопределенность вида
.
Для раскрытия этой неопределенности достаточно сравнить степени числителя и знаменателя по простому правилу:
Пример. Вычислить предел функции.
1)
2)
3)
4)
Неопределенность вида
.
Для раскрытия этой неопределенности надо сократить дробь.
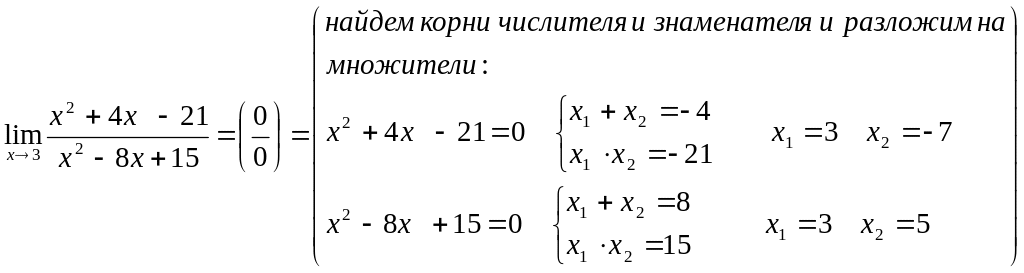
В некоторых случаях надо использовать таблицу эквивалентностей.
Две бесконечно малые величины
и
называются
эквивалентными, если
.
Обозначение
Приведем основные эквивалентности.
При
верно:
1)
2)
3)
4)
5)
6)
7)
Пример. Вычислить предел функции.
1)
2)
3)
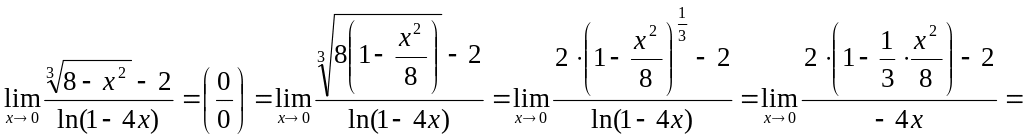
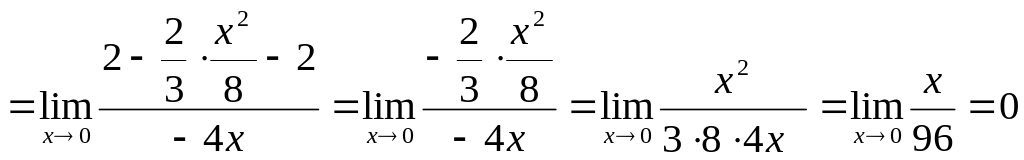
Неопределенность вида
.
Для раскрытия этой неопределенности надо преобразовать выражение так, чтобы получилась неопределенность вида . Например, привести к общему знаменателю.
Пример. Вычислить предел функции.
Неопределенность вида
.
Для раскрытия этой неопределенности применяется второй замечательный предел:
Пример. Вычислить предел функции.
1)
2)
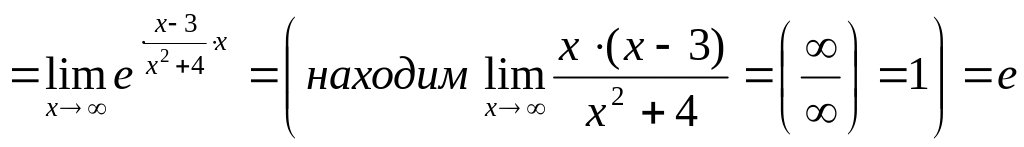
3)
Задание 1. Вычислить пределы функций.
1)
2)
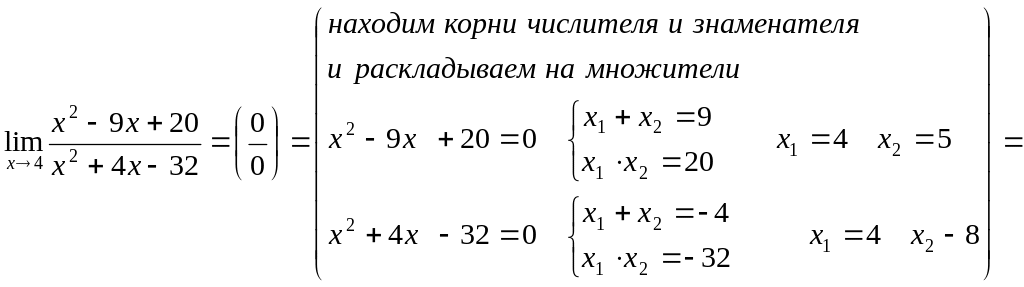
3)
Задание 2. Вычислить предел функции.
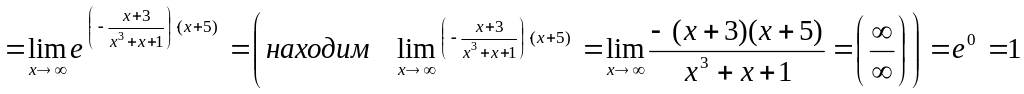
Задание 3. Вычислить пределы, используя эквивалентные бесконечно малые.
1)
2)
