1. Прямая на плоскости.

Всякая прямая задается линейным уравнением вида . Это уравнение называется общим уравнением прямой. Если из этого уравнения выразить , то получится вид с угловым коэффициентом, а именно . Здесь называется угловым коэффициентом и равен тангенсу угла наклона прямой к оси , то есть .

Пример.

Под каким углом пересекают данные прямые ось .

1)

2)

3)

Чтобы определить угловой коэффициент, надо из уравнения выразить :

4)

Запишем основные формулы.

1. Уравнение прямой с заданным угловым коэффициентом , проходящей через точку .

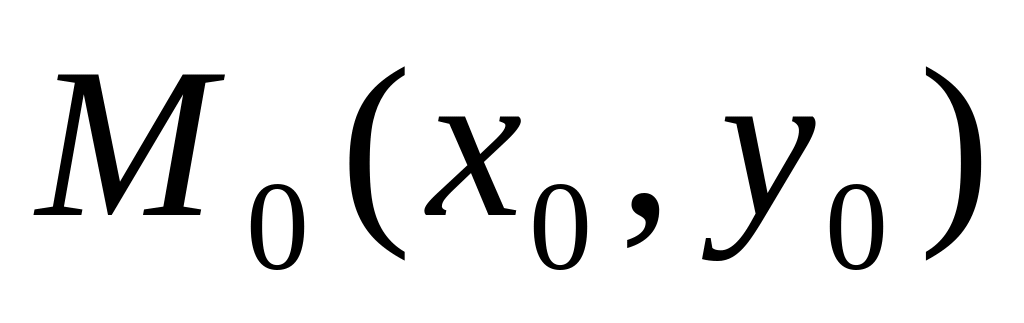2. Уравнение прямой, проходящей через точку 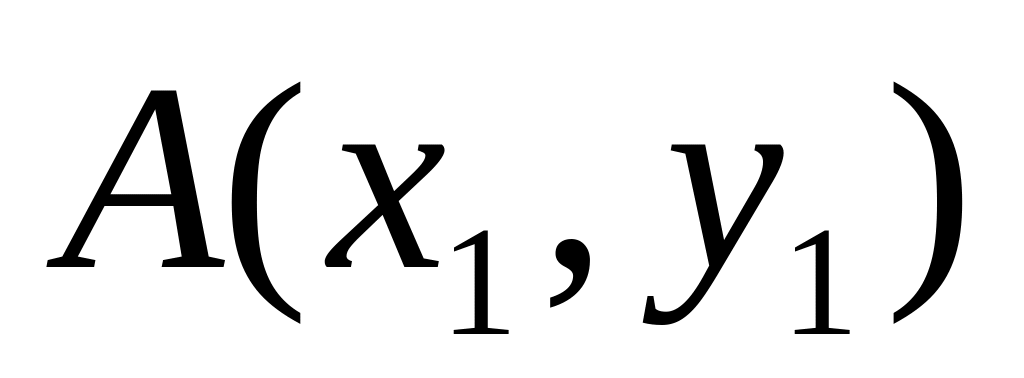и точку .

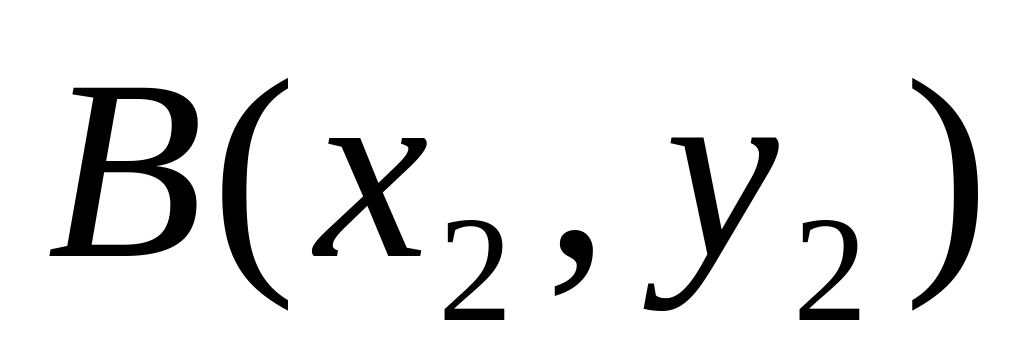3. Угол между прямыми 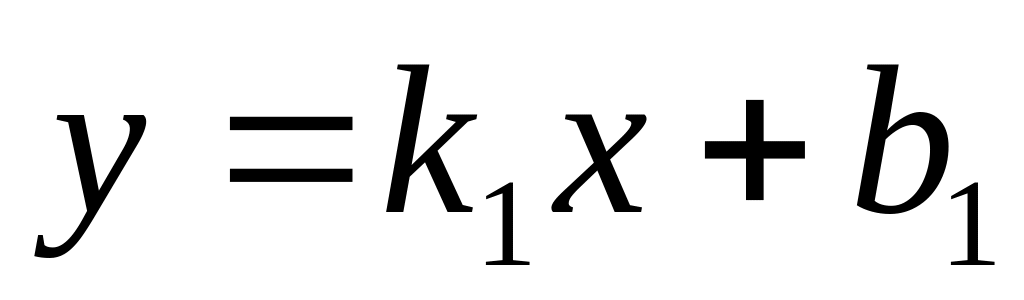и .

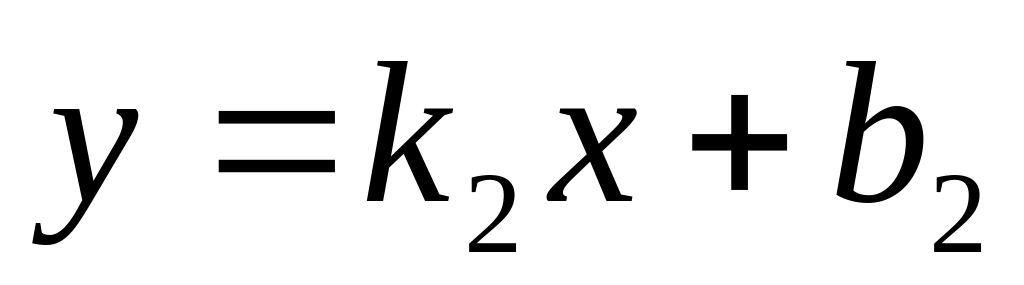4. Условия параллельности и перпендикулярности двух прямых 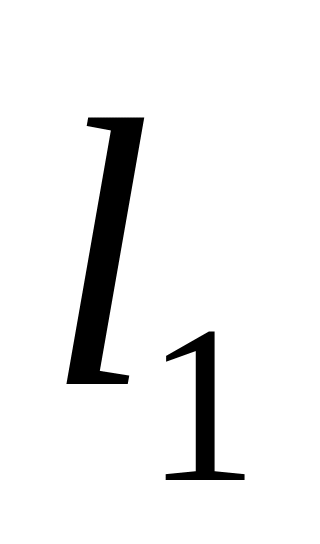и .

//

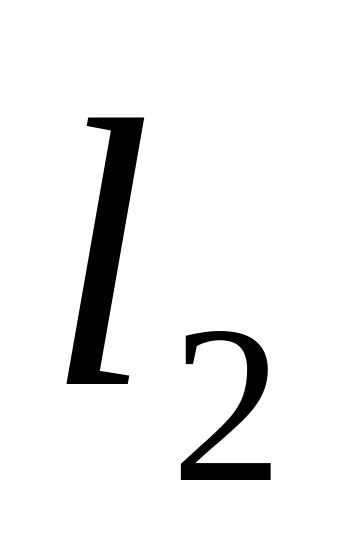5. Расстояние от точки до прямой .

Пример.

Составить уравнение прямой, проходящей через точку и точку .

Согласно уравнению 2:

Пример.

Составить уравнение прямой, проходящей через точку и точку .

Пример. Даны прямые и . Найти угол между этими прямыми.

Найдем угловые коэффициенты этих прямых: и

По формуле 3 находим тангенс угла между прямыми:

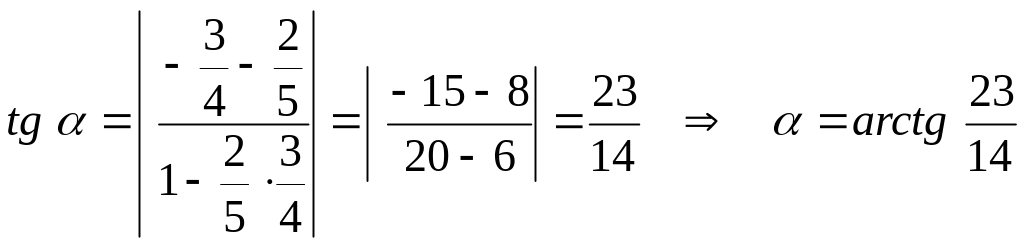
Пример. Составить уравнение прямой, проходящей через точку параллельно прямой .

Угловой коэффициент данной прямой , значит угловой коэффициент прямой, ей параллельной, . Используя уравнение 1, получим

Пример. Составить уравнение прямой, проходящей через точку перпендикулярно прямой .

Угловой коэффициент данной прямой , значит угловой коэффициент прямой, ей параллельной, . Используя уравнение 1, получим

Задание 1. В треугольнике с вершинами составить:

1. уравнения всех его сторон

2. уравнения всех высот

3. медианы

4. найти угол между медианой и высотой

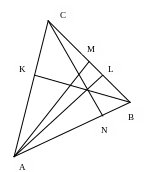
1) Составим уравнение стороны Используем уравнение

Составим уравнение стороны

Составим уравнение стороны

2) Составим уравнение высоты Угловой коэффициент прямой , значит,

угловой коэффициент перпендикулярной прямой .

Используем уравнение

Составим уравнение высоты AL. Угловой коэффициент прямой , значит,

угловой коэффициент перпендикулярной прямой .

Составим уравнение высоты . Угловой коэффициент прямой , значит,

угловой коэффициент перпендикулярной прямой .

3)Составим уравнение медианы Точка М – середина отрезка, а координаты середины отрезка есть полусумма координат концов отрезка. Значит, или .

Используем формулу

4) Найдем угол между медианой и высотой . Угловой коэффициент прямой , угловой коэффициент прямой .