2. Скалярное произведение векторов.

Скалярным произведением векторов и называется число

.

Здесь - угол между этими векторами, - длины векторов.

Скалярное произведение позволяет:

1. Находить угол между векторами по формуле

2. Находить проекцию вектора на вектор по формуле

3. Проверять, будут ли векторы перпендикулярны, так как

Пусть в ортонормированном базисе заданы векторы и .

Тогда длина (модуль) вектора находится по формуле , а скалярное произведение

Пример.

Найти расстояние между точкой и точкой .

Запишем координаты вектора : , значит,

Находим длину этого вектора:

Пример.

Проверить, будут ли векторы и перпендикулярны.

Для проверки перпендикулярности надо найти скалярное произведение.

Значит,

Задание 2. В треугольнике АВС найти периметр, косинус угла при вершине В и проекцию

вектора на вектор .

Треугольник задан вершинами

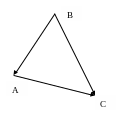
Найдем координаты векторов , и :

, . Тогда ,

, .

Значит, периметр треугольника равен .

Найдем угол при вершине В:

Найдем проекцию:

3.Векторное произведение векторов.

Векторным произведением векторов и называется вектор , определяемый следующим образом:

1)

2)

3) векторы образуют правую тройку.

С помощью векторного произведения можно находить:

1) Вектор, перпендикулярный плоскости, которой параллельны векторы и

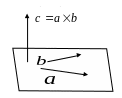
2) Площадь параллелограмма и треугольника, построенного на векторах и соответст-

венно по формулам:

Вычисляется векторное произведение с помощью определителя:

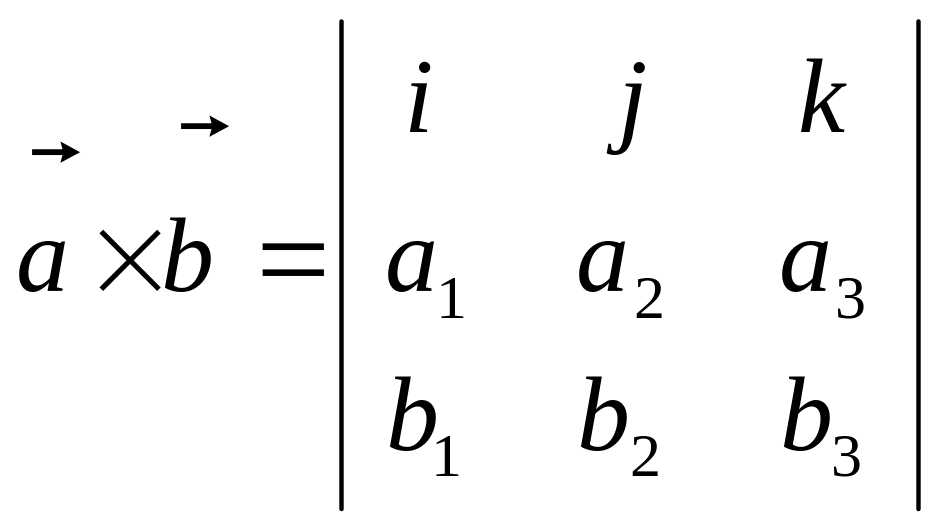
Пример. Найти векторное произведение векторов и

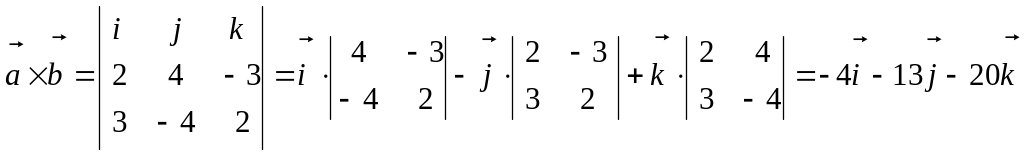
Проверим вычисления. Так как и , то надо убедиться, что скалярные произведения равны нулю:

Пример. Найти площадь треугольника с вершинами

Найдем координаты векторов , : . Затем находим векторное произведение:

.

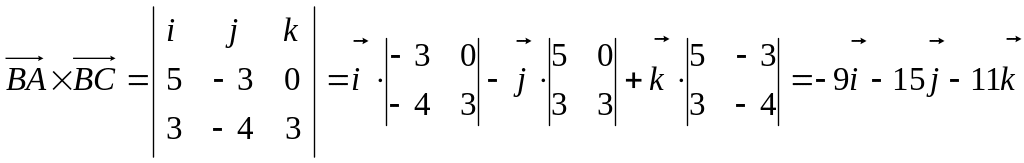
Задание 3.

1. Найти вектор , перпендикулярный вектору 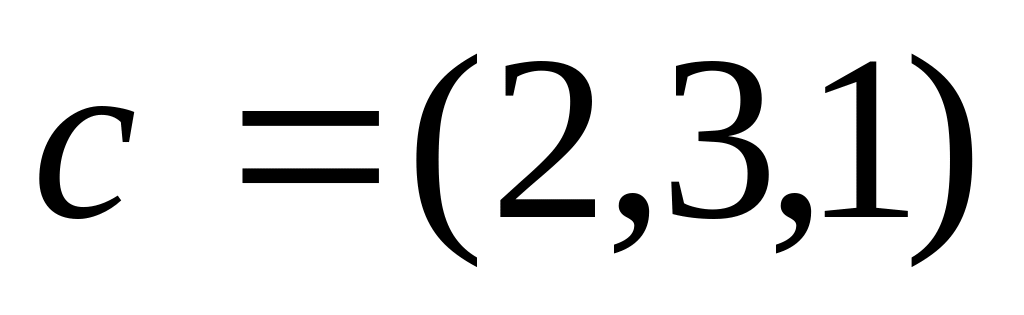и вектору .

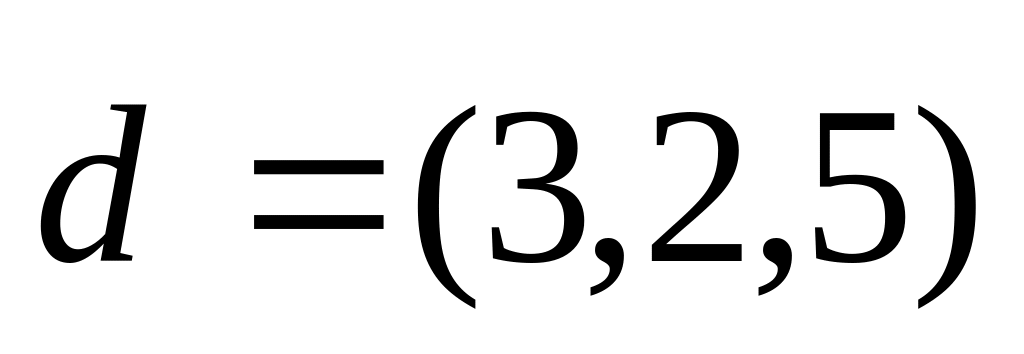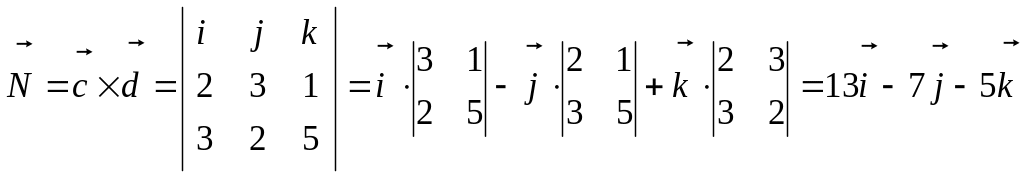
Ответ:

2. Найти площадь треугольника с вершинами .

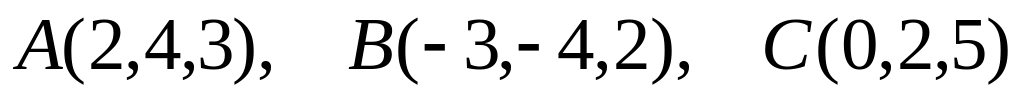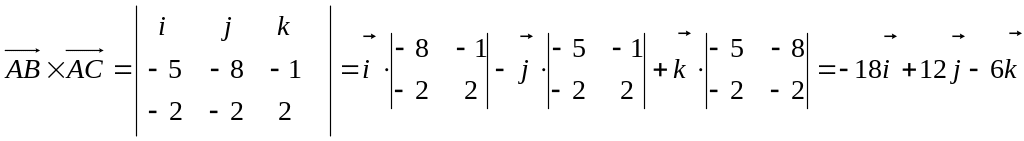
Ответ:

5.Смешанное произведение векторов.

Смешанным произведением векторов называется число

Вычисляется смешанное произведение векторов по формуле

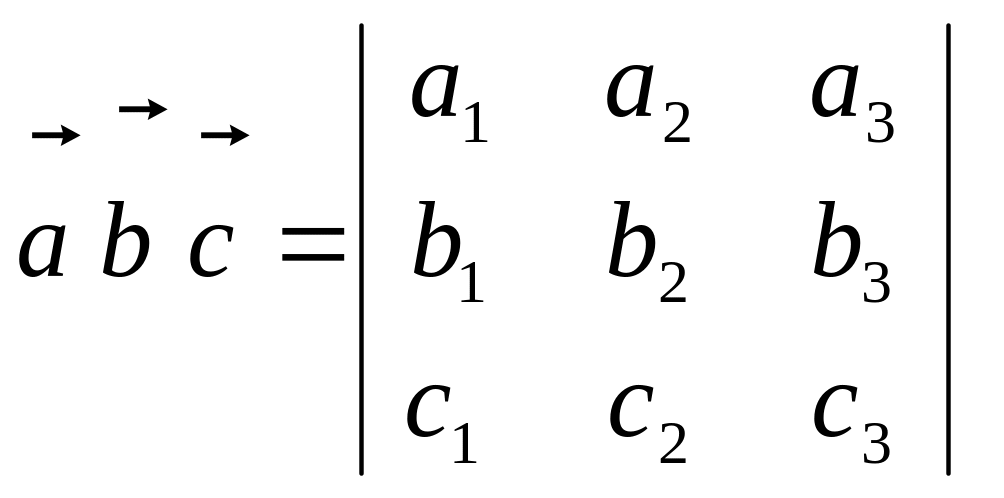
С помощью смешанного произведения можно находить:

1) Объем параллелепипеда, построенного на векторах :

2) Объем тетраэдра, построенного на векторах :

Пример. Найти объем тетраэдра с вершинами

Находим смешанное произведение векторов

на которых построен этот тетраэдр.

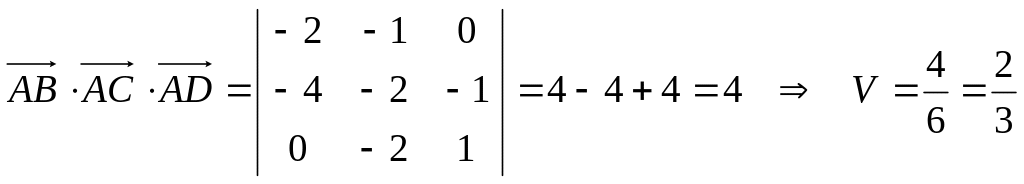
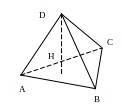
Задание 5. Найти объем тетраэдра ABCD с вершинами и найти длину его высоты, проведенной из вершины D.

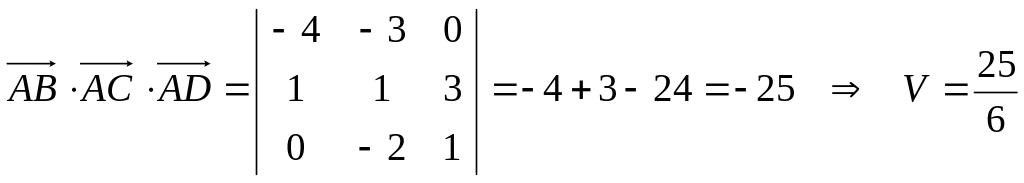
С другой стороны объем пирамиды можно найти по формуле . Выразим отсюда искомую высоту: . Объем уже известен, а площадь треугольника ABC найдем с помощью векторного произведения векторов .

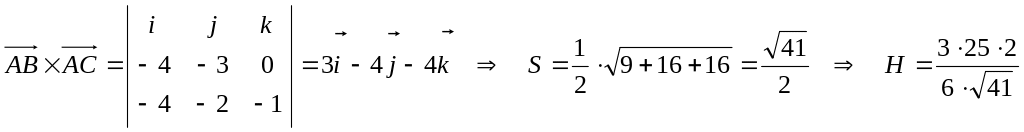
Ответ:

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.