2. Решение систем линейных алгебраических уравнений методом Крамера.

Покажем решение системы линейных алгебраических уравнений методом Крамера.

Задание 2. Решить систему уравнений.

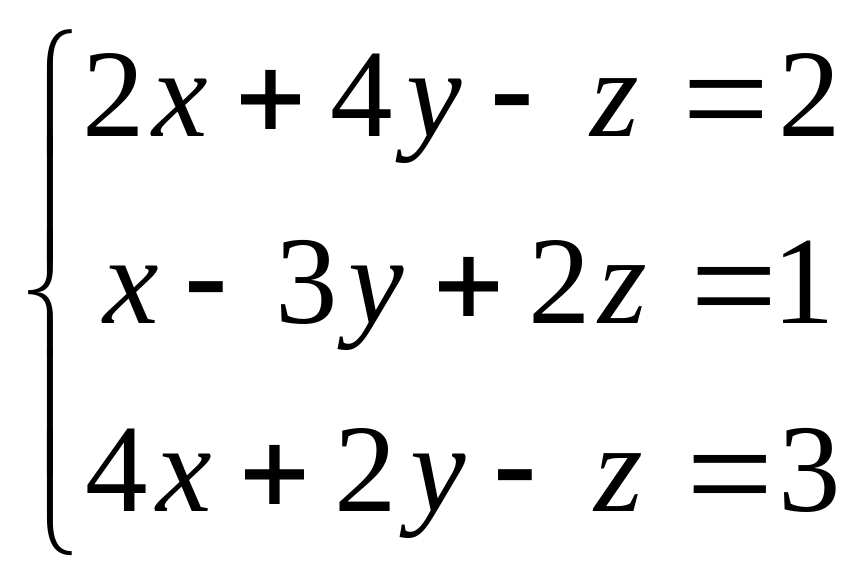
Надо вычислить четыре определителя. Первый называется основным и состоит из коэффициентов при неизвестных:

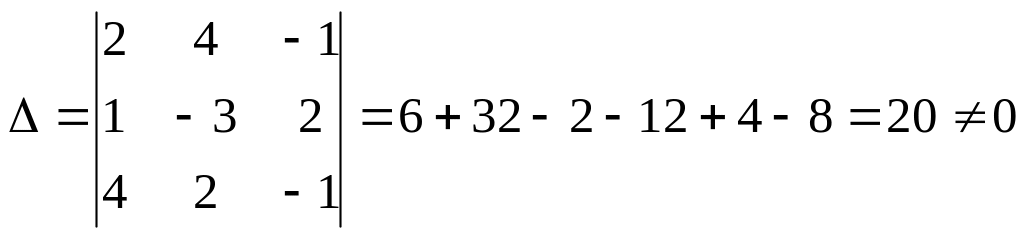
Заметим, что если , систему методом Крамера решить нельзя.

Три остальных определителя обозначаются , , и получаются заменой соответствующего столбца на столбец правых частей.

Находим . Для этого первый столбец в основном определителе меняем на столбец правых частей:

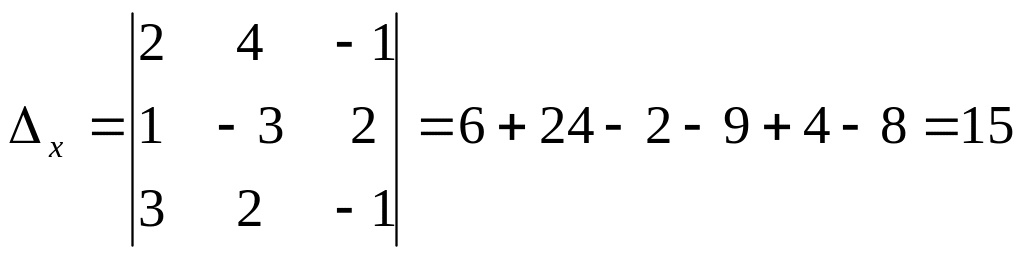
Находим . Для этого второй столбец в основном определителе меняем на столбец правых частей:

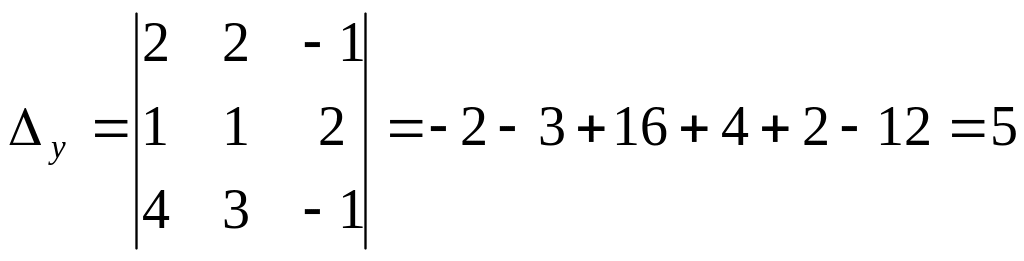
Находим . Для этого третий столбец в основном определителе меняем на столбец правых частей:

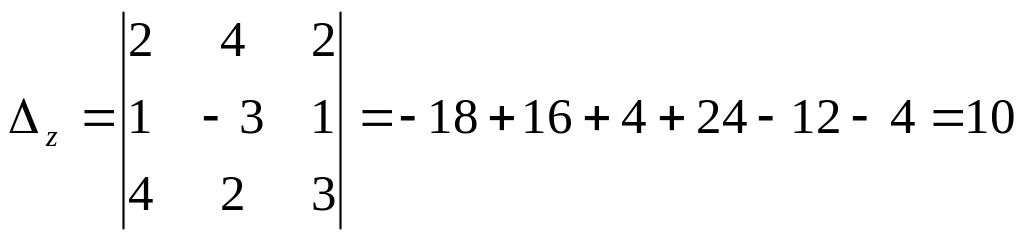
Решение системы находим по формулам Крамера: , ,

, ,

Таким образом решение системы , ,

Сделаем проверку, для этого найденное решение подставим во все уравнения системы.

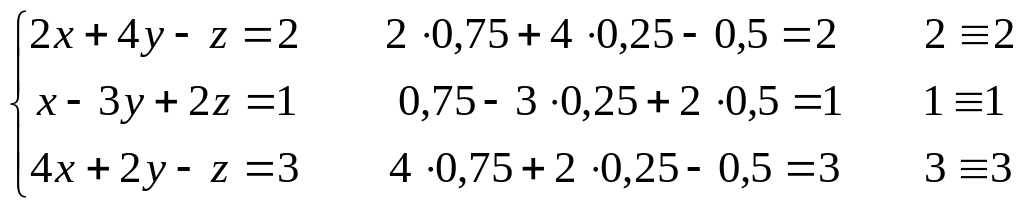
3. Решение систем линейных алгебраических уравнений матричным методом.

Если у квадратной матрицы определитель не равен нулю, существует обратная матрица , такая что . Матрица называется единичной и имеет вид

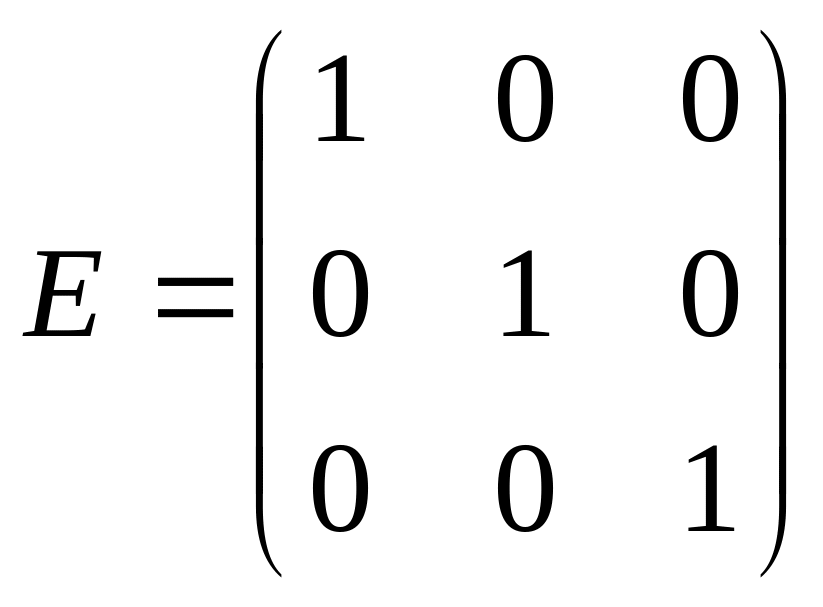
Обратная матрица находится по формуле:

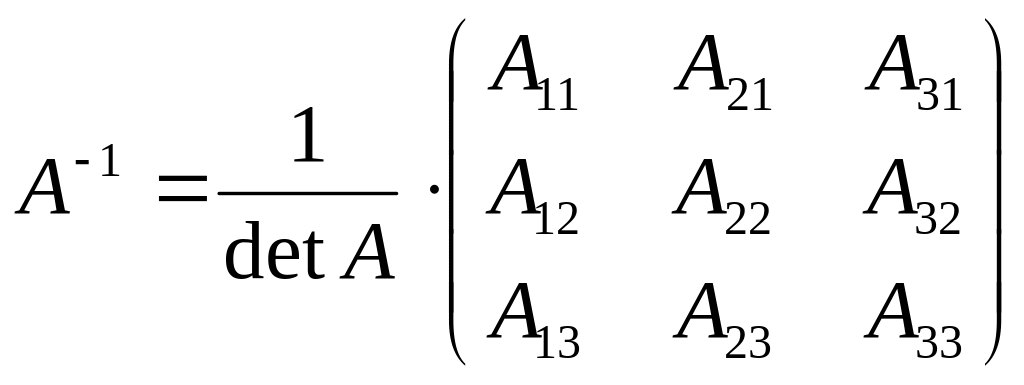
Пример. Найти обратную матрицу к матрице

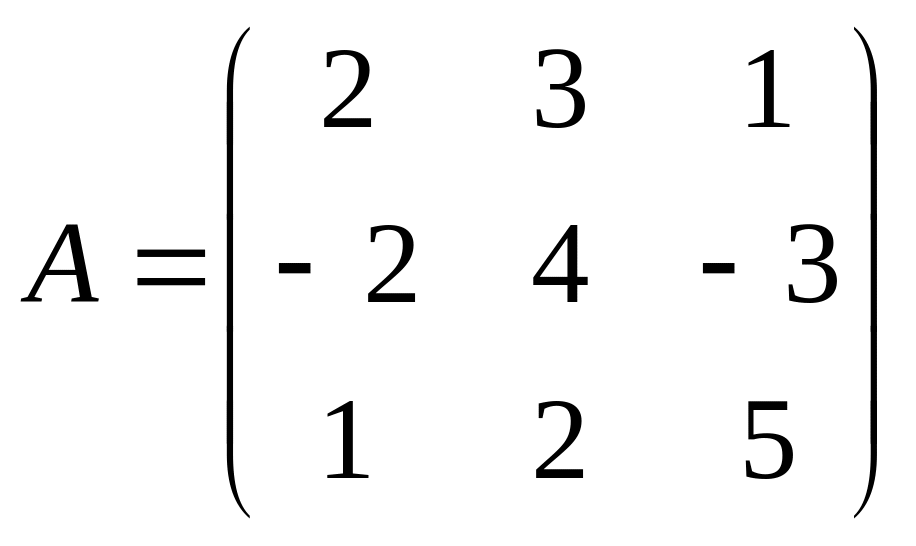
Сначала вычисляем определитель.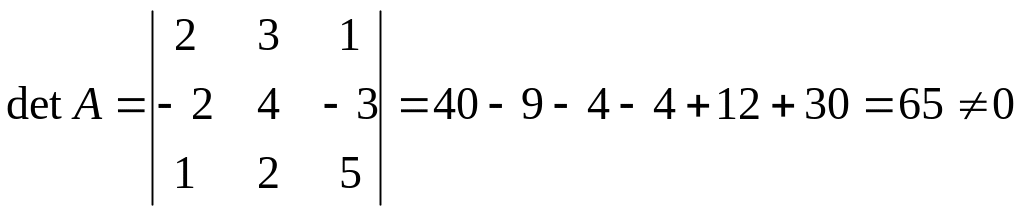

Находим алгебраические дополнения:

Записываем обратную матрицу:

Чтобы проверить вычисления, надо убедиться, что .

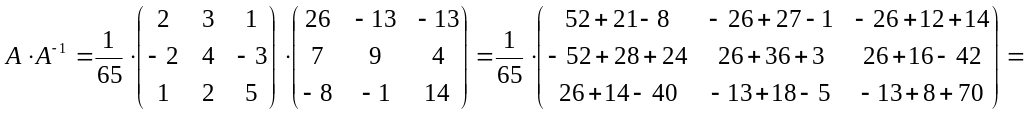
Пусть дана система линейных уравнений:

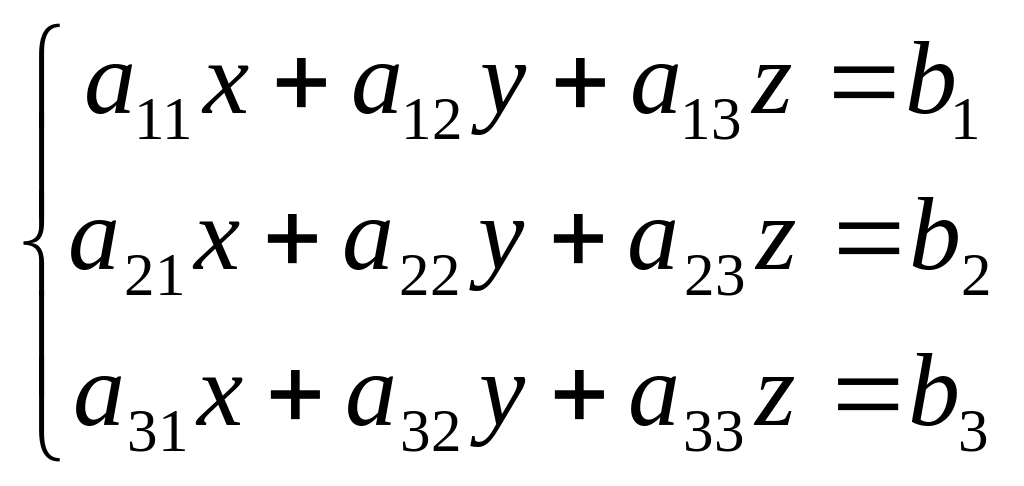
Обозначим

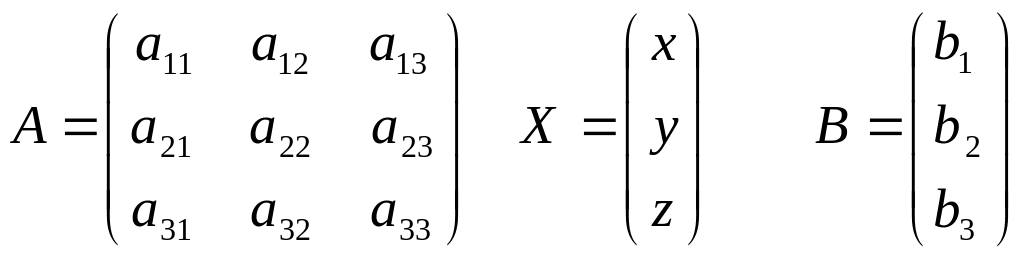
Тогда система уравнений может быть записана в матричной форме как , а отсюда . Полученная формула называется матричным способом решения системы.

Задание 3. Решить систему матричным способом.

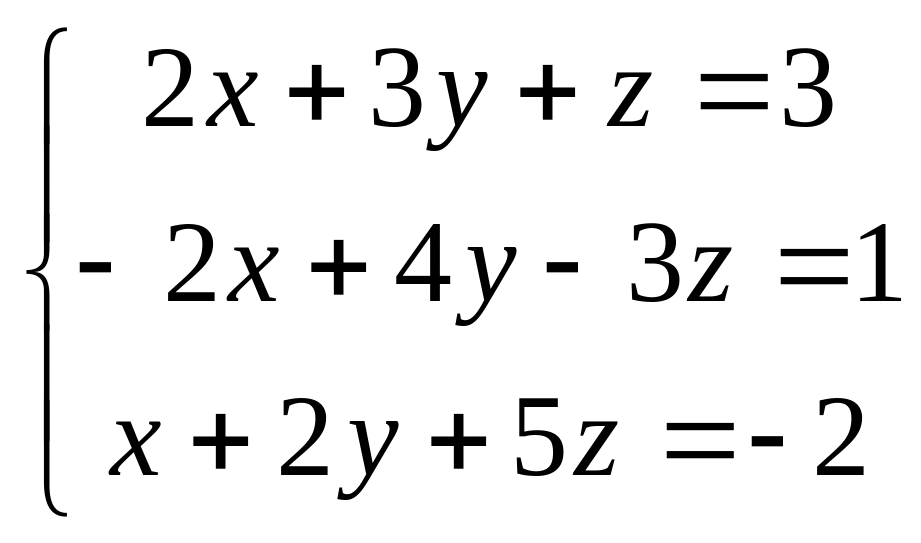
Надо выписать матрицу системы, найти к ней обратную и затем умножить на столбец правых частей.

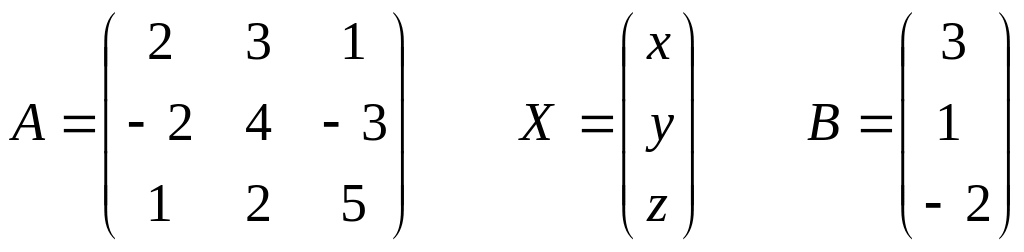
Обратная матрица у нас уже найдена в предыдущем примере, значит можно находить решение:

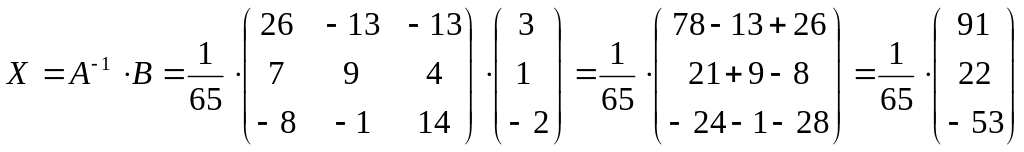
Ответ:

4. Решение систем линейных алгебраических уравнений методом Гаусса.

Метод Крамера и матричный метод применяется только для квадратных систем (число уравнений равно числу неизвестных), причем определитель должен быть не равен нулю. Если число уравнений не равно числу неизвестных, или определитель системы равен нулю, применяется метод Гаусса. Метод Гаусса можно применять для решения любых систем.

Мы рассмотрим решение системы четвертого порядка. Если применять метод Крамера, придется находить пять определителей четвертого порядка. Если решиться обращать матрицу четвертого порядка, то придется находить 16 определителей третьего порядка.

Метод Гаусса состоит в приведении матрицы системы к треугольной или трапециевидной форме.

Пример. Решить систему третьего порядка методом Гаусса.

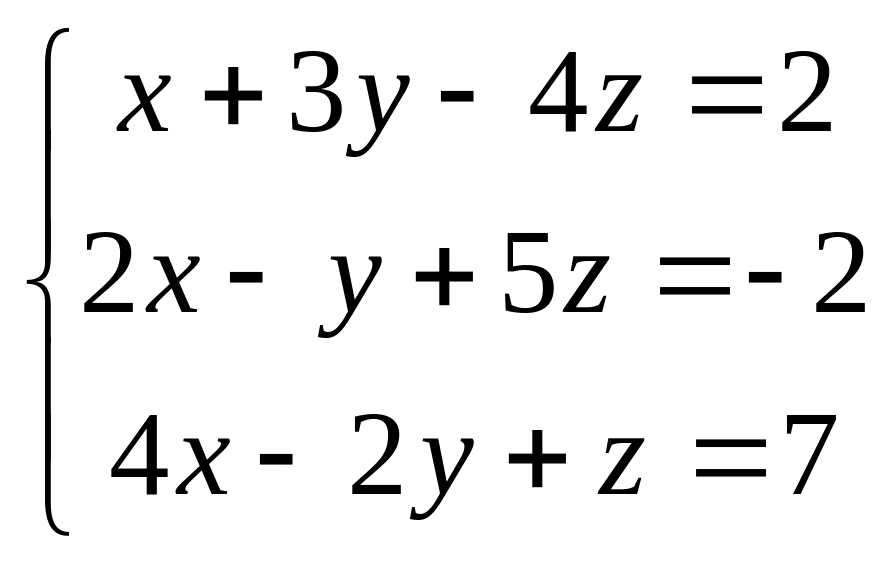
Выписываем матрицу системы, в которую включаем и правые части:

Матрица приведена к треугольной форме (столбец правых частей не считается). По матрице восстановим систему:

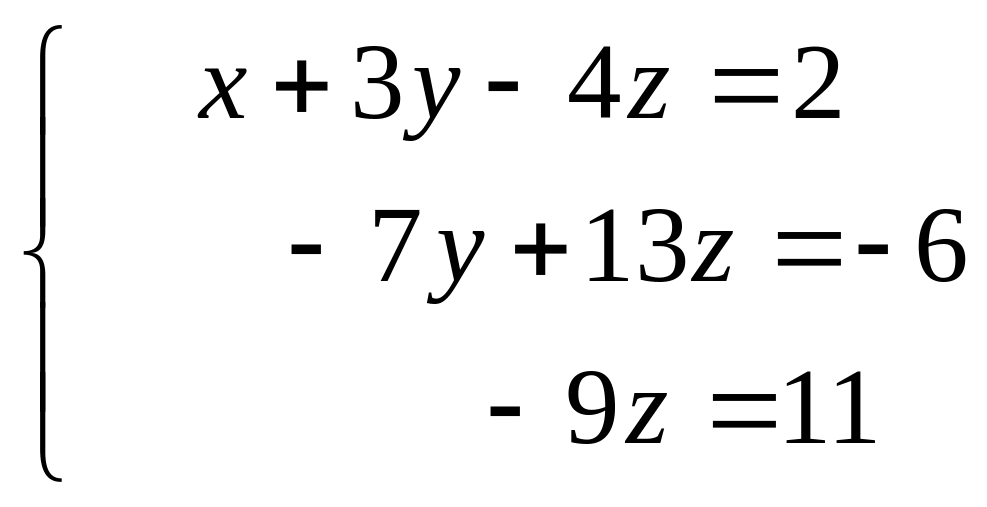
Из последнего уравнения находим . Подставим во второе уравнение:

. Найденные и подставим в первое уравнение:

Ответ:

Задание 5. Решить систему уравнений методом Гаусса.

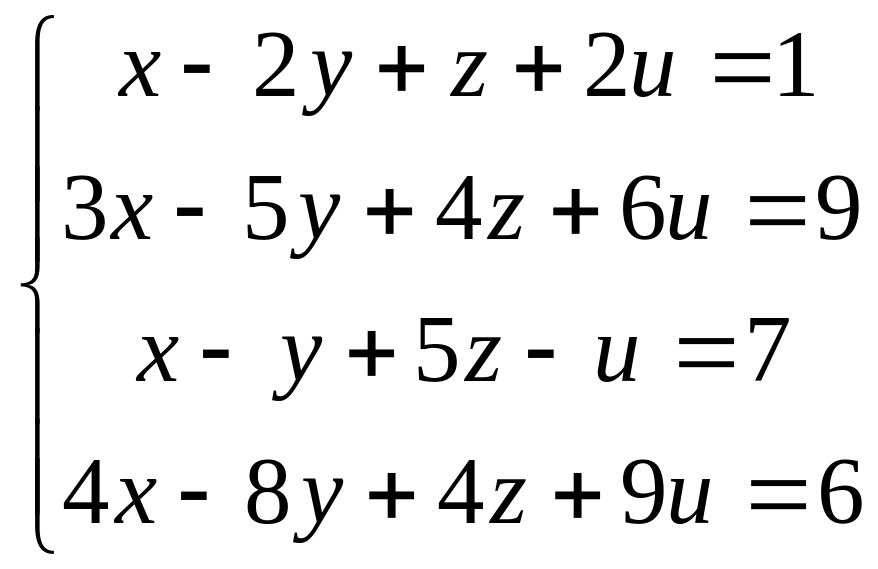
По полученной матрице восстанавливаем систему:

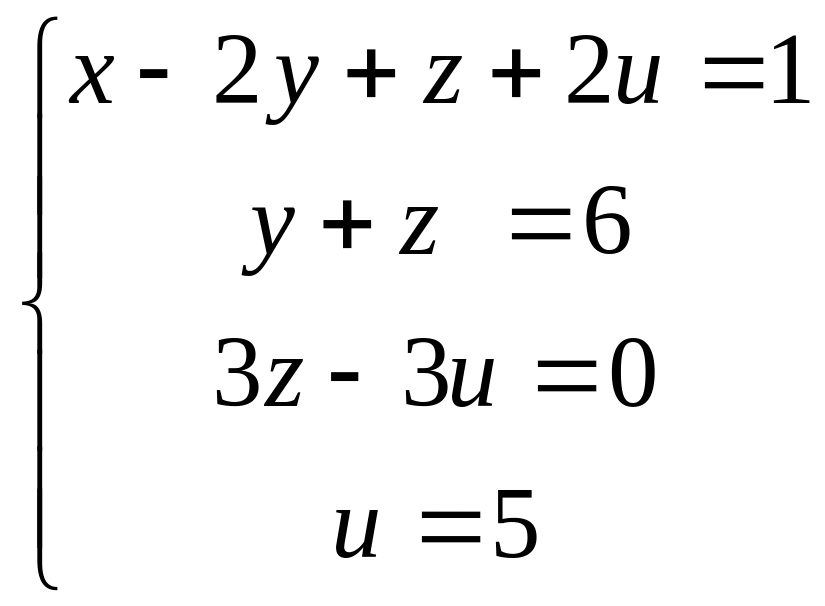
Находим решение:

Ответ:

ВЕКТОРНАЯ АЛГЕБРА.

1.

Рассмотрим прямоугольную декартову систему координат на плоскости. Единичный вектор оси обозначим , единичный вектор оси обозначим . Таким образом, и . Говорят, что векторы образуют ортонормированный базис на плоскости.

Любой вектор можно выразить через вектора , то есть представить в виде . Это представление называется разложением вектора по базису . Числа называются координатами вектора в базисе .

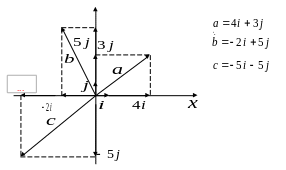
Любые два непараллельных вектора и образуют базис на плоскости и любой третий вектор может быть разложен по этому базису, то есть представлен в виде .Числа называются координатами вектора в базисе .

Пример. Проверить, что векторы и образуют базис и разложить вектор по этому базису.

Векторы параллельны, если их координаты пропорциональны:

координаты не пропорциональны, значит, векторы и непараллельны, то есть образуют базис.

Найдем числа такие, что .

Векторы слева и справа равны, значит, равны их координаты: