ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.

1. Действия над матрицами.

Матрицей называется прямоугольная таблица элементов, например

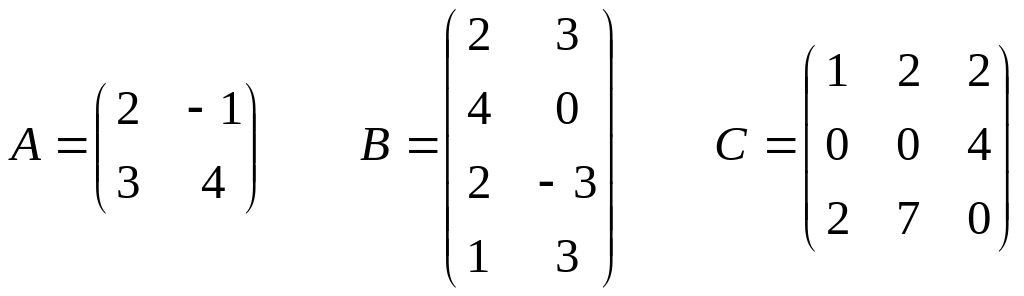
Размерность матрицы обозначают , где - число строк, а - число столбцов матрицы. Например, размерность матрицы А - , матрицы В - ,

матрицы - . В общем случае элемент матрицы обозначают , где - номер строки, а - номер столбца матрицы, на пересечении которых находится этот элемент. Например, для матрицы А , для матрицы В .

Определим действия над матрицами.

Умножение матрицы на число и сложение покажем на примерах.

1.Умножение матрицы на число.

Пример.

или

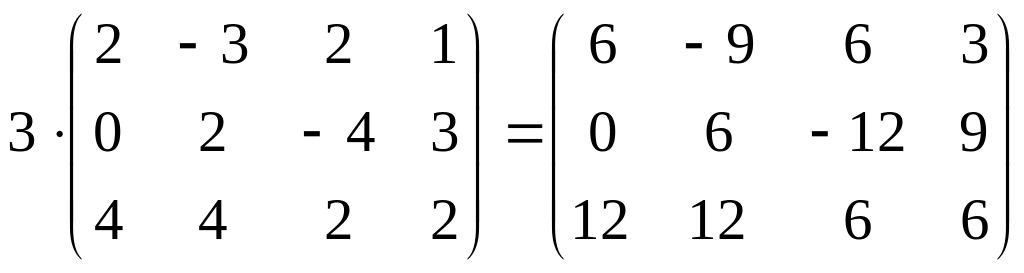
2.Сложение (вычитание) матриц.

Пример.

3.Умножение матриц.

Если матрица А имеет размерность , а матрица В имеет размерность , то их можно умножать. В результате получается матрица , размерность которой будет . Например, размерности , В размерности , то будет размерности .

Пример.

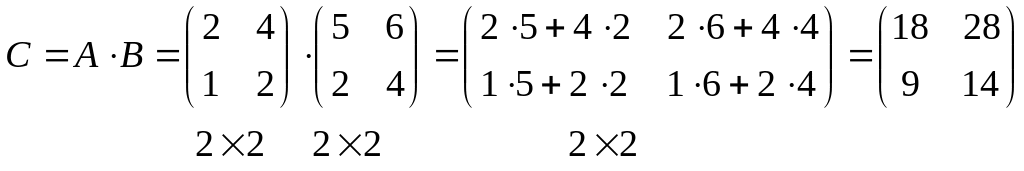
Первую строку А умножаем на первый столбец В: .

Первую строку А умножаем на второй столбец В: .

Вторую строку А умножаем на первый столбец В: .

Вторую строку А умножаем на второй столбец В: .

Пример.

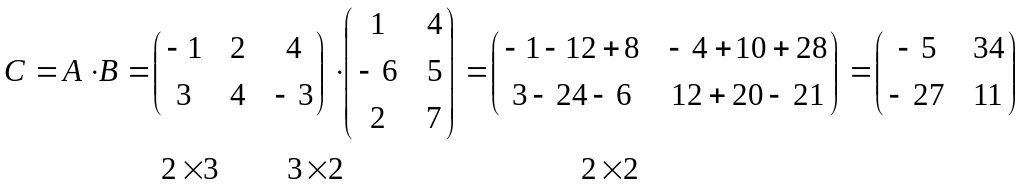
Пример.

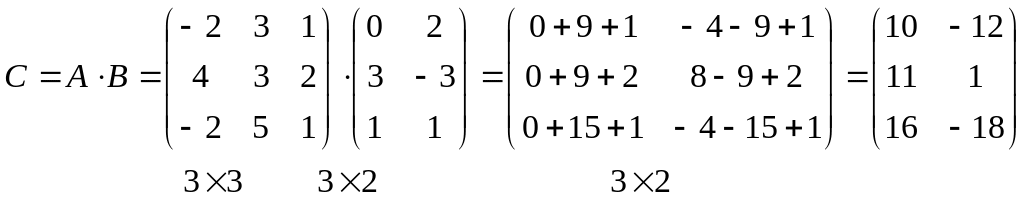
4. Транспонирование матриц.

Чтобы транспонировать матрицу, надо строки матрицы записать в столбцы.

Пример.

Если , то транспонированная матрица

Если , то

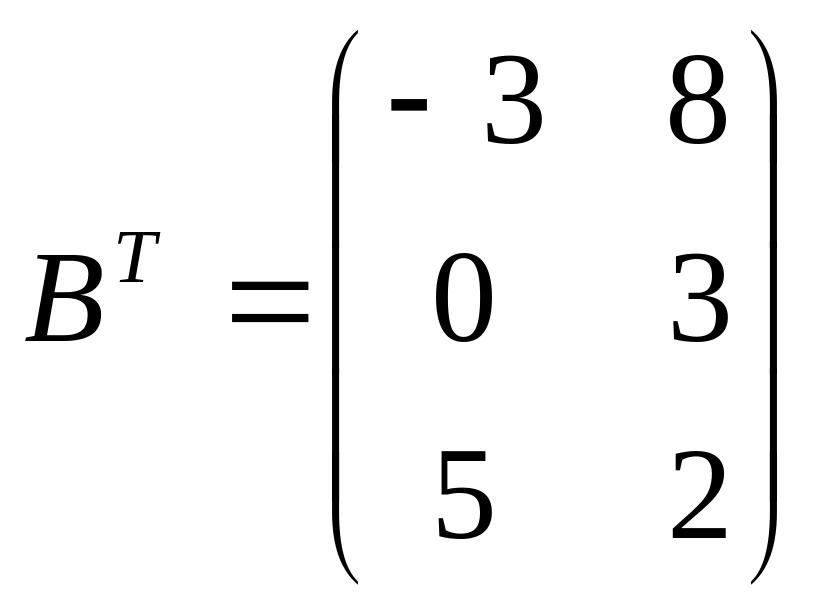
Задание 1. Найти

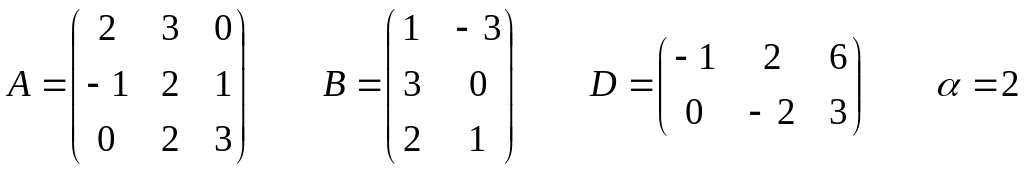
Решение.

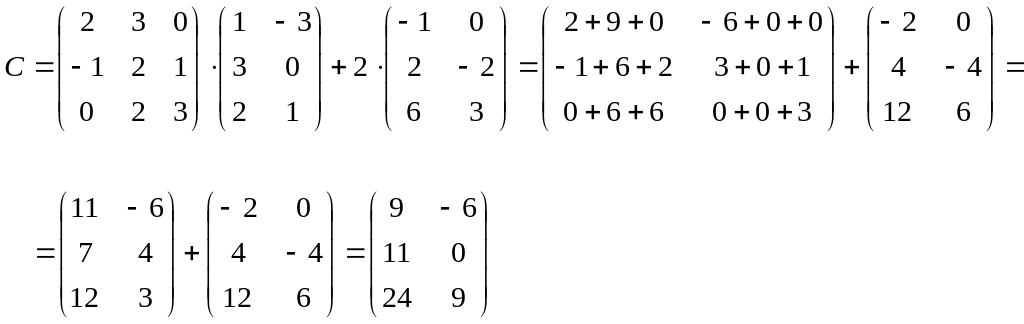
1. Определители квадратных матриц.

Для квадратных матриц вводится число, которое называется определителем.

Для матриц второго порядка ( размерность ) определитель задается формулой:

Например, для матрицы ее определитель

Пример. Вычислить определители матриц.

Для квадратных матриц третьего порядка (размерность ) существует правило «треугольника»: на рисунке пунктирная линия означает – умножить числа, через которые проходит пунктирная линия. Первые три числа надо сложить, следующие три числа надо вычитать.

Пример. Вычислить определитель.

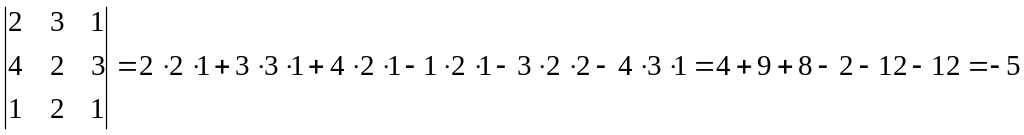
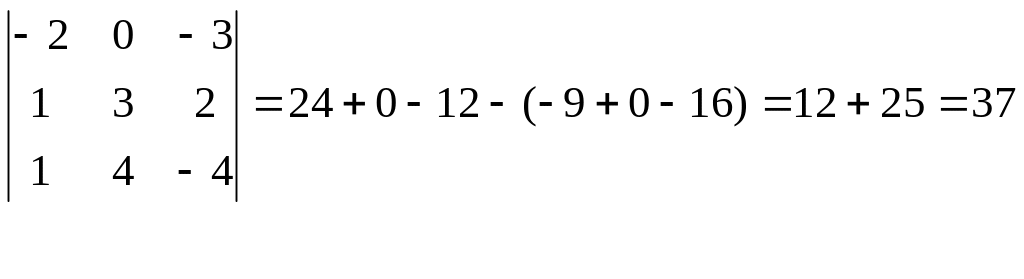
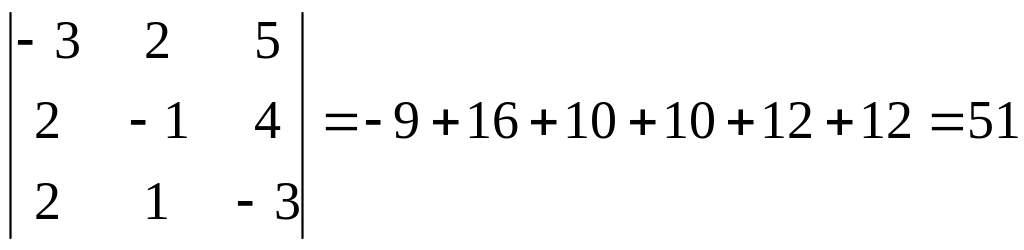
Чтобы дать общее определение определителя, надо ввести понятие минора и алгебраического дополнения.

Минором элемента матрицы называется определитель, полученный вычеркиванием - той строки и - того столбца.

Пример. Найдем некоторые миноры матрицы А.

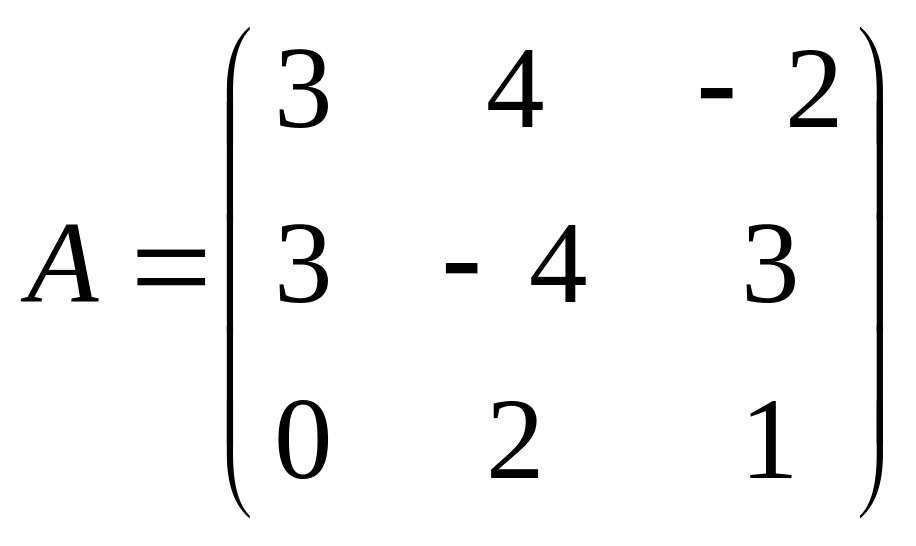
Алгебраическим дополнением элемента называется число .

Значит, если сумма индексов и четная, то и ничем не отличаются. Если же сумма индексов и нечетная, то и отличаются только знаком.

Для предыдущего примера .

Определителем матрицы называется сумма произведений элементов некоторой строки

( столбца) на их алгебраические дополнения. Рассмотрим это определение на матрице третьего порядка.

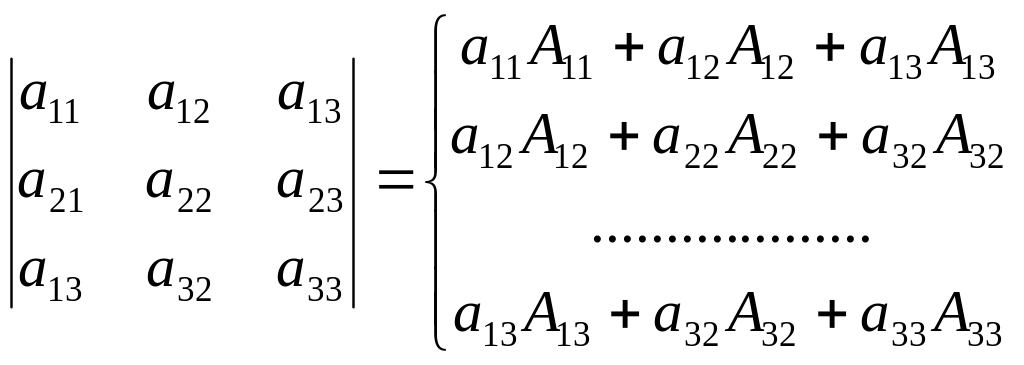
Первая запись называется разложением определителя по первой строке, вторая - разложение по второму столбцу, последняя – разложение по третьей строке. Всего таких разложений можно записать шесть раз.

Пример. Вычислить определитель по правилу «треугольника» и разложив его по первой строке, затем по третьему столбцу, затем по второй строке.

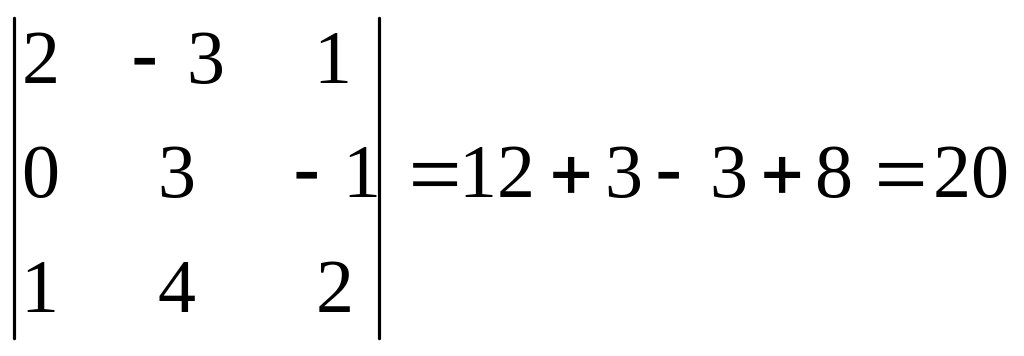
Разложим определитель по первой строке:

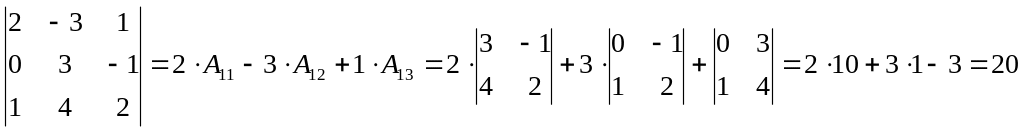
Разложим определитель по третьему столбцу:

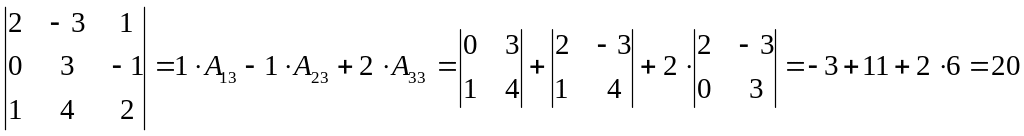
Разложим определитель по второй строке:

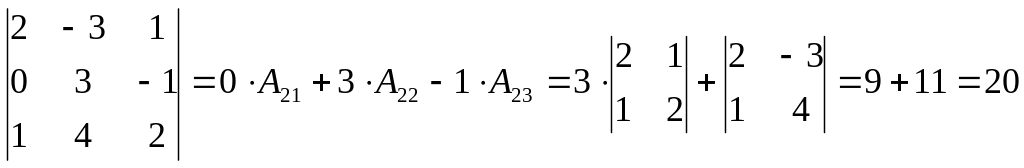
Заметим, что чем больше нулей, тем проще вычисления. Например, раскладывая по первому столбцу, получим

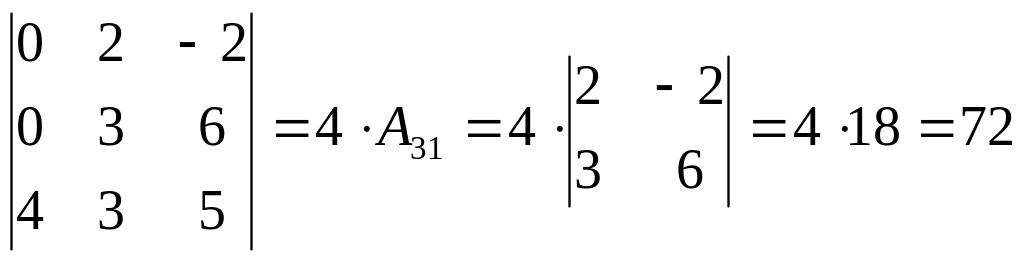
Среди свойств определителей есть свойство, позволяющее получать нули, а именно:

Если к элементам некоторой строки (столбца) прибавить элементы другой строки (столбца), умноженные на ненулевое число, то определитель не изменится.

.

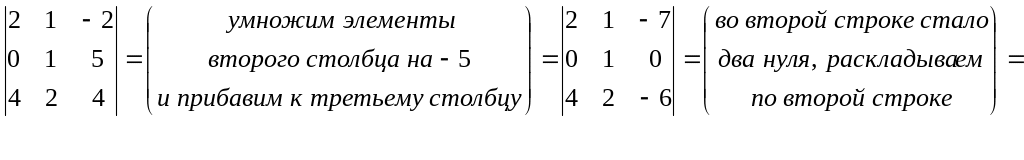
Возьмем этот же определитель и получим нули, например, в первой строке.

=

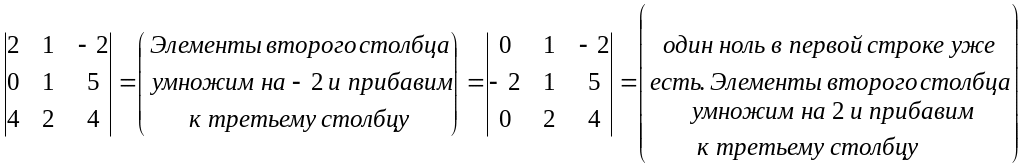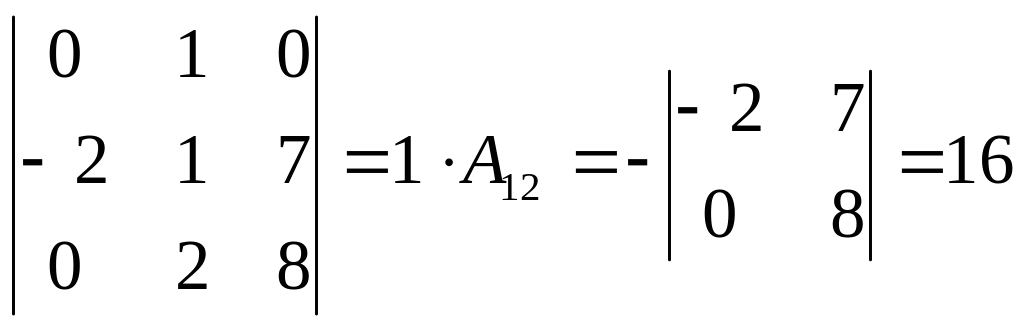
Определители более высоких порядков вычисляются таким же образом.

Задание 2. Вычислить определитель четвертого порядка:

1. разложив по любой строке или любому столбцу

2. получив предварительно нули

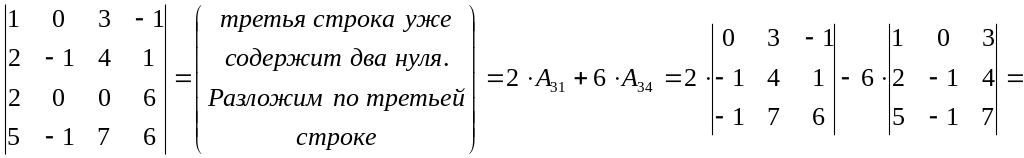
Получим дополнительный ноль, например, во втором столбце. Для этого элементы второй строки умножим на -1 и прибавим к четвертой строке: