Ответы на вопросы по вышей математике( Костюкович лекции):

1.Периодические функции. Ряд Фурье. Условие Дирихле.

Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода функции) на всей области определения.

Говоря более формально, функция называется периодической, если существует такое число T>0 (период), что на всей области определения функции выполняется равенство  .

Исходя из определения, для периодической функции справедливо также равенство  , где   - любое целое число.

Все тригонометрические функции являются периодическими.

Ряд Фурье — представление произвольной функции   с периодом   в виде ряда

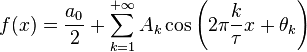
Этот ряд может быть также записан в виде

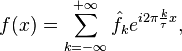
где

 — амплитуда  -го гармонического колебания,

 — круговая частота гармонического колебания,

 — начальная фаза  -го колебания,

 —  -я комплексная амплитуда

В более общем виде рядом Фурье элемента гильбертова пространства называется разложение этого элемента по ортогональному базису. Существует множество систем ортогональных функций: Уолша, Лагера, Котельникова и др.

Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.

Граничные условия Дирихле первого рода — тип граничных условий, названный в честь немецкого математика П. Г. Дирихле.^[1] Условие Дирихле, применённое к обыкновенным дифференциальным уравнениям или к дифференциальным уравнениям в частных производных, определяет поведение системы на границе области. Задача о нахождении таких условий называется задачей Дирихле.

2.Ряд Фурье для четных и нечетных функций на отрезке длинной 2П и для функций произвольных периода.

Для некоторых функций ряд упрощается.

Если ƒ(х) [-π;π] четная, то ;

Если функция – нечетная

Функция может быть задана на отрезке [a;a+2π]

В этом случае можно вычислять [0;2π]

Функция может иметь любой период l ƒ(x+l)=ƒ(x) [-l;l], в этом случае с помощью замены ( ; π) получаются след формулы

; f(x)=

Бывает, что ƒ(x) задано [0;π]. Возможно два вида продолжение в первом случае произойдет зануление по во втором случает получим зануление по

3. Комплексная форма ряда Фурье. Приложение рядов Фурье. Спектры.

Пусть   и   - коэффициенты Фурье функции  . На основании формул Эйлера

,

где (будем считать  ) .                                 

Отсюда

Эти два равенства можно записать в виде единой формулы

.              

Важно заметить, что если   - действительная функция, то   и   действительны, а числа   и  , хотя вообще и комплексны, но взаимно сопряжены:

.                                 

Очевидно,  -я сумма ряда Фурье функции   может быть записана в виде

,                       

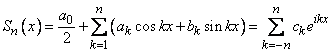а сам ряд Фурье функции   - в виде ряда

.               

Мы будем говорить, что ряд сходится для значения  , если существует предел

.

Таким образом определенная сходимость называется сходимостью в смысле главного значения.

Преобразование Фурье (ℱ) — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Преобразование Фурье функции   вещественной переменной является интегральным и задаётся следующей формулой:

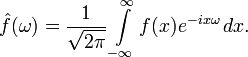
Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.

Мощным инструментом обработки данных, определённых дискретной зависимостью y(xi) или непрерывной функцией f(x), является спектральный анализ, имеющий в своей основе различные интегральные преобразования. Спектром совокупности данных y(x) называют некоторую функцию другой координаты F(ω), полученную в соответствии с определённым алгоритмом. Примерами спектров являются преобразование Фурье и вейвлетпреобразование. Каждое из интегральных преобразований эффективно для решения своего круга задач анализа данных.

Задачами, непосредственно связанными со спектральным анализом, являются проблемы сглаживания и фильтрации данных. Они заключаются в построении из исходной экспериментальной зависимости y(xi) некоторой (непрерывной или дискретной) зависимости f(x), которая должна приблизить её, учитывая к тому же, что данные (xi, yi) получены с некоторой погрешностью, выражающей шумовую компоненту измерений.

При этом функция f(x) с помощью того или иного алгоритма уменьшает погрешность, присутствующую в данных (xi, yi). Такого типа задачи называются задачами фильтрации. Сглаживание путём построения регрессии данных – это частный случай фильтрации.