23.Класификация операторов системы.

Оператор системы - это отображение , которое осуществляет система между входными и выходными переменными. Это их связь. Первый уровень классификации – по степени известности этой связи. Непараметризованный класс, когда об S известны только некие общие свойства (непрерывность, монотонность, симметричность, ...).

В параметризованном классе известен вид S с точностью до параметров – коэффициентов (например, y=ax+b, a, b - параметры).

Непараметризованный класс операторов системы (второй блок первого уровня) и соответствует подобным ситуациям с очень скудной априорной информацией об S.

Если эти параметры также заданы точно, то всякая неопределенность исчезает и мы имеем системы с полностью определенным оператором, т.е. “белый ящик”.

24.Вимірники системних параметрів

В

Трансп.мережа

Вхідні параметри

Вихідні параметри

имірювати системні параметри потрібно за допомогою якісних та кількісних вимірників. Якісні – вимірники, які характеризуються певним рівнем. Кількісні – виражаються цілочисельними показниками – певними показниками. Тобто, таким чином, для дослідження стану систем необхідно переходити від кількісних до якісних характеристик.

Пропускна спроможність, витрати на рух

Інтенсивність, швидкість, щільність

Кількісні показники

Рівень осблуговування

Якісні показники

Рівень якісної характеристики може зажди стати кількісним. Для цього необхідно ввести шкали. Якісні характеристики неможливо розрахувати за певними формулами. Їм можна лише дати оцінку.(приклад,високо\низько). Для того, об вирішувати дослідження запасів, переходів від якісних до кількісних вимірювачів іноді якісні вимірювачі простіше використовувати для аналізу параметрів функціонування системи. Наприклад, співвідношення інтенсивністі трансп.потоку до пропускної спроможності доріг виражається коефіцієнт завантаження доріг руху.

Числові характеристики бувають:

1.моментні – описує об’єкти у статиці(стан спокою) 2.інтервальні – у динаміці

Статична хар-ка системи – показує її стан і хар-ки функціонування за певний проміжок часу. Особливо важливим є моментна хар-ка.

Динамічна хар-ка – зміна параметрів у часі і просторі шляхом зміни цілочисельних показників. Важливим є інтервальна хар-ка.

Кількісні вимірники системних параметрів поділяються на прості, складні і структурні. До простих відносяться середнє арифметичне(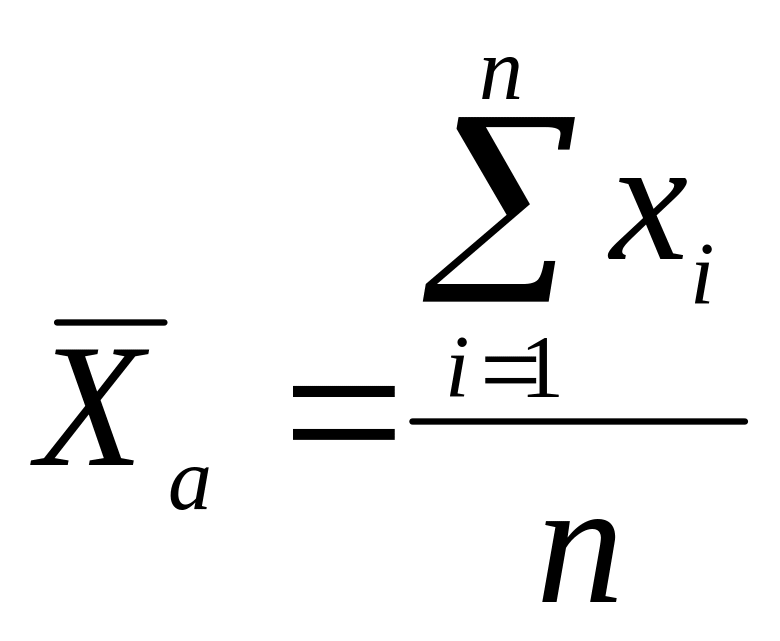 ), гармонічне() і геометричне( ). До складних відноситься середнє арифметичне зважене( ). До структурних відносяться мода і медіана.

Мода ( ) – одна з найважливіших характеристик сукупності, являє собою варіант, що найбільше часто зустрічається, у даному варіаційному ряді Медіана – значення ознаки, що варіює і доводиться на середину ранжируваної (упорядкованої) сукупності ( ). Медіана ділить ряд навпіл.

25. Відносні показники системи.

Відносні показники бувають прості, складні та структурні.

1.прості

- середнє арифметичне

( )

- гармонічне

- геометричне( )

2.Складні

арифметичне зважене( ).

3.Структурні

- Мода ( ) – одна з найважливіших характеристик сукупності, являє собою варіант, що найбільше часто зустрічається, у даному варіаційному ряді Наприклад - мода для ряду: 66 55 55 44 3 2 1 відповідає 5.

- Медіана – значення ознаки, що варіює і доводиться на середину ранжируваної (упорядкованої) сукупності ( ). Медіана ділить ряд навпіл. Наприклад – 66 55 431 (медіана – 5), якщо n – непарне число одиниць ряду, то медіана рівна середньої арифметичної із двох середніх значень варіантів: 6 6 5 5 5 5 4 4 3 1 .