Вопрос № 1

Система отсчета – совокупность систем координат и часов. С ним связано понятие тело отсчета – относительно него в пространстве, мы находим положение точки.

Траектория – линия, описываемая в пространстве движущейся точкой.

Длина пути – длина участка траектории, пройденной материальной точкой.

Перемещение – вектор, проведенный из точки начала движение в точку его нынешнего положения.

Вопрос № 2

Скорость – быстрота движения материальной точки, быстрота движения, направление в данный момент времени.

Ускорение – физическая величина, характеризующая быстроту изменения скорости по модулю и направлению.

Тангенциальное ускорение – это производная модуля скорости по времени.

Нормальное ускорение - ускорение характеризует быстроту изменения направления вектора скорости (характеризует изменение скорости по направлению

Вопрос № 3

Угловая скорость – называется векторная величина, определяемая первой производной угла поворота тела во времени.

Угловое ускорение – векторная величина, определяемая первой производной по угловой скорости по времени.

Связь угловой с линейной скоростью – линейная скорость равна произведению угловой на радиус.

Вопрос № 4

Связи между угловыми и линейными характеристиками движения материальной точки по окружности.

Период вращения - время одного оборота.

Частота вращения – число оборотов в единицу времени.

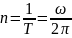
Центростремительное ускорение:

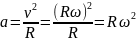
Угловая скорость:

При вращении вокруг фиксированной оси направление вращения может иметь только два значения: «по часовой стрелке» и «против часовой стрелки». Поэтому в этом случае можно говорить о двух знаках угловой скорости, обычно, плюс, при вращении против часовой стрелки и минус при вращении по часовой стрелке. 

Вопрос № 5

Первый закон Ньютона.

Гласит о том, что если в систему движения ничего не вмешивается, то оно находится в состоянии покоя или равномерного прямолинейного движения.

Инерциальная система отсчёта — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятся.

Вопрос № 6

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

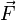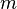• — ускорение тела,   — сила, приложенная к телу, а   — масса материальной точки

Вопрос № 7

Сила действия равна силе противодействия.

Как тело, которое прижимает к земле с силой = mg, а отталкивает N (нормальная реакция опоры).

Вопрос № 8

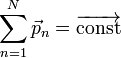
Закон сохранения импульса -  утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.

Другими словами – векторная сумма всех взаимодействий на тело = 0. Сколько пришло, столько и ушло.

Центр масс - геометрическая точка, характеризующая движение тела или системы частиц как целого. Другими словами – это материальная точка, имеющая массу, рассматриваемого в системе тела.

Вопрос № 9

Е

Энергия - скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.

А

F –сила, действующая на тело. S – перемещение, которое произошло от воздействия F.

Работа — величина являющаяся количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы и от перемещения точки, тела или системы.

N

Мощность - отношение работы, выполняемой за некоторый промежуток времени.

Вопрос № 10

 — масса тела

 — скорость центра масс тела

Кинетическая энергия - энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта.

Это энергия движущегося тела, равная и при отсутствии движения, нулю.

Потенциальная энергия – энергия тела, находящегося в поле притяжения на высоте h и обладающее массой m.

Вопрос № 11

Потенциальное поле - пусть взаимодействие тел, осуществляется посредством силовых полей, характеризующаяся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положения. Такие поля и есть потенциальные

Консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.

Вопрос № 12

Закон сохранения энергии - что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени.

Сколько было, столько и осталось, если его не трогают.

Вопрос № 13

Момент инерции – физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до оси.

Суммируется по все элементарным массам mi, на которое разбивается тело.

Вопрос № 14

Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.

Основные кинематические характеристики вращательного движения тела — его угловая скорость ( ) и угловое ускорение. 

, где I_z — момент инерции тела относительно оси вращения.

Вопрос № 15

Момент силы - векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению) на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

где   — сила, действующая на частицу, а   — радиус-вектор частицы.

Уравнение динамики вращательного движения твердого тела

,где J – главный момент инерции тела (момент инерции относительно главной оси)

E – угловое ускорение

Вопрос № 16

Момент импульса - характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

, где   — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,   — импульс частицы.

Закон сохранения – векторная сумма всех компонентов импульса, относительно заданной оси.

,  если система находится в равновесии.

Вопрос № 17

Деформация упругая – если после прекращения действия внешних сил тело принимает первоначальные размеры и форму.

Пластическая деформация – если после воздействия внешних сил, деформации сохраняются.

Закон Гука — утверждение, согласно которому деформация, возникающая в упругом теле, пропорциональна приложенной к этому телу силе. Закон Гука выполняется только при малых деформациях.

Вопрос № 18

Классическая теория тяготения — закон, описывающий гравитационное взаимодействие в рамках классической механики.

Теория гласит, что сила   гравитационного притяжения между двумя материальными точками массы   и  , разделёнными расстоянием  , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:

Здесь    — гравитационная постоянная.

Вопрос № 19

Сила тяжести — сила, действующая на любое материальное тело, находящееся вблизи поверхности Земли или другого астрономического тела.

По определению, сила тяжести на поверхности планеты складывается из гравитационного притяжения планеты и центробежной силы инерции, вызванной суточным вращением планеты.

Вес — сила воздействия тела на опору (или подвес или другой вид крепления), препятствующую падению, возникающая в поле сил тяжести

Невесомость — состояние, при котором отсутствует взаимодействие с опорой.

Вопрос № 20

 Силы тяготения являются консервативными. Это значит, что работа в поле этих сил пропорциональна произведению масс m и M материальных точек и зависит только от начального и конечного положения этих точек.

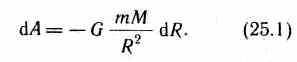Знак минус появляется потому, что сила и перемещение в данном случае противо­положны по направлению

Вопрос № 21

Первая космическая скорость – минимальная скорость, которую надо сообщить телу, чтобы оно находилось на орбите Земли.

Вторая космическая скорость – минимальная скорость, которую надо сообщить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спутник Солнца.

Третья космическая скорость -– минимальная скорость, которую надо сообщить телу, чтобы оно покинуло солнечную систему.

Вопрос № 22

Давление — физическая величина, численно равная силе F, действующей на единицу площади поверхности S перпендикулярно этой поверхности.

Закон Паскаля: давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях. Другими словами – если мы давим, то жидкость распирает во всех направлениях с одинаковой силой.

Закон Архимеда: на тело, погружённое в жидкость, действует выталкивающая сила, равная весу жидкости в объёме тела

где   — плотность жидкости ,  — ускорение свободного падения, а   — объём погружённого тела.

Вопрос № 23

Уравнения непрерывности — локальная форма законов сохранения.

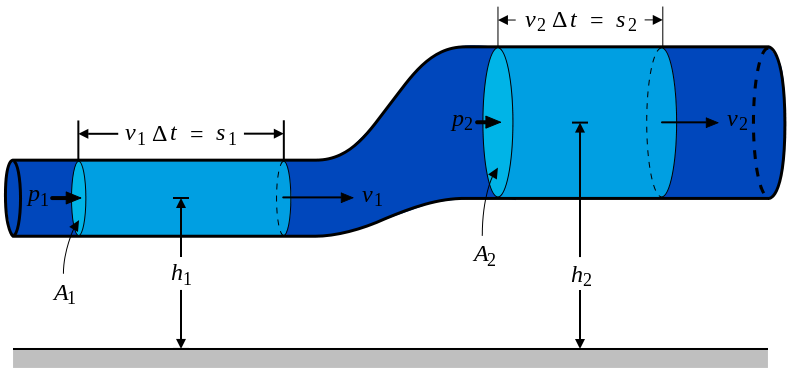
Если представить текущую жидкость, как реку, запертую в трубку, с сечением S и скоростью течения V.

Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки.

S1V1=S2V2=const – уравнение неразрывности

Вопрос № 24

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной несжимаемой жидкости:

Здесь

 — плотность жидкости,

 — скорость потока,

 — высота, на которой находится рассматриваемый элемент жидкости,

 — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

 — ускорение свободного падения.

Вопрос № 25

Формула Торричелли – связывает скорость истечения жидкости из малого отверстия в открытом сосуде с высотой жидкости над отверстием.

Формула Торричелли утверждает, что скорость   истечения жидкости через отверстие в тонкой стенке, находящееся в ёмкости на глубине   от поверхности, такая же, как и у тела, свободно падающего с высоты  , то есть

где   – ускорение свободного падения.

Вопрос № 26

Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по синусоидальному или косинусоидальному закону.

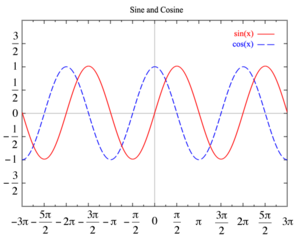
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Вынужденные колебания совершаются под воздействием внешней периодической силы.

Вопрос № 27

Дифференциальное уравнение, описывающее гармонические колебания, имеет вид

Любое нетривиальное^[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой 

Материальная точка совершает гармонические колебания, если они происходят в результате воздействия на точку силы, пропорциональной смещению колеблющейся точки и направленной противоположно этому смещению.

х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; ω — циклическая частота, величина, показывающая число полных колебаний, происходящих в течение 2π секунд;

Векторные диаграммы. Если представить гармоническое колебание в виде вектора, то их геометрическая сумма упростит нам жизнь сложения этих колебаний, как сумму векторов.

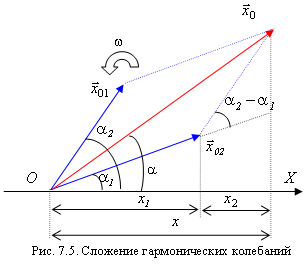
Вопрос № 28

Механические гармонические колебания

Тут надо рассказать про маятники.

Рассмотрим так называемый математический маятник - материальную точку, подвешенную на невесомой нерастяжимой нити и совершающую колебания в вертикальной плоскости под действием силы тяжести.

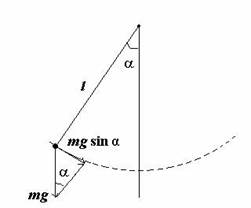
       Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:

где   — амплитуда колебаний маятника,   — начальная фаза колебаний,   — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется механическими гармоническими колебаниями.

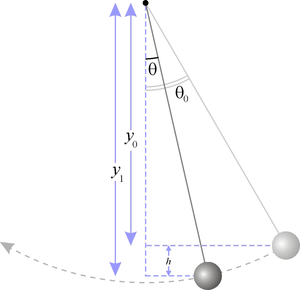
Кинетическая и потенциальные энергии здесь относятся к шарику.

Здесь для потенциальной энергия , h – это высота, на которой находится шарик, отклоненный от состояния покоя, если принять его состояние покоя за положение шарика внизу. Максимальна она при максимальном отклонении.

Здесь, для кинетической энергии , максимальную скорость он развивает в самом низу, соответственно и максимум находится там же.

Вопрос №29

Гармонический осциллятор — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x.

где k — коэффициент жёсткости системы.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания).

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости  k один конец которой жёстко закреплён, а на втором находится груз массы m. 

Математический маятник - осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения.

Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Вопрос № 30

Метод векторных диаграмм.

Смысл здесь в том, что мы просто представляем колебание, как вектор и, соответственно, сложение колебаний, сводится к сложению векторов.

Можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:

        Сопоставим этим колебаниям два вектора А₁ и А₂, вращающихся с соответствующими угловыми скоростями.

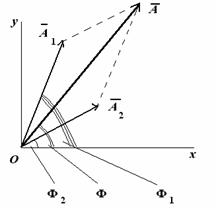
        Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f(фаза результирующего колебания).

        Из очевидных геометрических соображений находим: