Исследование эквивалентности непрерывного и дискретного звеньев сар
2.2.2. Z-преобразование
Для математического описания амплитудно-импульсных АИСАР и в частности их ветвей используется так называемое Z-преобразование.
Z-преобразование ставит во взаимнооднозначное соответствие результату дискретизации непрерывного сигнала (т.н. решетчатой функции) некоторую функцию комплексной переменной z:
(2.2)
где: x(iT) - значения амплитуд (точнее площадей) дискрет, полученных в результате дискретизации непрерывного сигнала.
Правая часть (2.2) представляет собой бесконечный ряд, сходящийся к функции X(z).
Z-преобразование - линейное. Это означает, что изображение суммы оригиналов равно сумме изображений каждого из них, и масштабному изменению величины оригинала (умножению на коэффициент) соответствует пропорциональное изменение изображения:
(2.3)
Обратное Z-преобразование Z-1{X(z)} позволяет по Z-изображению X(z) получить оригинал, т.е. решетчатую функцию x(iT), сгладив которую можно получить непрерывный сигнал.
Примечание. Z-преобразование может быть осуществлено только над функцией x(t), значения которой известны на всем протяжении времени от минус до плюс бесконечности, т.е. апостериорно, например для пробных сигналов. Работать в реальном времени, по мере поступления значений непрерывного сигнала Z-преобразование, как и преобразование Лапласа, не способно (см. [1]).
Т.о. Z-преобразование ставит в соответствие бесконечному набору дискрет, следующих во времени друг за другом, и представляющих, заменяющих собой непрерывную функцию времени x(t), некоторую непрерывную, дробно-рациональную функцию X(z), с которой удобно работать. Обратное преобразование по функции X(z) позволяет получить решетчатую функцию x(iT).
Существуют таблицы Z-преобразования различных функций времени. Кроме того, в настоящее время для получения Z-изображений и оригиналов удобно пользоваться Маткадом:
Обратное Z-преобразование позволяет получить решетчатую функцию по ее Z-изображению. Это преобразование можно осуществить в Маткаде или выполнить путем разложения Z-изображения в степенной ряд по z-1 с последующей заменой аргумента на iT: Как видно, из полученной в результате обратного Z-преобразования решетчатой функции нетрудно получить значение соответствующей ей непрерывной функции. Тот же результат получается при разложении Z-изображения сигнала в степенной ряд по z-1, например делением числителя Z-изображения на знаменатель.
2.2.3. Z-передаточная функция типовой ветви АИСАР
Типовая ветвь АИСАР, как было показано на рис 2.8, имеет вид:
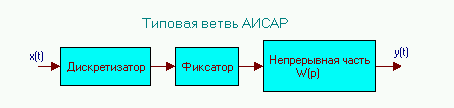
Рис.2.8, а. Типовая ветвь АИСАР преобразует непрерывный сигнал в решетчатую функцию (дискретизирует), осуществляет фиксацию и затем преобразует сигнал линейной инерционной непрерывной частью
Типовая ветвь АИСАР описывается дискретной Z-передаточной функцией:
(2.4)
Формально, эта передаточная функция связывает решетчатую функцию выходного сигнала с решетчатой функцией входного. Но при выборе достаточно малого периода дискретизации, эту функцию с практической точки зрения можно трактовать и как оператор преобразования непрерывного входного сигнала в непрерывный выходной. Это полезно в отношении перенесения свойств непрерывных САР на АИСАР, содержащие ветви с дискретизаторами.
Т.о. Z - преобразование и преобразования Лапласа схожи в том смысле, что как одно, так и другое позволяет ставить в соответствие функции времени ее изображение, а для ветвей САР и АИСАР записывать передаточные функции, с помощью которых можно определять выходной сигнал ветви при известном входном. Естественно изображения одного преобразования отличаются от изображений другого (см. табл. на рис. 2.9).
Между Z-передаточной функцией типовой ветви АИСАР и передаточной функцией W(p) ее непрерывной части имеется взаимнооднозначное соответствие.
Z - передаточную функцию типовой ветви АИСАР по характеристикам непрерывной части этой ветви можно найти различными способами, в частности по формуле [3]:
(2.5)
где hн(t) -переходная функция непрерывной части ветви.
Или, без учета фиксатора, по приближенной формуле
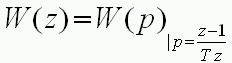(2.6)
Для учета фиксатора правую часть (2.6) нужно домножить на специальный коэффициент, определяемый периодом дискретизации.
Более точный переход от непрерывной системы к системе дискретной во времени дает т.н. подстановка Тастина [3]:
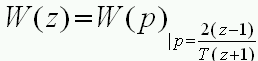(2.7)
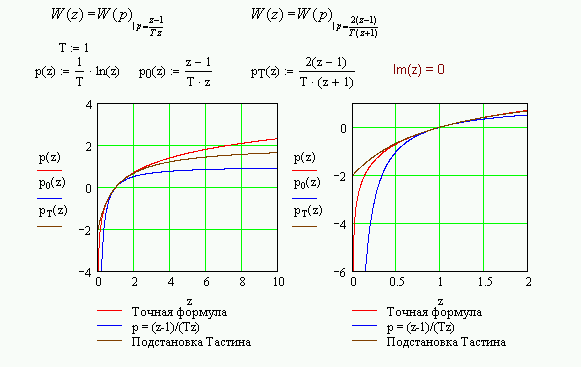
Рис.2.13. Иллюстрация точности замены точной формулы перехода от передаточной функции непрерывной части типовой ветви АИСАР к ее Z-передаточной функции приближенными при действительном аргументе. Как видно, точность аппроксимации в диапазоне изменения z от 0.5 до 2 хорошая
Отметим, что коэффициенты полиномов числителя и знаменателя Z-передаточной функции конкретной АИСАР зависят от периода дискретизации. Поэтому даже при небольшом изменении значения периода будут получаться другие выражения для передаточной функции, но описывать они будут ту же самую непрерывную ветвь или АИСАР целиком.
.