
- •1. Предел функции.
- •2. Односторонние пределы функций.
- •Задания для самостоятельной работы.
- •Свойства пределов функций.
- •4. Бесконечно малые и бесконечно большие функции.
- •5. Некоторые приемы вычисления пределов
- •1) Неопределённость вида . Отношение многочленов.
- •Задания для самостоятельной работы.
- •2) Неопределённость вида , содержащая иррациональность.
- •Задания для самостоятельной работы.
- •3) Неопределённость вида . Отношение многочленов. Иррациональность.
- •Задания для самостоятельной работы.
- •6. Непрерывность функции в точке.
- •Задания для самостоятельной работы.
- •7. Первый замечательный предел.
- •Задания для самостоятельной работы.
- •8. Второй замечательный предел.
- •Задания для самостоятельной работы.
Задания для самостоятельной работы.
Найти предел дроби 1)
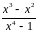 ,
2)
,
2)
 ,
,
если
а)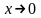 ,
б)
,
б) ,
в)
,
в) .
.
2.
 .
3
.
3

4.
 .
5.
.
5.

6.
 7.
7.

8.
 .
9.
.
9.
 .
.
10.
 .
11.
.
11.
 .
.
2) Неопределённость вида , содержащая иррациональность.
Пусть
неопределённость вида
содержит
иррациональность в числителе. Следует
перенести её в знаменатель, умножая и
числитель, и знаменатель на выражение,
дополняющее разность корней
 до разности
до разности
 .
Напомним, что из формул сокращенного
умножения следует, что для этого
.
Напомним, что из формул сокращенного
умножения следует, что для этого
 надо
умножить на
надо
умножить на
 ,
,
 надо
умножить на
надо
умножить на
 ,
,
 надо
умножить на
надо
умножить на
 …
…
Пример
1.
Вычислить
 .
.
Решение.
От
иррациональности в числителе избавляет
операция
 .
Значит,
.
Значит,

Пример
2.
.
Вычислить
 .
.
Решение.
Здесь
от иррациональности в числителе
избавляемся, умножая на неполный квадрат
суммы:
 .
.
Возвращаясь к пределу, получаем

Пример
3.
Вычислить

Решение. Множим числитель на неполный квадрат разности:
 .
.
Тогда
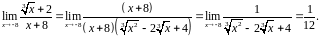 ▲
▲
Аналогично поступаем, когда иррациональность в знаменателе.
Пример
4. Вычислить
 .
.
Решение. Здесь от иррациональности в знаменателе избавит операция
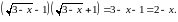 Поэтому
Поэтому

Пример
5.
Найти
 .
.
Решение. От иррациональности в знаменателе избавит операция
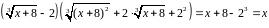 .
Поэтому
.
Поэтому
 ▲
▲
Пример
6.
Найти
 .
.
Решение. Избавляемся от иррациональности:
для
числителя

для
знаменателя
 .
.
Окончательно
 ▲
▲
Задания для самостоятельной работы.
1.
 2.
2.

3.
 4.
4.

5.
 6.
6.

7.
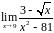 8.
8.

9.
 10.
10.

3) Неопределённость вида . Отношение многочленов. Иррациональность.
Исследуем
поведение многочлена
 при стремлении аргумента
к
при стремлении аргумента
к
 .
После преобразования
.
После преобразования

становится
очевидным (теоремы о пределе суммы и
произведения), что
 ,
знак при
,
знак при
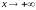 зависит только от знака старшего
коэффициента
зависит только от знака старшего
коэффициента
 ,
а при
,
а при

от знака
и от чётности степени многочлена
от знака
и от чётности степени многочлена
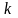 .
.
Пример
1.
Как ведут себя многочлены
 и
и
 при стремлении аргумента
к
?
при стремлении аргумента
к
?
Решение.
1)
 ,
,
т.к.
выражение в скобках стремится к 2>0, а
множитель
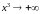 .
.
2)
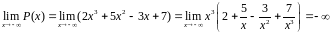 ,
,
здесь
знак результата определяет множитель
 .
.
3)
 ,
,
т.к.
выражение в скобках стремится к 5<0,
а множитель
 .
.
4)
 ,
,
здесь
знак результата в силу чётности множителя
 опять определяет знак старшего
коэффициента. ▲
опять определяет знак старшего
коэффициента. ▲
Таким образом, при стремлении аргумента к вычисление предела отношения двух многочленов всегда приводит к неопределённости вида .
Пример
2.
Найти а) б)
б)
 .
.
Решение.
а)
Вынесем за скобки и в числителе, и в
знаменателе старшую степень
 :
:
 .
.
После
сокращения на
неопределённости не осталось: теперь
и числитель, и знаменатель по теореме
о пределе суммы при
 имеют конечные пределы, причём предел
знаменателя равен
имеют конечные пределы, причём предел
знаменателя равен
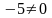 .
В силу теоремы о пределе частного
.
В силу теоремы о пределе частного
 .
.
б) Вынесем за скобки старшую степень числителя :

 .
.
Теперь и числитель, и знаменатель при имеют конечные пределы, но предел знаменателя (суммы трёх бесконечно малых) равен нулю. Так как знаменатель бесконечно малая при функция, то частное бесконечно большая функция:

При
наличии иррациональности неопределённость
раскрывается так же, как и для натурального
аргумента
 .
.
Пример
3. Найти
предел функции
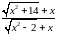 при
.
при
.
Решение. Данная функция при есть отношение двух бесконечно больших функций (неопределенность вида ). После того, как разделим и числитель, и знаменатель на (старшую степень), проблем не остается:
 .
▲
.
▲
Пример
4. Найти
 =
.
=
.
Решение.
В
числителе старшая степень равна
 ,
в знаменателе старшая степень
тоже
.
Разделим на
,
в знаменателе старшая степень
тоже
.
Разделим на
 и числитель, и знаменатель:
и числитель, и знаменатель:


 .
.
Теперь
и числитель, и знаменатель имеют при
конечные пределы, причём предел
знаменателя равен
 .
В силу теоремы о пределе частного
получаем
.
В силу теоремы о пределе частного
получаем
 .
▲
.
▲
Пусть
 и
и
 ,
тогда
,
тогда

При
 этот результат был получен ранее, когда
аргументом было натуральное число
этот результат был получен ранее, когда
аргументом было натуральное число
 ,
а не непрерывно изменяющаяся переменная
.
,
а не непрерывно изменяющаяся переменная
.
Пример
5. Найти
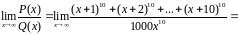
Решение.
Степени
многочленов
 и
и
 одинаковы, поэтому предел равен отношению
коэффициентов при старших степенях.
Так как в числителе слагаемое
одинаковы, поэтому предел равен отношению
коэффициентов при старших степенях.
Так как в числителе слагаемое
 повторяется 10 раз, получаем
повторяется 10 раз, получаем
 .
▲
.
▲
Пример
6. Найти
 .
.
Решение. Раскрывая скобки, преобразуем числитель к виду
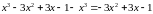 ,
,
а
знаменатель – к виду
 .
.
Получаем
 .
Степени числителя и знаменателя
одинаковы, поэтому предел равен отношению
коэффициентов при старших степенях:
.
Степени числителя и знаменателя
одинаковы, поэтому предел равен отношению
коэффициентов при старших степенях:
 .▲
.▲
Пример
7. Найти

 .
.
Решение. Чтобы определиться со старшей степенью числителя и знаменателя, воспользуемся биномом Ньютона:
 ;
;
 Оказалось,что
степени многочленов
и
одинаковы, поэтому предел равен отношению
старших коэффициентов:
Оказалось,что
степени многочленов
и
одинаковы, поэтому предел равен отношению
старших коэффициентов:
 .▲
.▲
Неопределённость
 сводится к неопределённости
или
.
сводится к неопределённости
или
.
Пример
8. Вычислить
 .
.
Решение.
 .
▲
.
▲
Пример
9.
Вычислить
 .
.
Решение.

 .
▲
.
▲
Пример
10. Вычислить
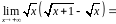 .
.
Решение.
 .
▲
.
▲
