§ 73. Условие эволюционности ударных волн

Для возможности реального существования гидродинамический разрыв должен быть устойчив относительно расщепления на два или более других разрывов. Это условие можно иначе сформу­лировать как требование, чтобы любое бесконечно малое возму­щение начального состояния приводило бы лишь к бесконечно малым же изменениям разрыва; удовлетворяющие этому требова­нию разрывы называют эволюционными. Подчеркнем, что свойство эволюционности отнюдь не совпадает с устойчивостью в обычном смысле этого слова. Обычная неустойчивость означает постепен­ное возрастание начального малого возмущения, приводящее в конце концов к разрушению данного режима движения; но даже при экспоненциальном (как е*", у > 0) возрастании в течение достаточно малого промежутка времени (t^.l/y) воз- мущение остается малым. В неэволюционном же разрыве воз- мущение сразу делается большим в(я) ш—р(х) (хотя при малых t оно и занима- I ет еще малую область простран-

I ства). Это иллюстрируется рисун-

-~ ком, на котором изображено рас-

мущепление скачка плотности р (х) #р на два последовательных скачка

(рис. 41); возмущение бр не мало, I хотя и занимает при малых t (ког-

да оба разрыва еще не разошлись ⁴¹' на заметное расстояние) лишь ма-

лый интервал 8х. Критерий эволюционности можно получить путем подсчета числа независимых параметров, определяющих произвольное на­чальное (при / = 0) малое возмущение разрыва, и числа уравне­ний (линеаризованных граничных условий на разрыве), которым они должны удовлетворять. Разрыв эволюционен, если оба числа одинаковы; тогда граничные условия однозначно определяют дальнейшее развитие возмущения, которое при малых t > 0 оста­нется малым¹). Если же число уравнений больше или меньше числа неизвестных параметров, то задача о малом возмущении разрыва не имеет решения вовсе или имеет их бесконечное мно­жество. Ни то, ни другое невозможно, и такая ситуация будет свидетельствовать о неправомерности исходного допущения (ма­лость возмущения при малых /); разрыв неэволюционен.

В обычной гидродинамике требование эволюционности удар­ных волн не приводит к каким-либо дополнительным ограниче­ниям по сравнению с условием возрастания энтропии: ударные волны, допускаемые теоремой Цемплена, автоматически эволю-ционны (см. VI § 84). В магнитной гидродинамике это не так, и требование эволюционности налагает новые существенные огра­ничения на характер изменения величин в ударной волне (А. И. Ахиезер, Г. Я. Любарский, Р. В. Половин, 1958)²).

⁵) При этом волна может быть как неустойчивой (если среди собственных частот уравнений имеются комплексные с положительной мнимой частью), так и устойчивой (если таких частот нет).

³) Что касается других магнитогидродинамических разрывов (контактных, тангенциальных, альфвеновских), то онн оказываются всегда эволюционными.

Приступая к фактическому выяснению условия эволюционности магнитогидродинамических ударных волн, подсчитаем прежде всего число уравнений, которым должно удовлетворять произ­вольное малое возмущение на поверхности разрыва.

Будем представлять себе ударную волну как плоскую и вы­берем ее плоскость в качестве плоскости yz. Положительное на­правление оси х выберем в сторону движения гага через поверх­ность разрыва. Невозмущенные поля Я₁₍ Я₂ и скорости газа rj₁₍ rj₂ по обе стороны разрыва пусть лежат в плоскости ху.

С каждой стороны поверхности разрыва подвергаются возму­щению семь величин: три компоненты скорости жидкости (v_x, v_y, v_z), две компоненты магнитного поля (Н_у, Я_г), плотность р=1/1/ и энтропия s. Возмущения остальных термодинамических величин (Р, ш) определяются возмущениями р и s. В силу уравнения div Н = дН_х1дх — 0 продольная компонента поля Н_х постоянна вдоль оси х и возмущению не подвергается. Кроме того, возму­щению подвергается скорость распространения самой ударной волны, т. е. у нее появляется малая скорость (обозначим ее 6U) по отношению к выбранной системе координат (в которой невоз­мущенный разрыв покоится). Эта скорость, однако, может быть сразу выражена через возмущения р и v_x из условия непрерыв­ности плотности потока массы / через разрыв. Действительно, скорость газа относительно разрыва есть

где v_x0 — невозмущенная скорость, 6v_x—ее возмущение; написав также р = р₀ + бр, линеаризовав граничное условие {/} = 0 и опу­стив затем индекс 0 у невозмущенных величин, получим

откуда определяется 6U.

Линеаризация граничных условий непрерывности компоненты U_zx потока импульса и компоненты Е_у электрического поля (т. е. 2-компонент уравнений (70,4—5)) дает два уравнения

{(*>М-ъ Я_жбЯ,} = 0, {Н_х 8v_z-v_x 8H_Z} = 0

(напомним, что невозмущенные значения u_z = 0, Я_г = 0). Эти уравнения содержат возмущения только двух величин:

Ч. ^б#₂- (73,1)

Граничные же условия непрерывности потока энергии q_x, компо­нент П^, П_ух потока импульса и компоненты Е_г электрического поля (т. е. уравнения (70,2—3) и г/-компоненты уравнений (70, 4—5)) дают четыре линейных уравнения, которые содержат возмущения

6v_x, 6v_y, бН_у, бр, 6s; (73,2)

мы не будем выписывать их здесь.

Подсчитаем теперь число параметров, определяющих возму­щение ударной волны. Возмущения, зависящие от времени как е~^ш, распространяются в обе стороны от разрыва в виде магнита­

гидродинамических волн трех видов (альфвеновские, быстрые и медленные магнитозвуковые) и в виде энтропийной волны; последняя представляет собой малое возмущение энтропии, ко­торое (в силу адиабатичности течения газа) переносится вместе с самим газом, с его скоростью. При этом все эти волны должны, конечно, быть уходящими — распространяться влево или вправо от разрыва. В каждой волне изменения всех величин связаны друг с другом определенными соотношениями (как это было по­казано в § 69); поэтому каждая волна определяется всего одним параметром — амплитудой какой-либо одной величины.

Магнитозвуковые и энтропийные волны переносят возмущения (73,2), а альфвеновские волны — возмущения (73,1). Поскольку уравнения для этих двух групп возмущений разделяются, то условие эволюционности должно быть выполнено для каждой из них в отдельности (С. И. Сыроватский, 1958); это обстоятельство еще усиливает возникающие ограничения.

Рассмотрим сначала условия эволюционности относительно альфвеновских возмущений. Оно требует, чтобы число уходящих волн равнялось двум—по числу уравнений. Фазовые скорости альфвеновских волн относительно поверхности разрыва могут быть равны

V_xl ± Ид₁₍ V_x2 ± И_А2,

где «д—фазовая скорость (69,6) волны относительно газа. По условленному выбору направления оси х скорости газа v_xl, v_x2 > 0. В области 1 перед разрывом волна уходит от него, если ее фа­зовая скорость (относительно разрыва) отрицательна, а в области 2 позади разрыва—если она положительна. Волна со скоростью v_xl-\-u_Al этому условию никогда не удовлетворяет (она всегда

приходящая), а волна со скоростью _v v_xi — Uai—уходящая npuv_xl < u_Al.

^nt Аналогичным образом волна со

«А1

"иг

скоростью v_x2-\-и_А2 всегда уходя­щая, а со скоростью v_x2 — и_А2—ухо­дящая при v_x2 >Ыд₂. Поэтому суще­ствуют две области эволюционно­сти относительно альфвеновских волн:

1. V_xl > U_Au V_x2 > Ид₂,

2. v_xl < U_Al, V_x2 < И_А2-

^ин1

"£7

Рис. 42.

Эти области отмечены на рис. 42 вертикальной штриховкой;рисунок построен с учетом неравенств

^{"м < "а < "б- (73,3)}

Условие эволюционности по отношению к магнитозвуковым и энтропийным возмущениям требует, чтобы число уходящих волн было равно четырем. Уходящая энтропийная волна, пере­мещающаяся вместе с газом, всегда существует, но только со сто­роны 2. Число уходящих магнитозвуковых волн должно поэтому быть равно трем. Рассуждения, подобные проведенным выше для альфвеновских волн, приводят к двум областям эволюционности по отношению к рассматриваемой группе возмущений, показан­ных на рис. 42 горизонтальной штриховкой¹).

Пересечение обеих штриховок определяет две области эволю­ционности относительно всех возмущений: 1) быстрые ударные волны, для которых

v„i > u_6l, «_б2 > v_n2 > и_А2, (73,4)

и 2) медленные ударные волны, для которых

"At > f„i > "„1. "м2 > v_n2 (73,5)

(мы вернулись к обозначению нормальной компоненты скорости газа как v_n вместо v_x). В предельном случае слабой интенсивности волны (малые скачки всех величин) быстрые и медленные ударные волны распространяются со скоростью соответственно и_б2« и и_ма«и_м1.

Применим полученные условия эволюционности к выяснению характера изменения магнитного поля в ударной волне. Исходим из равенства (72,2)

Й {НЛ = {^}=}КН_<}

или

(w-°"0^Hw=(^-^o"'b'- ^(73,6)

Заметив, что Щ/Апр = и\, можно иначе переписать его в виде

4i-&_H u\₂-v%₂

v„i ¹¹ v_ni ⁿ ^ > >

С учетом неравенств (73,4—5) из (73,7) видно, что тангенци­альные поля по обе стороны ударной волны не только коллине-арны, но и направлены в одну сторону.

В медленных ударных волнах с обеих сторон разрыва

4л/ v_n

Заметив также, что из непрерывности потока массы, p!V_nl = p₂v_n2, и из неравенства р_х < р₂ следует, что

¹) Отметим, что среди областей неэволюционности существуют случаи, когда число параметров как больше, так и меньше числа уравнений,—по каждой из двух групп возмущений.

о»1 > »„., (73,8)

заключаем из (73,6), что Н_п < Н_п—в медленной ударной волне тангенциальное магнитное поле ослабляется. В быстрой же волне v_ny #Л/4я/ и из (73,6) следует, что #_f2 > #_п— тангенциальное магнитное поле усиливается.

Отметим частный случай ударных волн, в котором магнитное поле с обеих сторон поверхности разрыва параллельно нормали к ней. Как было указано в начале § 72, всегда можно выбрать систему координат таким образом, чтобы с обеих сторон векторы v и Н были параллельны друг другу. Тогда в рассматриваемом случае будет

H»i=H_f2 = 0, v_n = v_f2 = 0

(параллельная ударная волна). Для такой волны граничные усло­вия вообще не содержат магнитного поля, т. е. совпадают с гра­ничными условиями для ударной волны в обычной гидродинамике. Наличие магнитного поля приводит, однако, к тому, что в оп­ределенном интервале значений параметров волны нарушаются условия эволюционности и такие волны становятся невозможными (см, задачу).

Что касается рассмотренных в конце предыдущего параграфа перпендикулярных ударных волн, то все такие волны сжатия эволюционны, причем они являются быстрыми волнами. Последнее очевидно уже из того, что при #„ = 0 скорости и_А = и_м = 0.

Рассмотрев различные типы разрывов в магнитной гидроди­намике, остановимся еще на вопросе о возможности существова­ния переходных случаев между этими типами, т. е. разрывов, которые обладали бы одновременно свойствами двух типов. Такие возможности сильно ограничены условиями, вытекающими из требования эволюционности.

Прежде всего, альфвеновский разрыв не может непрерывно перейти в ударную волну. Действительно, в ударной волне нор­маль к поверхности разрыва и магнитное поле по обе ее стороны лежат в одной плоскости. Такая ударная волна может совпасть с альфвеновским разрывом, только если в нем вектор Н пово­рачивается на 180°. Но тогда тангенциальная компонента поля меняет знак, между тем как в эволюционной ударной волне она не меняет знака.

Между быстрой и медленной ударными волнами непрерывный переход был бы возможен только при Н_п = Н₍₂ = 0, так как в быстрой волне поле H_t (если оно отлично от нуля) усиливается, а в медленной — ослабляется; другими словами, непрерывный переход мог бы быть только между параллельными быстрой и медленной волнами. Но области эволюционности этих волн соприкасаются только при u_Al = u₀₁, когда медленная волна ис­чезает (см. задачу 1). Таким образом, непрерывный переход между быстрыми и медленными ударными волнами невозможен.

Быстрая волна не может непрерывно перейти в тангенциаль­ный разрыв в силу неравенств (73,4).

Таким образом, возможны непрерывные переходы лишь между тангенциальным разрывом, с одной стороны, и контактным раз­рывом, альфвеновским разрывом или медленной ударной волной — с другой.

Задачи

1. Найти область значений г\, в которой нарушается эволюционность параллельной ударной волны в идеальном (в термодинамическом смысле) одноатомном газе с отношением теплоемкостей c_p/c_v = ~°/₃.

Решен и е. Для указанного газа тепловая функция ау=5Я/2р и система граничных условий (70,1—3) принимает вид

-Paol.

2 "1-

Pi

Pa

Отсюда находим

2

(где «„= (5P/3p) '²—обычная скорость звука) и далее:

Зи„

У Р2 "^Al~ 2UT

*Al-

4oi

'Ai

= min («„{,

= min («₀₂,

"61 '^Лб2 ⁼

= max (u₀i, ; max (u₀2>

«Al)- ¹

"Аг). "м2— """ ("02, "да При «_Al < «oi условия эволюционности всегда выполняются, причем удар­ная волна является быстрой. На рис. 43 изображен примерный вид зависи­мостей v₂(v₁) (жирная линия) и u_A2(v_t), «_б2 (^i) = и₀2 (^yi) ^{в этом} случае; на­клонная штрихпунктирная прямая — биссектриса прямого угла.

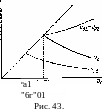На рис. 44 изображена аналогичная диаграмма для случая «_Al > и_а\. Тонкие линии — снова зависимости н_д (v_{) и «₀₂(U|); на различных участках этих линий указано, какая из скоростей, «_б2 или «_ма, с ними совпадает.

Жирная сплошная линия — зависимость v₂ (v_x) в областях эволюционности, причем левая ее часть отвечает медленным, а правая — быстрым ударным волнам. Жирный пунктир — неэволюционный участок, занимающий интервал

^ttAi <^vi< У^им — 3«oi;

он ограничен справа точкой, в которой у₂ = «_а2¹)-

2. Впереди ударной волны тангенциальное магнитное поле Нд = 0, а по­зади Н(₂ Ф 0 (такую ударную волну называют волной включения). Найти ин­тервал значений скорости v_nl, которой может обладать такая волна в газе с теми же термодинамическими свойствами, как и в задаче 1.

Решение. Из (72,2) следует, что при Н^=0 скорость волны относи­тельно газа позади нее:

^уп2 = ^_п/у^Г4яр₂ = и_А2, а относительно газа впереди:

^1 = -^^2 = "_А1]/^ > «_А1.

Эта волна —быстрая; v_nl и v_n2 связаны друг с другом соотношением v_nlv_n2 = u²\i²)-Для волны включения в газе с указанными термодинамическими свойст­вами из граничных условий можно получить

Н% Pi / 2 2 \ /,,,,2 „2 2 \

-jr- = -^EV" "Al) (4UA!— зйо1 — Vrn).

3«Ai

Поскольку правая сторона равенства должна быть положительна и поскольку ^vni > ^и \i> ^{то мы ВИ}Д^ИЫ. что возможные значения v_nX в волне включения ограничены интервалом

«А^^ТЛ^-Зи².!.

Как видно из этих неравенств, волны включения возможны только при ^uAi ^> "⁰¹" ^^а Р^ис' ^ ^{этим волнам} отвечает отрезок тонкой сплошной линии, отмеченный буквами ВВ.