§ 4. Проводящий эллипсоид

Задача об определении поля заряженного проводящего эллип­соида и задача об эллипсоиде во внешнем однородном поле ре­шаются с помощью так называемых эллипсоидальных координат.

Связь эллипсоидальных координат с декартовыми дается уравнением

~гт—г-т/г-Ч-т^—= 1 (а>Ь>с). (4,1)

Это уравнение, кубическое относительно и, имеет три различных вещественных корня (и = %, у\, £), лежащих в следующих интер­валах:

1>—с², — с²>г]>—Ь², — Ь²>£>—а². (4,2)

Эти три корня и являются эллипсоидальными координатами точки х, у, г. Их геометрический смысл явствует из того, что поверхности постоянных значений Е, г\, £ представляют собой соответственно эллипсоиды, однополостные гиперболоиды и двух-полостные гиперболоиды, причем все они софокусны с эллипсоидом

Через каждую точку пространства проходит по одной поверх­ности этих трех семейств, причем эти поверхности взаимно орто-С тональны. Формулы преобразования от эллипсоидальных коор­динат к декартовым получаются путем совместного решения трех

уравнений типа (4,1) и имеют вид

'д + а¹) (П + «^г) (£ + а^г)

У=± г = ±

(б² —а²) (с²—а²) (£ + 6')(Л+6')(£+6'У

(4,4)

(с² — &²) (а² —б²) (g + c²) (п+с*) (£ + с²)

(а² —с²) (б² —с²)

]A(ti-C) (т)-Е)

V(£-л) (6-5)

A₂ =

Элемент длины в эллипсоидальных координатах имеет вид d/² = hldl² + hid Ti² + НЩ\

ho

2Я_Р

(4,5)

где введено обозначение

R_a=V(u + a*) (u + b>) (ы + с²), ы = 1, ti, J. Соответственно, уравнение Лапласа в этих координатах есть

Дер:

(6-л) Й-

-I) (л-С)

51

5ф

+

^{+ (С-Е) /?}_ч^{^ (*„ ^) + (Е -л) *}₆^{£ (/?}_е ^{f ) J = о- (4,6)}

Е сли две из полуосей а, Ь, с становятся равными, то эллип­соидальная система координат вырождается. Пусть а = Ь>с.

Тогда кубическое уравнение (4,1) вырождается в квадратное:

(4J)

= 1,

■ х² + у²,

с двумя корнями, пробегающими зна­чения в интервалах

1>

Координатные поверхности постоян- Рис. 8. ных £ и т] превращаются соответст-

венно в софокусные сплюснутые эл­липсоиды вращения и однополостные гиперболоиды вращения (рис. 8). В качестве третьей координаты можно ввести полярный угол ср в плоскости ху (x = pcoscp, */ = psin<p). Что же касает­ся эллипсоидальной координаты t, то при а = Ь она вырождает­ся в постоянную — а². Ее связь с углом ср заключена в законе, по которому £ стремится к —а², когда b стремится к а:

cos ср

(4.8)

ПРОВОДЯЩИЙ эллипсоид

39

в чем легко убедиться из (4,4) или непосредственно из уравне­ния (4,1). Связь координат z, р с координатами |, т] дается со­гласно (4,4) равенствами

(g + C²) (Г)+С²)

1/2

(g + a²) (г, + а²) a²—с²

1/2

(4,9)

Координаты |, г), ср называют сплюснутыми сфероидальными координатами ¹).

г/² + г²,

(4,10)

1,

Аналогичным образом, при a>fr = c эллипсоидальные коор­динаты вырождаются в так называемые вытянутые сфероидаль­ные координаты. Две координаты | и £ задаются корнями урав­нения

у2 _п2

,2

_а2_{+ и}-Г_Ь2

причем |^—Ь², —Ь²^3=£^ — а²- Поверхности постоянных £ и£ представляют собой вытянутые эллипсоиды и двухполостные гиперболоиды вращения (рис. 9). Коор­дината же т] вырождается при с —*- Ь в постоянную —Ь² по закону

coscp-]/^, (4,11)

где ср—полярный угол в плоскости yz.

Связь координат |, £ с координата­ми х, р дается формулами

(1+а²) (S + а²) а²— &²

(g + й²) (g + fc²)i б²—а²

7,

(4,12)

В сплюснутой сфероидальной системе фокусы координатных поверхностей (эллипсоидов и гиперболоидов) лежат на окружности радиуса Ya²—с² в плоскости ху (на рис. 8 А А' есть диаметр этой окружности). Проведем плоскость, проходящую через неко­торую точку Р и ось z. Она пересечет фокальную окружность в'двух точках; пусть г₁ и г₂—расстояния от этих точек до точки Р. Если р, z—координаты точки Р, то

r² = (p—/aⁱ^c²)² + z², r\ = (р + Va²^?)² + z².

Сфероидальные координаты ц выражаются через г_и г₂ по сле­дующим формулам:

*) Мы принимаем здесь такое определение сфероидальных координат, при котором они. являются предельным случаем эллипсоидальных. В литературе пользуютея и другими определениями, легко сводящимися к нашему.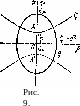

В вытянутой же сфероидальной системе фокусами являются две точки х — +У'а²—Ь² на оси х (точки А, А' на рис. 9). Если ^ri> ^г2 — расстояния от этих фокусов до точки Р, то

_г² = р² + (х_ ]/а²—&²)², г² = р² + (^ + ]/а²^Ь²)²,

а сфероидальные координаты £, £ выражаются через r_lt г₂ по тем же формулам (4,13) (с заменой г| на £).

Вернемся к задаче о поле заряженного эллипсоида, поверх­ность которого задана уравнением (4,3). В эллипсоидальных координатах это — координатная поверхность £ = 0. Поэтому ясно, что если искать потенциал поля в виде функции только от £, то автоматически будут эквипотенциальными все эллипсоидаль­ные поверхности | = const, в том числе поверхность проводника. Уравнение Лапласа (4,6) сводится тогда к уравнению

откуда

Верхний предел интегрирования выбран таким образом, чтобы обеспечить исчезновение поля на бесконечности. Постоянную А проще всего определить из условия, что на больших расстояниях г поле должно стремиться к кулоновскому: ср « е/r, где е—пол­ный заряд проводника. Стремлению г —>- оо соответствует ► оо; при этом г?«I, как это следует из уравнения (4,1) с ы = £. С другой стороны, для больших Е имеем R§ х £³/² и cp fS2A/Y% = = 2Л/г. Отсюда заключаем, что 2А=е, так что окончательно получим

<P(5) = fIf- (4,14)

Стоящий здесь интеграл — эллиптический первого рода. Поверх­ности проводника соответствует значение £ = 0, поэтому для емкости эллипсоида имеем

о

Распределение плотности заряда по поверхности эллипсоида определяется нормальной производной потенциала

С помощью уравнений (4,4) легко убедиться в том, что при £ = О

£_ , Ф_ , 2^ _ чС _л4 Т" (,4

Ь^{4 1} С⁴ 0²Й²С³ '

Поэтому

^СТ=4я^(-^ + |г + -] • (4,16)

Для двухосного эллипсоида интегралы (4,14) и (4,15) выра­жаются через элементарные функции. Для вытянутого эллипсоида (а>Ь = с) потенциал поля дается формулой

а его емкость

Для сплюснутого же эллипсоида (a = fr>c) имеем

, ⁶ arctg т/^=4-², С = ^Tfv- (4,19)

rA_a2__c2 ^& г ? + с² ' arrxos (с/а) ' '

В частности, для круглого диска (а = Ь, с = 0)

С = 2аЩ. (4,20)

Перейдем к задаче о незаряженном проводящем эллипсоиде, находящемся во внешнем однородном электрическом поле (£. Без ограничения общности достаточно рассмотреть внешнее поле ($, направленное вдоль одной из осей эллипсоида. В противном слу­чае можно разложить С- на три составляющие вдоль осей эллип­соида и искать результирующее поле как суперпозицию полей, получающихся от каждой из этих составляющих в отдель­ности.

Потенциал однородного поля ($, направленного вдоль оси х (ось а эллипсоида), в эллипсоидальных координатах имеет вид

Ф„ = —&х = —О?

(b¹ — а-) (с²—a²)

(4,21)

Представим потенциал поля вне эллипсоида в виде ф = ф₀ + ф', где ф' определяет искомое искажение внешнего поля эллипсоидом, и будем искать _Ф' в виде

_Ф' = ф/(|). (4,22)

В функции ф' зависящие от т) и £, множители совпадают с та­ковыми в ф₀; такой вид функции позволит удовлетворить гра­ничному условию при £ = 0 и произвольных г), t, (на поверхности эллипсоида). Подставив (4,22) в уравнение Лапласа (4,6), получим для F(|) уравнение

■ЩГ+-ЗГ 3i^InW5 + ^fle>] = o.

Одно из решений этого уравнения есть F = const, а другое имеет вид

i ^s

Верхний предел интегрирования выбран так, чтобы на бесконеч­ности (!—*оо) потенциал ср' стремился к нулю. Стоящий здесь интеграл — эллиптический второго рода.

На поверхности эллипсоида должно быть ср = const. Чтобы это условие могло выполняться при 1=0 и произвольных Г), £, надо положить const =0. Выбирая соответствующим образом ко­эффициент А в F (1) (так, чтобы было F (0) = — 1), получим окон­чательно следующее выражение для потенциала поля вокруг эл­липсоида:

£ СО CD ч

'^•j^lTi+re/lli+^T • ⁽⁴'²⁴⁾

Р ds

^{Найдем вид потенциала ср' на больших расстояниях г от эл­липсоида. Большим г соответствуют большие значения коорди­наты £, причем г2« £, как это следует непосредственно из урав­нения (4,1). Поэтому}

со со

Г ds Г ds 2

Ф

J (s + a²)/?₅ J s⁶'² За³-и для потенциала ср' получаем

<$,х V

г³ 4лп^(л:)

где У = 4яаЬс/3—объем эллипсоида, а величина п^{х) и аналогич­ные фигурирующие ниже величины п^{у\ п^и) определяются фор­мулами

00 СО 00

_(х) abc Г ds abc С ds afec р ds

^аЬс Г ^ds „(у) . Г» ds „(z>_^£f.

~ 2 J (s + a²)fl₅ ' ⁿ 2 J (s + 6²)^,' ⁿ ~ 2 J (s + c²)/?₅-

0 0 0

(4,25)

Выражение для cp', как и должно быть, имеет вид потенциала поля электрического диполя: причем дипольныи момент эллипсоида

Аналогичными выражениями определяются дипольные моменты при поле (S, направленном вдоль оси у или z.

Положительные постоянные п^ш, п^{у\ п^и) зависят только от формы эллипсоида, но не от его объема; они называются коэф­фициентами деполяризации ^J). Если не предрешать выбор осей координат вдоль осей эллипсоида, то формулу (4,26) надо пи­сать в тензорном виде:

fn_ik9>_k = %. (4,27)

Величины п^{х), п^{у\ n^w являются главными значениями симмет­ричного тензора второго ранга n_lk. Сравнение с определением (2,13) показывает, что a_ik = n~^/in есть тензор поляризуемости проводящего эллипсоида.

В общем случае произвольных значений а, Ь, с из опреде­лений n^ix), п⁽у\ п^{г) следует прежде всего, что

_пш <• _п(_У) <• _пи>_{( если} а>Ь>с. (4,28)

Далее, сложив интегралы п^{х), п^{у\ п^{г) и введя в качестве пе­ременной интегрирования u=R\, найдем

² J_c)y

откуда

n⁽*> +я^> + п<" = 1. (4,29)

Сумма трех коэффициентов деполяризации равна единице (в тен­зорном виде это значит, что п_п = 1). Поскольку, с другой сто­роны, эти коэффициенты положительны, каждый из них не мо­жет превышать единицы.

Для шара (а = Ь=с) из соображений симметрии ясно, что

Для цилиндра (с осью вдоль оси х, а —* оо) имеем ?)

*) Эти же коэффициенты фигурируют в задачах о диэлектрическом эл­липсоиде во внешнем электрическом поле или магнитном эллипсоиде в маг­нитном поле (§ 8). Таблицы и графики этих коэффициентов для эллипсоидов вращения и для трехосных эллипсоидов можно найти в статьях: Stoner Е. С.— Phil. Mag., 1945, v. 36, p. 803; Osborn J. A. — Phys. Rev., 1945, v. 67, p. 351.

²) Эти значения для шара и цилиндра находятся, разумеется, в соответст­вии с результатами, полученными в задачах 1 и 2 § 3.

«⁽*>=0, п<^ = п^(г) = 7₂- (4,31)

Предельному же случаю a, b —* оо (плоская пластинка) отвечают очевидные значения

п^м^-11^=0, п^(г> = 1.

Эллиптические интегралы (4,25) выражаются через элементар­ные функции для всех эллипсоидов вращения. Для вытянутого эллипсоида вращения (а>Ь=с)с эксцентриситетом e=V^l—Ь²/а² имеем

n<*>=i=^²(Arth е—е), я⁽^=п^(г) = ¹/₂ (1 —п^(ж))- (⁴-³²) Если эллипсоид близок к шару (е<^1), то приближенно

«^U)=V₃-²/₁₅e², tt^ = tt⁽*> = V₃ + V₁₅e². (4,33)

Для сплюснутого же эллипсоида (а = Ь>с):

_nt« = i±£! (е_arctge), n⁽^> = V₂ (1—«⁽²⁾), (4,34)

где е = }/а²/с²—1. Если е<^1, то

"^^Va + Vue², п⁽«=п^^¹/з-¹/_1вг*. (4,35)

Задачи

1. Найти поле заряженного проводящего круглого диска (радиуса а), вы­разив его в цилиндрических координатах. Найти распределение заряда на диске.

Решение. Распределение ?аряда получается путем перехода в формуле (4,16) к пределу с—»■ 0, г—>■ 0, причем отношение г/с=У~1 — г²/а² (где

/

а =

-х²-\-у²) в соответствии с (4,3). Это дает е /' г² \ -¹ /²

4яа²

^{1—^-}

а²

Потенциал поля во всем пространстве опреде­ляется (4,19), в которой полагаем с — 0 и выра­жаем \ через гиге помощью уравнения (4,1) при с = 0, « = £, а = Ь:

-X

Рис. 10.

, Г 2а²

XarCtg ^_r2_+z2__a2₊[(_r2_+z2__Q2₎2₊4_a2_z2jl ,2

Вблизи края диска вводим вместо г и г координаты р и 9 согласно г = р sin 9, r = a—pcos9 (p<^a) (рис. 10) и находим

в согласии с общим результатом задачи 3 § 3.

2. Определить квадрупольный электрический момент заряженного эллип­соида.

Решение. Тензор квадрупольного момента заряженного проводника оп­ределяется как = ^е i^^xi^xk — '■²°!'fe). ^гД^{е е}—^его полный заряд, а черта озна­чает усреднение по закону

*i*k = ~ <§ ^х'^хк^{а d}f-

Очевидно, что оси эллипсоида являются в то же время главными осями тен­зора £>,•£. Воспользовавшись для а формулой (4,16), а для элемента поверх­ности эллипсоида выражением

dx dy dx dy

v_z ~~ z/c²

+-Й-+-

1,2

(v—единичный вектор нормали к поверхности эллипсоида), получим

Г с²

АлаЬ

(интегрирование по dx dy производится дважды по площади сечения эллип­соида плоскостью ху). Таким образом,

D_xx = ^(2a²-b²-c²), />„„ = -=-(2&^а-а^а-с*)

D_zz = -(2c²-a²-b²).

3. Найти распределение зарядов на поверхности незаряженного проводя­щего эллипсоида во внешнем однородном поле. Решение. Согласно формуле (1,9) имеем

1 дц, 4я дп

1=0

1

4я/г_х д£ /| = о

(элемент длины вдоль направления нормали к поверхности эллипсоида есть согласно (4,5) h-^%). С помощью (4,24) и учитывая, что

_ ' дх х

получим

0=®

4лп^{х)'

При произвольном направлении внешнего поля относительно осей х, у, г эллипсоида

М- к

g.

4. То же для незаряженного круглого плоского диска (радиуса а), рас­положенного параллельно полю Определить дипольный момент диска.

Решение. Рассматриваем диск как предел эллипсоида вращения при стремлении полуоси с к нулю. При этом коэффициент деполяризации вдоль этой оси (ось z) стремится к 1, а вдоль осей х и у—к нулю по закону

п«> =!—££, _п<*> = 2а

=п<у>==£,

4а

*) Для диска, расположенного перпендикулярно к полю, вопрос был бы тривиален; поле остается однородным во всем пространстве, а на двух сторо­нах диска индуцируются заряды а=±@/4я.

следующему из (4,34). Компонента v_x единичного вектора нормали к поверх­ности эллипсоида вращения стремится к нулю по закону

X (Х^Ъ-\-и^Ъ . 2²\-^li2 ХС^Ъ XC , ,

Поэтому плотность зарядов

g_(£ ^Vx ₌g ^pcos(P

4яя^(д;> л- у а¹ р² '

где р, ф—полярные координаты в плоскости диска.

Дипольный момент диска определяется по формуле (4,26) и равен

4 а³ ^ Зя

Отметим, что он пропорционален а³, а не «объему» диска а²с.

5. Определить потенциал поля вне незаряженного проводящего эллипсоида вращения, расположенного своей осью симметрии параллельно внешнему одно­родному полю.

Решение. Для вытянутого эллипсоида вращения (а>6 = с, поле 6 в направлении оси ж) получим, вычислив интеграл в формуле (4,24),

_{J, ^S^Sj}

Ф=_е* !- _f—_ .—_ у.

Координата % связана с координатами х и р=Уг/² + г² посредством

причем в пространстве вне эллипсоида (KgsSoo.

Для сплюснутого эллипсоида (а = Ь > с) поле 6 направлено вдоль оси г. В связи с этим в интегралах в (4,24) надо заменить s-fa² на s-f-c² и взять ф₀=—Qz. В результате получим

т+г-"^гс,г У т-

причем координата | связана с координатами z и р—Ух^-^-у² посредством

Р² I z³ __л

_fl2 ₊ g-T_c2+g

6. То же, если ось симметрии эллипсоида перпендикулярна к внешнему полю.

Решение. Для вытянутого эллипсоида (поле в направлении оси г):

Для сплюснутого эллипсоида (поле в направлении оси х):

1

arctg

~² Vl+c-

-Q,x

:tg j/j-¹--^

7. Однородное поле (S, направленное вдоль оси г (в полупространстве г < 0), ограничено заземленной проводящей плоскостью г = 0 с круглым отвер­стием. Определить поле и распределение зарядов на плоскости.

Решение. Плоскость ху с круглым отверстием радиуса а с центром в начале координат рассматриваем как предельный случай однополостного ги­перболоида вращения

Р-

|Г)|

hi

при | г) | —у 0. Эти гиперболоиды представляют собой одно из семейств коор­динатных поверхностей сплюснутой сфероидальной системы координат с с = 0. Декартова координата г выражается согласно (4,9) через | и г| посредством г= ]/"Е | г) |/а, причем корень ]/"| должен быть взят со знаком+или— соот­ветственно в верхнем и нижнем полупространствах.

Ищем решение в виде ф=— F (Q и для функции F (Е) получаем

F(E) =const­

_jV²

(E + fl^a)

: COnSt •

a , a

—= —arctg ——

Vl Vl

(постоянную интегрирования полагаем равной нулю в соответствии с условием ф = 0 при г—^+оо, т. е. при ~]f\—>--|_оо). При этом arctg отрицательного аргумента надо понимать как

, а а

arctg ==л—arctg —— ,

-Vl Vl

а не как — arctg (a/Vl). В противном случае потенциал испытывал бы разрыв непрерывности на плоскости отверстия (£ = 0). Постоянный коэффициент вы­бираем так, чтобы при г—► — оо (т. е. при VI—► — оо, arctg (a/Vl)—*л) было ф=—(?2, и окончательно получаем

Vl

/с ² Г i ^{а а} ф= —© — arctg —= —

^п [ Vl Vl.

VU\

■arctg

V Е ^а

1

На проводящей поверхности т) = 0 и потенциал, как и следовало, обращается в нуль.

На больших расстояниях r= V^z~-rP~ °т отверстия имеем Е я г- и потен­циал (в верхнем полупространстве) приобретает вид

ф^ е

а¹ V — Ц Зл~ Е

Злг³

т. е. поле—дипольного типа, соответствующее дипольному моменту Ф — = 6а³/3л.

Напряженность поля убывает как г^-3, и потому ноток поля через беско­нечно удаленную поверхность (в полупространстве г > 0) обращается в нуль. Это значит, что все силовые линии, проходящие через отверстие, замыкаются на верхней стороне проводящей плоскости.

Распределение зарядов на проводящей плоскости вычисляется следующим образом:

-г 1 дф 4л dz

г=0 4л J^g й — т) ^4я"

^arctg7T FFJ

где верхние н нижние знаки относятся к верхней н нижней сторонам пло­скости. Согласно формуле

^р2 4-4=1.

связывающей g с р, z, на плоскости z = 0 имеем /| = ± Ур² — о². Таким образом, распределение зарядов на нижней стороне проводящей плоскости дается формулой

1 / . а . а

При р—>- оо имеем а=—К/4л, как и должно быть. На верхней же стороне

,_ 1 / а .а

а=— ©т—;[ —= — arcsin —

Ы-\у_р>__а2 р

Полный индуцированный заряд на верхней стороне плоскости конечен и равен

со

е'= \ a-2npdp = —g.

8. То же, если отверстие в проводящей плоскости представляет собой прямую щель ширины 26.

Решение. Плоскость ху со щелью вдоль оси х рассматриваем как пре­дельный случай гиперболического цилиндра

У"¹ z²__j

Ъ- — |т)| |гц

при | т) |—>. 0. Эти гиперболические цилиндры представляют собой одно из семейств эллипсоидальных координатных поверхностей при а—»-оо, с—»■ 0. Декартова координата г = у g | т)

Как и в задаче 7, ищем решение в виде ф=—(5zF(g) и для функции f (g) получаем

F-- const ■

Здесь коэффициент и постоянная интегрирования определяются условиями F — О и F = 1, соответственно, при z -*--|- оо иг-» — оо (т.е. при ]/" g ->- -)- оо и ]/" |-»-—оо), и окончательно получаем

^{ф - е ^ [ VIW2 т VI]Vm>}

где мы теперь понимаем корень У g как положительную величину, а верх­ний и нижний знаки соответствуют областям г > 0 и г < 0.

На больших расстояниях от щели в верхнем полупространстве имеем g « г/² + г² =г² и потенциал

^{ф,4/^}₌

^И 4г² '

т.е. поле двумерного дипольного типа с дипольиым моментом К-6²/8 на еди­ницу длины щели (см. формулу в задаче 2 § 3).

Распределение зарядов на проводящей плоскости дается формулой

8яДт/у_₆2 )

Полный индуцированный заряд на верхней стороне плоскости (отнесенный к единице длины щели) равен

00

Вблизи края щели в выражении для ф(Е, т)) можно положить £ -»■ 0 и т) я —26р sin² -у,

где р, 9—полярные координаты в плоскости уг, отсчитываемые от края щели (j/ = 6 + pcos9, 2 = psin9). Тогда

~ -, /"bp . 9

ф ~ © ]/ у ^sm"2 •

в согласии с результатом задачи 3 § 3 для случая 6₀<^1.