!) Более точная формула, п= 1/(2 In (2/9₀)), содержащая коэффициент в большом логарифме, в действительности не может быть получена указанным простым методом. Более точное вычисление, однако, по случайным причинам приводит именно к этой формуле.

²) Аналогичная задача для двух сфер не решается в конечном виде. Раз­ница связана с тем, что в поле двух заряженных (равными н противополож­ными зарядами) параллельных нитей все эквипотенциальные поверхности являются круговыми цилиндрами, а в поле двух точечных зарядов ± е экви­потенциальные поверхности не являются сферами.

2 Л. Д. Ландау, е. М. Лифшиц

7. Определить взаимную емкость единицы длины двух параллельных бес- конечных цилиндрических проводников (радиусов а и Ь, расстояние между осями с) ²).

Решение. Поле, создаваемое обоими цилиндрами, совпадает с полем, которое создавалось бы (в пространстве вне цилиндров) двумя заряженными нитями, проходящими через соответствующим образом подобранные точки А и А' (рис. 4). Нити несут (на единице длины) заряды ± е, равные зарядам цилиндров, а точки Л и Л' должны быть расположены на линии 00' так, чтобы поверхности цилиндров совпадали с эквипотенциальными поверхностями.

Для этого расстояния OA и О'А' долж­ны удовлетворять соотношениям

О А-О А'= а?, 0'А'-0'А = Ь^г,

т. е.

dj(c — d₂) = a², rf₂(c—dj) = 6².

Тогда на каждой из окружностей отно­шение г'/г расстояний от точек А и А' постоянно: на окружности /

0'A'=tf_z ^и г _ а а _ d₁

р_ис 4 г' OA' ~c — d₂~~ а

а на окружности 2 r'Jr — d₂/b. Соответственно, потенциалы цилиндров:

г d, „ , d„ „ , d-tdn

q>i = - 2eln-p- = — 2e\n-^ , q>₂ = 2eln-^-, ф₂ — ф_{1 =} 2« In .

Отсюда находим для искомой взаимной емкости С = г/(ф₂ — ф_х):

-7г=2 п -V=2 Arch ₀—г •

С ab 2аЬ

В частности, для цилиндра радиуса а, находящегося на расстоянии h > а от проводящей плоскости, надо положить c=b-^s_rh и перейти к пределу b—<-оо;

это дает

-^ = 2 Arch А. С а

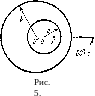Если два полых цилиндра находятся один внутри другого (с < Ь-поле снаружи отсутствует, а поле в пространстве между цилиндрами дает с полем, которое создавалось бы дву­мя нитями с зарядами -\-е и —е, прохо­дящими через точки А а А' (рис. 5). Тем же способом получим результат:

2ab

-^г = 2 Arch —

8. Граница проводника представляет собой неограниченную плоскость с высту­пом в виде полушария. Найти распределе­ние зарядов на поверхности.

Решение. В найденном в задаче 1 поле с потенциалом вида

/ R³ Ф= const -г II з~

-а), то совпа-

плоскость г = 0 с выступом r=R является эквипотенциальной поверхностью (на которой ф = 0). Поэтому она может быть и поверхностью проводника, а написанная формула определяет поле вне проводника. Распределение

зарядов на плоской части поверхности дается формулой

_1_ Лр 4я dz

г=о

(мы положили const = —4яа₀, где а₀ — плотность зарядов вдали от выступа). На поверхности же выступа

„_ 1 дц.

An дг

9. Определить дипольный момент тонкого проводящего цилиндрического стержня (длины 21, радиуса а; а<^1) в электрическом поле (J, параллельном его оси.

7i

х (z') dz' Ар

Решение. Пусть х (z)— индуцированный на поверхности стержня заряд, отнесенный к единице длины; z—координата вдоль оси цилиндра, которую будем отсчитывать от его середины. Условие постоянства потенциала на по­верхности проводника гласит:

= 0, R =

2я 1

(г'— z)² + 4а² sin²-|-

(ф — У^гол между плоскостями, проходящими через ось цилиндра и через точки на его поверхности, расстояние между которыми равное). Разобьем интеграл на две части, написав в нем тождественно т (г') =т (г) + [х (г')—т(г)]. Учи­тывая, что 1^>а, и рассматривая точки, не слишком близкие к концам стержня, имеем

х (z) С С dz'dw х (z)²?. /²—z² , 4 (/² —z²)

о

^использовано известное значение ^ In sin ф d<p=— я In 2 J. В интеграле, со­держащем разность т(г')—т(г), можно пренебречь членом с а' в ^, так как это не повлечет за собой расходимости интеграла. Таким образом,

(£z = t (z) In

4 (/²—z²)

Т(2')— X(Z)

dz'.

Зависимость x от z в основном сводится к пропорциональности z; в этом при­ближении стоящий здесь интеграл дает —2т (z), и в результате получаем

@2

⁽²⁾ In [4(/²—z²)/a²] —2^-

Это выражение непригодно вблизи концов стержня, но для вычисления иско­мого дипольного момента эта область значений z несущественна. С принятой нами здесь точностью имеем:

² i Л ²

5» = j T(z)zdz=|- J о

(где L=ln(2//a)— 1—большое число), или, с той же точностью,

@/³

-1п2

3[In(4//a)-'/₃] *

- Г²/г' (I — длина

10. Определить емкость полого сферического проводящего сегмента. Решение. Выберем начало координат О в какой-либо точке края сег-

мента (рис. 6) и произведем преобразование инверсии

хорды в главном сечении сегмента). При этом сегмент переходит в полупло­скость (штриховая прямая на рис. 6), перпендикулярную к радиусу АО сег­мента и проходящую через точку В его края; угол у = л — 6, где 2G — угол раство­ра сегмента.

ф=

Если потенциал сегмента, несущего на себе заряд е, принчть за нуль, то при г —>■ со потенциал поля стремится к

-фо-

.!ф»-|_

г' '

Соответственно, в преобразованной задаче при г'—*• 0 потенциал стремится к , /го /ф„ , е ф =J

I

(первый член соответствует заряду е' = —/ф₀ С другой стороны, согласно (3,22) имеем

, е|_ /' , 0

^ф г' 2л/I ⁺s.n0

в начале координат).

(потенциал вблизи заряда е', находящегося на расстоянии / от края проводя­щей полуплоскости с потенциалом нуль). Сравнив оба выражения, получим для искомой емкости С = е/ф„ следующую формулу:

2л V

1 +

Sin I

= —■ (s;n

6 + 6)

(R— радиус сегмента).

П. Определить связанную с краевыми эффектами поправку к значению C=S/4nd для емкости плоского конденсатора (S — площадь поверхности об­кладки, d—расстояние между обкладками; d<^]fS).

а) 4

— tp=0

б)

Решение. Наличие у обкладок свободных краев нарушает равномерность распределения зарядов на них. Для определения искомой поправки в первом приближении рассматриваем точки об­кладок, удаленные от края на расстоя­ния х такие, что d<^x<^]/^S. Рассмат­ривая, например, верхнюю обкладку (с потенциалом ф = ф₀,<2; рис. 7, а) и пренебрегая ее расстоянием rf/2 до сред­ней плоскости (эквипотенциальная по­верхность ф = 0), мы получаем задачу о поле вблизи границы двух частей плос­кости, имеющих различные потенциалы (рис. 7, б). Эта задача решается элемен­тарно ³), и в результате для избыточной (по сравнению с а вдали от края) плот­ности зарядов получается выражение

4л

, ^Еп _ фо

Дсг=

^х) См. § 23; в формуле' (23,2) для потенциала надо положить в данном случае ф_аь = фо/2, а = л.

так что полный избыточный заряд

(L—длина периметра обкладки); при вычислении логарифмически расходяще­гося интеграла в качестве верхнего и нижнего пределов подставляем границы области d <^ х <^ У S.

Отсюда находим емкость:

_г__ S L y~S

Более точное вычисление (определение коэффициента в аргументе лога­рифма) требует применения значительно более сложных методов, причем ре­зультат зависит от формы обкладок. Для круговых (радиуса R) обкладок получается

(формула Кирхгофа).