37

Лекційно – практичний посібник з функціонального аналізу

Зміст

Лекція 2. Скалярний добуток. Гільбертовий простір. Ортонормований базис. Простір Фока. 5

Практичне заняття 1. Банахови та гільбертові простори. 8

Лекція 3. Лінійний неперервний функціонал. Загальний вигляд лінійного неперервного функціонала у гільбертовому просторі. 10

Лекція 4. Узагальнені функції. Узагальнені функції повільного росту. 11

Практичне заняття 2. Лінійний обмежений функціонал. Узагальнені функції. 13

Лекція 5. Лінійний неперервний оператор у банаховому просторі. Добуток. Обернений оператор. 15

Лекція 6. Лінійні неперервні оператори у гільбертовому просторі. 18

Лекція 7. Матричне представлення операторів. Оператори Гільберта – Шмідта 19

Практичне заняття №3. Лінійний обмежений оператор. Оператори у гільбертовому просторі. 21

Лекція 8. Спектр і резольвента оператора. Функції від операторів. 23

Лекція 9. Означення та властивості компактних операторів. Приклади. 24

Практичне заняття 4. Спектр, резольвента. Компактні оператори. 25

Лекція 10. Альтернативи Фредгольма. Інтегральні рівняння Фредгольма. 26

Практичне заняття 5. Рівняння Фредгольма. 27

Лекція 11. Спектральний розклад компактного самоспряженого оператора. 29

Лекція 12. Розклад одиниці. Спектральні інтеграли та спектральний розклад обмеженого самоспряженого оператора. 31

Лекція 13. Елементи теорії необмежених операторів. Фізична інтерпретація. Еволюційні рівняння. 32

Практичне заняття 6. Розклад одиниці. Спектральний інтеграл та спектральне представлення самоспряженого оператора. 35

Література 36

Передмова

Даний посібник розраховано на студентів фізико – математичного факультету зі спеціальності «Математика» денної та заочної форми навчання.

Не зважаючи на те, що матеріал посібника викладено у скороченому вигляді він повністю відповідає навчальній програмі. Лекційну частину можна розглядати як теоретичний довідник, необхідний для розв’язування задач, що пропонуються у практичних заняттях. Відмітемо, що частково теоретичний матеріал винесено у задачі.

Для більш глибокого вивчення матеріалу можна запропонувати літературу, яка приведена в кінці посібника.

Ми маємо надію, що не зважаючи на стислість, посібник все ж допоможе студентам отримати уявлення про функціональний аналіз та його застосування, а також зв’язок з іншими розділами математики.

Лекція 1. Означення норми. Нормовані та счисленно – нормовані простори. Приклади.

1. Означення норми.

Означення. Нехай Е – лінійний простір. Числову функцію називають нормою, якщо вона задовольняє властивостям:

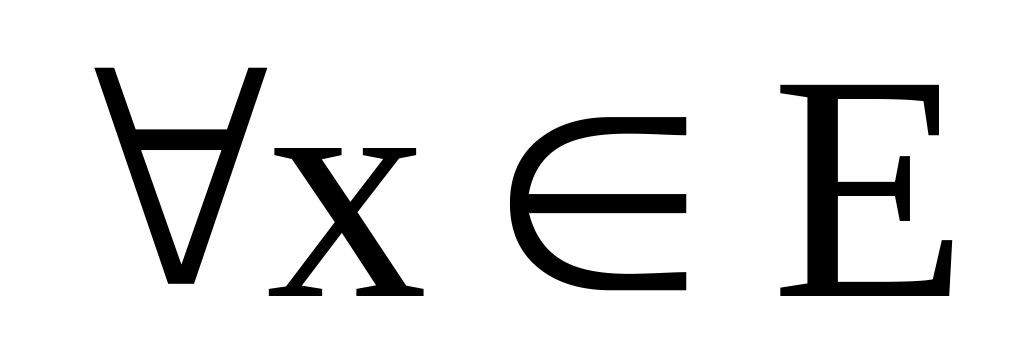
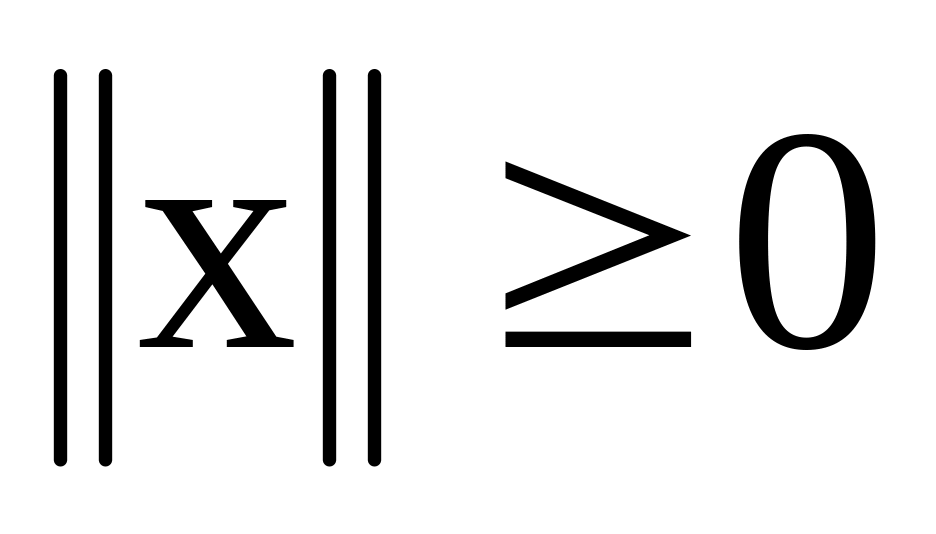1. , причому 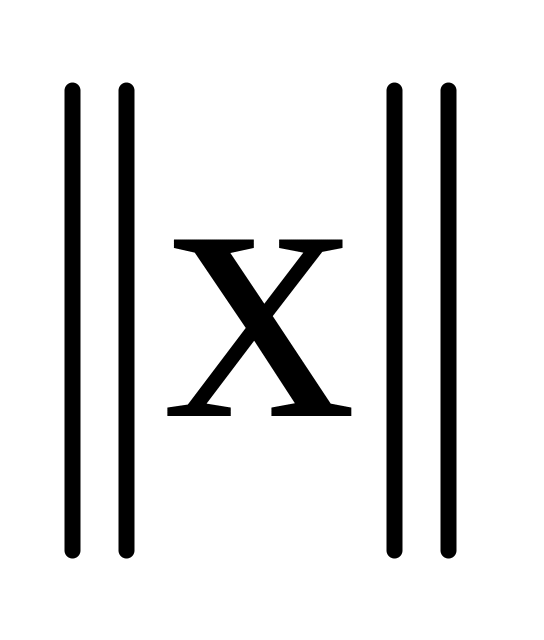= 0 ↔ х = 0.

2. .

3. .

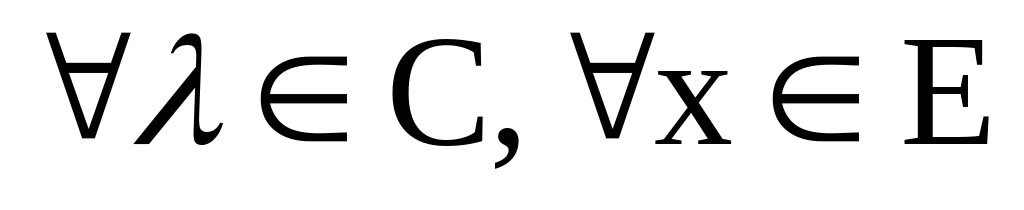
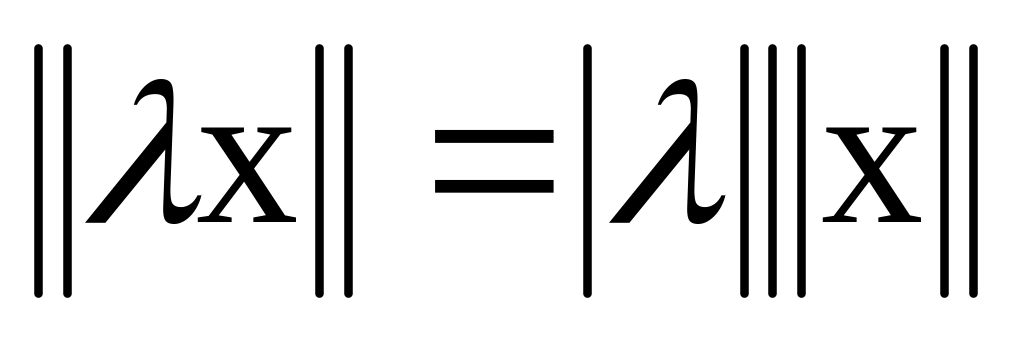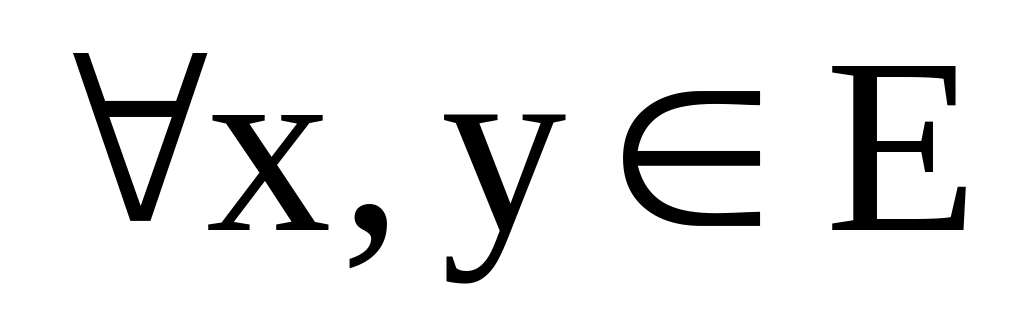
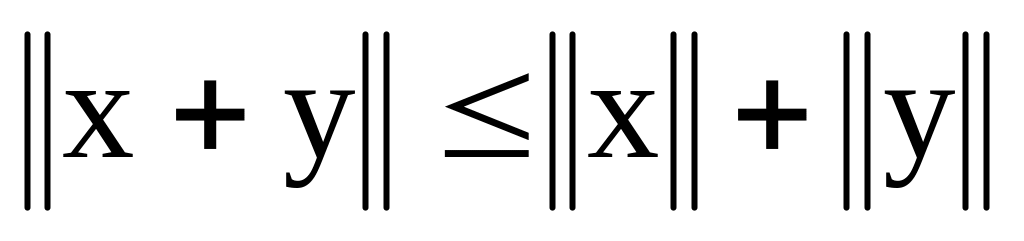З означення легко довести, що:

1.

2. (довести самостійно).

Означення. Лінійний простір Е, в якому задана норма, називають нормованим простором.

Приклади.

1. .

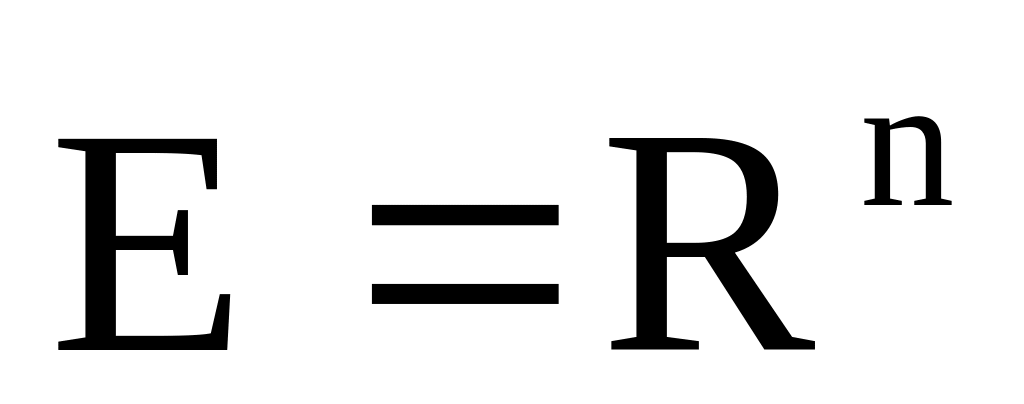
2. Е = С [a, b] .

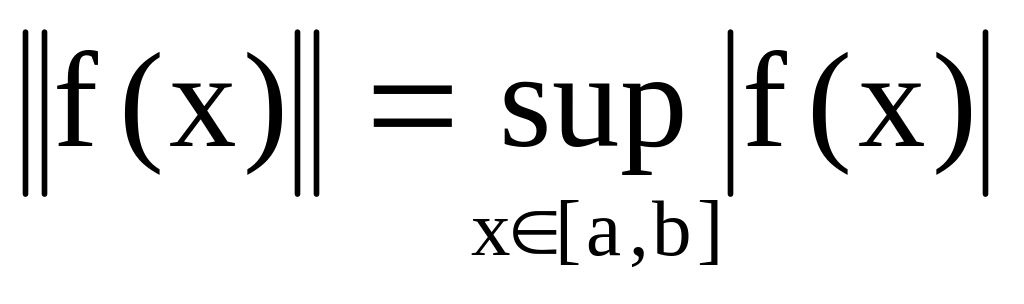3. Е =

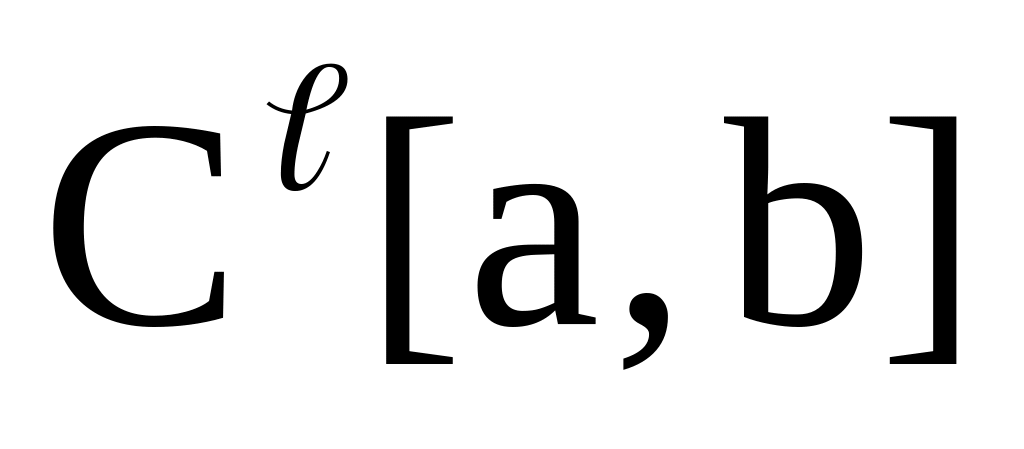
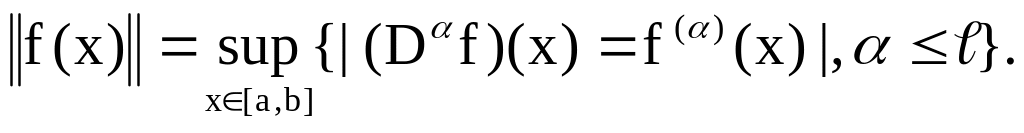
4. E = 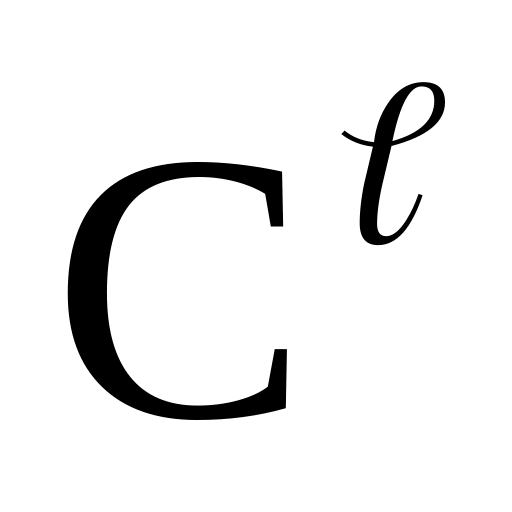(G) – простір l – раз неперервно – диференційованих функцій (G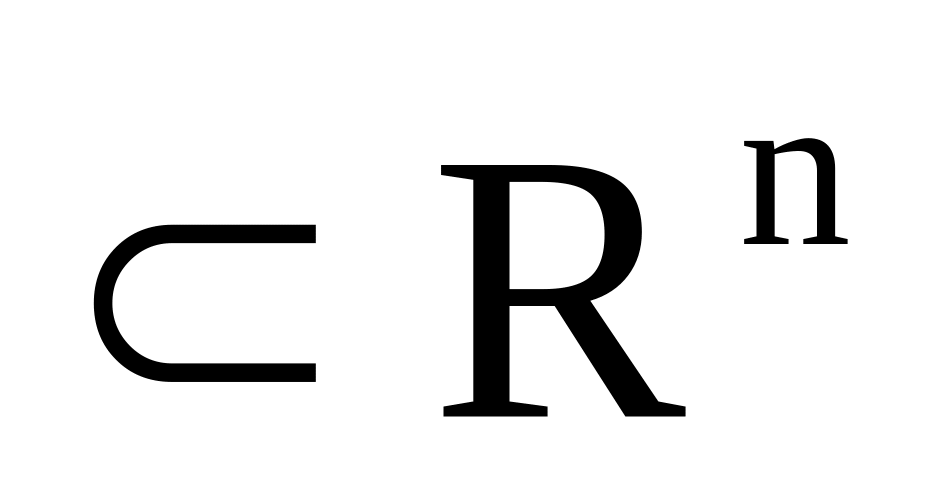 , обмежена та замкнена область) }

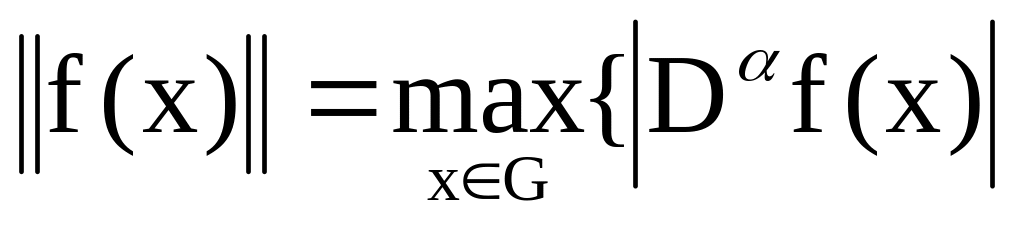
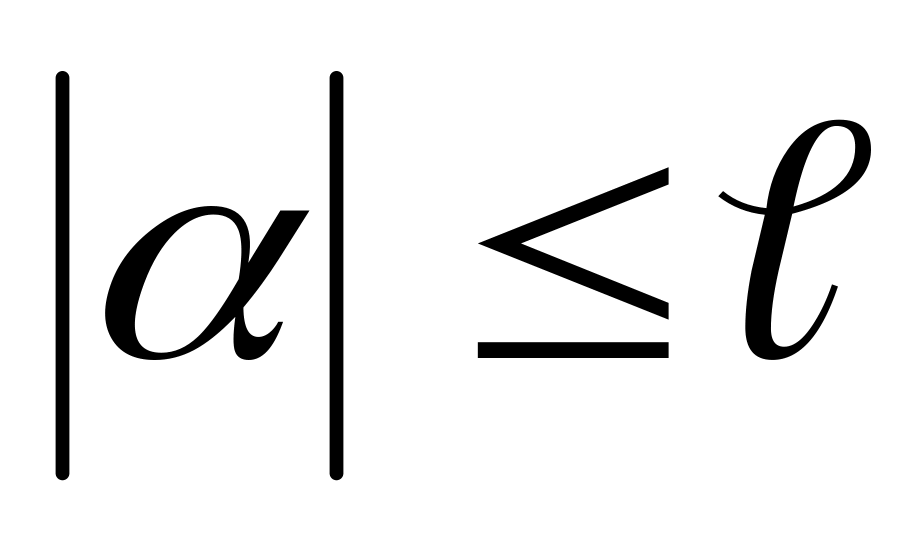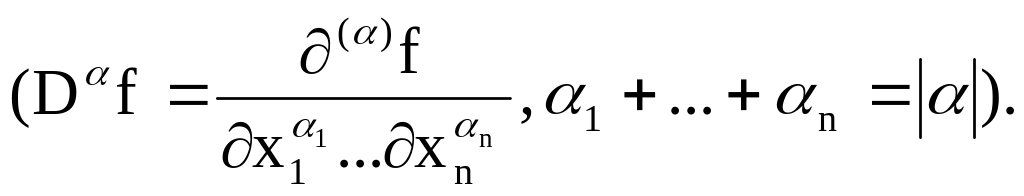
5. Нехай ( R, R, μ) довільний вимірний простір з мірою, тоді 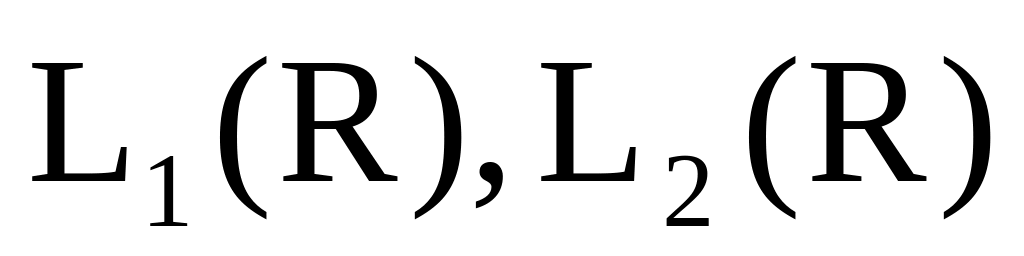нормовані простори з нормами ,

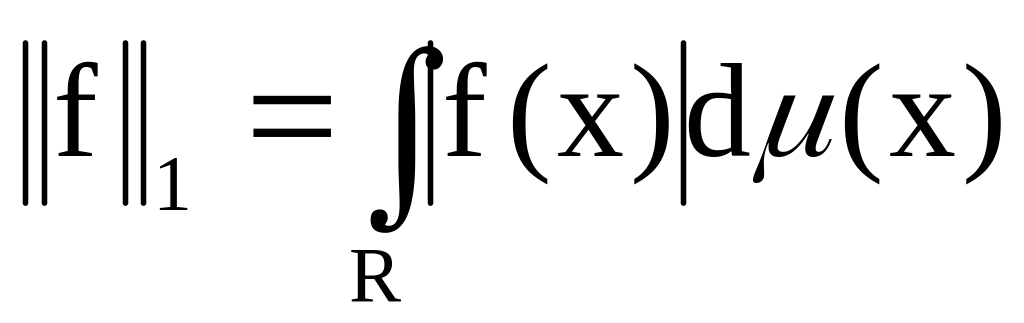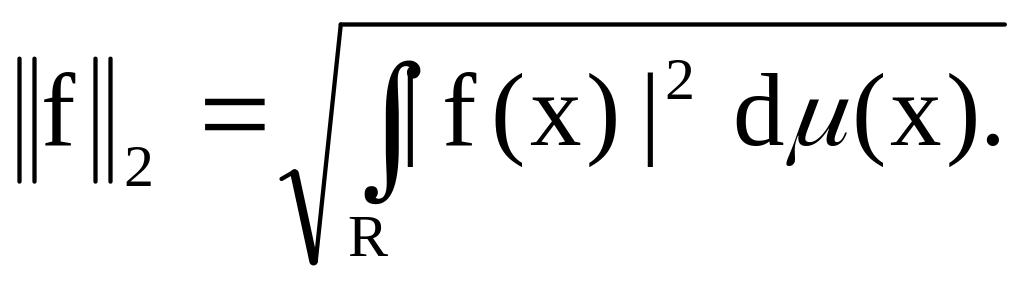
Якщо Е – лінійний нормований простір, то задовольняє аксіомам метрик ( перевірити самостійно ), отже Е – метричний простір, в якому визначено поняття границі послідовності. Тобто означає, що

Згадаємо, що послідовність називається фундаментальною, якщо , n, m > N . Якщо будь – яка фундаментальна послідовність у просторі має границю, то простір називають повним.

Означення. Повний лінійний нормований простір називають банаховим простором.

У прикладах 1 – 5 всі простори є банаховими.

З загальної теорії метричних просторів випливає теорема.

Теорема. Для будь – якого лінійного нормованого простора Е існує банаховий простір такий, що : 1. Е ; 2. ; 3. Е всюди щільно в .

Приклад. Нехай G – обмежена замкнена область у . (G) – простір l – раз неперервно диференційованих в G функцій ( приклад 4 ). Розглянемо норму на (G) (G),

Означення. Соболевським простором називають поповнення (G) по нормі