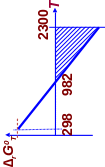
С (графит) 298 – 2300 к

СО₂ (г) 298 – 2500 К

СО (г) 298 – 2500 К Þ

Искомая область температур: 982 ÷ 2300 к

Лекция 11. Химическое равновесие

Состояние системы, при котором энтальпийный и энтропийный факторы уравновешиваются Þ ∆_r G_Т = 0

∆_r G_Т = ∆_r H_Т - T∆_r S_Т = 0 ∆_r H_Т = T∆_r S_Т

Þ возможности самопроизвольного протекания прямой и обратной реакции равновероятны Þ парциальные давления и концентрации всех компонентов реакции постоянны во времени и во всех точках системы - равновесные давления и концентрации.

При равновесии химической реакции:

aA_(г) + bB_(г)+ dD_(к)  eE_(г) + fF_(г)

Δ_r G_Т = ∆_r G⁰_Т + RTln = 0 Þ

! под знаком логарифма относительные равновесныедавления

∆ _r G⁰_Т = -– RTln

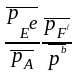
Если реакция aA _(р) + bB _(р)+ dD _{(к )}  eE _{(р )} + fF _(р) протекает в идеальном растворе:

∆_r G⁰_Т = – RTln

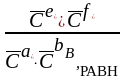
Математическое выражение закона действующих масс (ЗДМ) для равновесного состояния:

К_с =

К_р =

К_с и К_р - константы равновесия

∆_r G⁰_Т = - RTlnК_р для реакций в газовых системах (1)

∆_r G⁰_Т = - RTlnК_с - для реакций в конденсированных системах (1′)

К_р и К_с

• определяются природой веществ

• зависят от Т

не зависят от:

• парциальных давлений

• концентраций компонентов

• общего давления в системе

К_р и К_с - характеризуют выход продуктов реакции

Из уравнений (1), (1′) следует:

Δ_r G⁰_Т < 0,

если lnК_равн ˃ 0, т.е. К_равн ˃ 1 Þ равновесие смещено вправо

(в равновесной смеси больше продуктов)

Δ_r G⁰_Т ˃ 0,

если lnК_равн < 0, т.е. К_равн < 1 Þ равновесие смещено влево

(в равновесной смеси больше исходных веществ)

Соотношение К_р и К_с для газофазной реакции

Парциальные давления газов характеризуют их содержание в реакционной смеси и м. б. заменены на концентрации.

Для реакции:

aA_(г) + bB_(г)+ dD_(к)  eE_(г) + fF_(г)

К_р = =

=

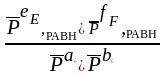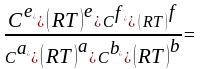
К_р = К_с(RT)^∆ν

∆ν = (e + f) – (a + b) – изменение числа молей газов в результате реакции

! R = 0,082 атм^.л^.моль^-1.К^-1

Выражение К_р - через равновесные количества молей газообразных компонентов n_{i (равн)} и общее давление P₀:

p_i = 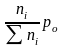- парциальное давление компонентов

Σn_i = n_{E равн} + n_{F равн} + n_{A равн} + n_{B равн}

К_р = =

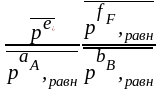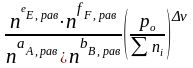
Зависимость константы равновесия от температуры

∆_r G⁰_Т = - RTlnК_р = ∆_r H⁰ - T∆_r S⁰

lnK_p = - = 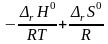, с учетом ∆_rH⁰ и ∆_rS⁰ ¹ f(T)

уравнение изобары Вант-Гоффа

если ∆_r H⁰ < 0 Þ d lnK_p/dT < 0 Þ К_р уменьшается с ↑ Т равновесие смещается влево, в сторону исходных веществ

если ∆_r H⁰ > 0 Þ d lnK_p/dT > 0 Þ К_р увеличивается с ↑ Травновесие смещается вправо, в сторону продуктов реакции

После интегрирования изобары с учетом ∆_r H⁰ ¹ f(T) при Т₂ > Т₁ :

Принцип Ле Шателье

если на систему, находящуюся в истинном равновесии, воздействовать извне, то равновесие смещается в сторону уменьшения эффекта внешнего воздействия

Равновесие смещается:

при ↑ Т Þ в сторону эндотермической реакции

при ↑ Р_общего Þ в сторону образования меньшего числа моль газообразных реагентов

при ↑ Р_{исходных веществ} Þ в сторону продуктов реакции

при ↑ С_{исходных веществ} или при ↓ С_{продуктов реакции} Þ в сторону продуктов

ЗАДАЧА

Рассчитайте К_р и К_с реакции

С_(к) + СО_2(г) 2СО_(г)

при 298 К и 1000 К. Сделайте вывод о выходе продукта реакции и определите знак энтальпии реакции.

Решение:

К_р = 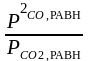; К_с =

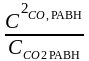
∆_r G⁰_Т = –RT lnК_р Þ K_p = exp(–∆G⁰_Т /RT)

∆_r G⁰₂₉₈ = 120,15 кДж; ∆_r G⁰₁₀₀₀ = –3,16 кДж

К_р298 = exp(–120 · 10³ / 8,31· 298) = ехр( –48,5) = 8 × 10^–22

K_p1000 = exp(+3160 / 8,31 · 1000) = ехр(0,38) = 1,46

(обратите внимание на размерность!)

К_с = 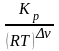= = 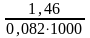0,018

∆ν = 2-1=1 - изменение числа молей газообразных веществ!

При 298 К: К_р ® 0 Þ в равновесной смеси практически отсутствуют продукты Þ смещение равновесия в сторону исходных веществ.

При 1000 К: К_р > 1 Þ в равновесной смеси начинают преобладать продукты, их выход растет с ↑ Т,с ↑ Т значение К_р увеличивается Þ ∆_r H⁰ > 0.

ЗАДАЧА

Определить равновесный состав системы

С(к) + СО₂(г) 2СО(г)

Т= 1000 К Р_общ = 2атм n_{исх, CO2} = 5 моль

Решение:

Реакция идет при P = const!

K_p =exp(- ∆G⁰_Т /RT)

K_p1000 = exp(+3160/8,31^.1000)= ехр(0,38) = 1, 46

Компонент	С	СО2	2СО
Начальный состав, моль	-	5	0
Изменение состава, моль	-	х	2 x
Равновесный состав, моль	-	5 – x	2 x

К_р = = =

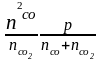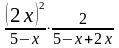= = 1,46 Þ х = 1,7 моль.

Равновесный: n(СО₂) = 5 - 1,7 = 3,3

состав: n(СО) = 2×1,7 = 3,4.

ЗАДАЧА

Определите с_равн СО₂ и СО для реакции

С(к) + СО₂(г) 2СО(г)

Т = 1000 К , V_сосудa = 2 л, m_исх (СО₂) = 44 г,

Рассчитайте, на сколько изменится давление в системе при равновесии по сравнению с исходным

Решение:

Реакция идет при V = const!

с_СО2 = 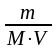= = 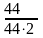0,5 моль/л; К_{с, 1000} = 0,018

Таблица материального баланса:

Компонент	С	СО2	2СО
сисх, моль/л	-	0,5	0
Δс, моль/л	-	х	2 x
сравн, моль/л	-	0,5 – x	2 x

К_с = 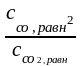= = 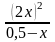0,018 Þ х = 0,0387 моль/л

с_{СО, равн} = 2^. 0,0387 = 0,0774 моль/л

с_{СО2, равн} = 0,5 - 0,0387 = 0,4613 моль/л

Р₀ = сRT = 0,5^.0,082•1000 = 41атм

Р_равн = (0,5 – х + 2х)RT = 44,173 атм Þ DР = 3,173атм

Адсорбция - поглощение одного вещества поверхностью другого вещества

Адсорбция – разновидность сорбции- поглощения одного вещества другим.

Если вещество поглощает всем объемом, то происходит

абсорбция

Адсорбция осуществляется вследствие наличия у поверхностных частиц избыточной поверхностной свободной энергии. Наличие неуравновешенной энергии у поверхностной частицы по сравнению с частицей в объеме приводит к накоплению тех или иных веществ на границе раздела фаз ( тв-г, тв-ж, ж-г) т.е. происходит повышение концентрации вещества на границе раздела фаз - адсорбция

Адсорбент - вещество, которое поглощает, адсорбирует

Адсорбат – адсорбированное вещество, которое поглощается.

Десорбция - процесс, обратный адсорбции.

Количественной характеристикой адсорбента является его удельная площадь поверхности S₀

S₀ = S/ V, м²см^-3

S₀= S/ m, м²г^-1

Чем больше S₀, тем лучше адсорбционная способность адсорбента. Большой S₀ обладают активированные угли, цеолиты, алюмосиликаты, силикагель (аморфный кремнезем) – вещества с развитой поверхностью.

S₀ активированного угля достигает величины, равной 400 – 900 м² г^-1

Количественная мера адсорбции адсорбата является величина адсорбции Г - избыток адсорбированного вещества в поверхностном слое и в объеме.

[Г]=[моль/м²]; [моль/см²адсорбента]; [моль/г адсорбента]

Физическая адсорбция

- при взаимодействии адсорбата и адсорбента возникают вандерваальсовы взаимодействия (физическая природа сил); невысокий тепловой эффект (DН₂₉₈ = –(8 – 20)кДж/моль); обратимый процесс - десорбция↑ с ростом Т.

Химическая адсорбция (хемосорбция)

- при взаимодействии адсорбата и адсорбента возникают химические связи (химическая природа сил); тепловой эффект = DН химических реакций;

необратимый процесс.

Термодинамика адсорбции

Адсорбция протекает самопроизвольно ÞDG_адс < 0.При взаимодействии адсорбата с адсорбентом теплота выделяется Þ DН_адс < 0.В процессе адсорбции происходит упорядочение адсорбированных частиц Þ DS_адс < 0.

При некоторой температуре Т_р наступает равновесие, когда скорость адсорбции равна скорости десорбции υ_ад = υ_дес

D G_адс = 0 и Т_р = DН_адс/DS_адс.

С увеличением Т адсорбция ↓, десорбция ↑.

Изотерма адсорбции - зависимость адсорбции Г от равновесной концентрации с или равновесного парциального давления р адсорбата при постоянной температуре Г = f (c), Г = f (p)

Наиболее часто используются уравнения Лэнгмюра и Фрейндлиха.

Уравнение Лэнгмюра (предполагает, что поверхность адсорбента однородна и при максимальном заполнении образуется мономолекулярный слой).

Q = Г/Г_¥(*) - степень заполнения поверхности адсорбатом.

1- Q - свободная поверхность

Г_¥ – максимальная адсорбция (при образовании монослоя);

υ_ад = k_ад(1- Q)р_А – для адсорбции газа на свободной поверхности

υ_ад = k_ад(1- Q)с_А – для адсорбции адсорбата А из раствора

υ_дес = k_десQ - пропорционально занятой поверхности

При равновесии υ_ад = υ_дес Þ k_ад(1- Q) р_А = k_десQ

К_а = k_ад/ k_дес =Q/(1- Q) р_А Þ (*)

или К_а = k_ад/ k_дес =Q/(1- Q) с_А Þ (*)

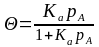или (**)

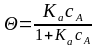Уравнение адсорбции Лэнгмюра имеет вид:

или

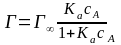
с_А – равновесная концентрация адсорбата;

р_А – равновесное давление адсорбата;

К_а – константа адсорбционного равно­весия.

При малых концентрациях и парциальных давлениях адсорбция пропорциональна концентрации или парциальному давлению.

При высоких концентрациях, когда К_ас >> 1, достигается максимальное заполнение Г = Г_¥.

Характеристики адсорбента Г_¥ и К_а находят графически по экспериментальным данным.

Уравнение Лэнгмюра (***) в координатах обратной адсорбции 1/Г и обратной концентрации 1/с

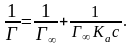
На оси ординат отсекается отрезок, равный 1/Г_¥, а tga = 1/(К_аГ_¥).

Графическое изображение изотермы адсорбции Лэнгмюра.

(Изотерма Лэнгмюра в двух формах)

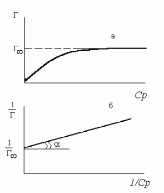
Общие закономерности адсорбции на поверхности твердых тел:

- адсорбция из растворов идет медленнее адсорбции газов,

- адсорбция зависит от природы адсорбента и адсорбата (так, актив. Уголь хорошо адсорбирует газы Cl₂, SO₂ и не адсорбирует H₂O, O₂, N₂, H₂, CO)

- сильнее из растворов адсорбируются вещества с меньшей растворимостью;

- адсорбенты, плохо смачиваемые водой (уголь, тальк)

адсорбируют органические вещества из водных растворов;

- из раствора электролита адсорбируются ионы одного вида.

Применение адсорбции

На этом явлении основаны:

- способы очистки газов и жидкостей от примесей;

- способы разделения смесей газов и жидкостей и анализ компонентов методами хроматографии;

- использование ПАВ (поверхностно активных веществ) в быту и производствах.