2. Графическое определение скоростей (построение планов скоростей).

Va = 1l1 = 0.191 = 0.19 м/с Ра = 80мм.

_v = Va / pa = 0.19 / 80 = 0.002375 (м/с)/мм V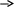 m = Va + Vm/a

Vm = Vm/о3

am = 19 мм аналог Vm/a = am_v = 190.002375 = 0.0451 м/с, и pm=64мм – аналог Vm/о3 = pm_v = 640.002375 = 0.152 м/с.

3 = Vm/о3 / l3 = 0.152 / 0,228 = 0.667 c^-1

2 = Vm/a / l22 = 0.0451 / 0.608 = 0,074 c^-1

Vd = Vb + Vd/b

AB=AM/2 следовательно ab=0,5am

Vd = Vd/о2

bd = 19 мм аналог Vd/b = db_v = 190.002375 = 0.0451 м/с, и pd=68мм – аналог Vd/о3 = pd_v = 680.005 = 0.1615 м/с.

5 = Vd/о3 / l5 = 0.1615 / 0,243 = 0.664 c^-1

4 = Vd/b / l4 = 0.0451 / 0.243 = 0,186 c^-1

О3S3 = 0.5О3M; ps3 = pm/2 О1S1 = 0.5О1A; ds5 = bd/2

ps1x = 36,5мм, s1x = _vps1x = 0,087 м/с

ps1y =-16мм, s1y = _vps1y = -0.038 м/с

ps3x = 31мм, s3x = _vps3x = 0.074 м/с

ps3y =-9мм, s3y = _vps3y = -0.021 м/с

ps4x = 61,5мм, s4x = _vps4x = 0.146 м/с

ps4y = -32мм, s4y = _vps4y = -0.076 м/с

0. Определение ускорений звеньев механизма

6. Аналитический метод

-l11sin(1) – l22f2sin(2) + l3f3sin(3) = 0

l11cos(1) + l22f2cos(2) - l3f3cos(3) = 0 получим:

-l1(1)²cos(1)–l222sin(2)–l22(2)²cos(2)+l33sin(3)+l3(3)²cos(3)=0

-l1(1)²sin(1)+l222cos(2)–l22(2)²sin(2)-l33cos(3)+l3(3)²sin(3)=0

Решая, эту систему относительно неизвестных:

3=(kctg(2)+t) / (cos(3)-sin(3)ctg(2))l3

2=(l33sin(3)+k) / (l22sin(2)), где:

k= -l1(1)²cos(1)–l22(2)²cos(2)+l3(3)²cos(3)

t= -l1(1)²sin(1)–l22(2)²sin(2)+l3(3)²sin(3)

В расчетном положении получим следующие значения:

k= -l1(1)²cos(1)–l22(2)²cos(2)+l3(3)²cos(3)=

= -0.19(-1)²cos(66)–0.608(0.074)²cos(36.9)+0.228(-0.669)²cos(74.3)=-0.052

t= -l1(1)²sin(1)–l22(2)²sin(2)+l3(3)²sin(3)=

= -0.19(-1)²sin(66,1)–0.608(0.074)²sin(36.9)+0.228(-0.669)²sin(74.3)=-0.077

3=(kctg(2)+t) / (cos(3)-sin(3)ctg(2))l3=

=(-0.052ctg(36.9)-0.077)/((cos(74.3)-sin(74.3)ctg(36.9))0.3)=0.636

2=(l33sin(3)+k) / (l22sin(2))=

=(0.2280.636sin(74.3)-0.052)/(0.608sin(36.9))=0.24

3=0,636; 2=0,24.

После дифференцирования системы (2.7):

-l1(1)²cos(1)–l22sin(2)–l2(2)²cos(2)+l55sin(5)+l5(5)²cos(5)-

–l44sin(4)–l4(4)²cos(4)=0

-l1(1)²sin(1)+l22cos(2)–l2(2)²sin(2)-l55cos(5)+l5(5)²sin(5)+

+l44cos(4)–l4(4)²sin(4)-=0

Решая, эту систему относительно неизвестных получим:

5=(kctg(4)+t)/((cos(5)-sin(5)ctg(4))l5)

4=(l55sin(5)+k) / (l4sin(4)), где:

k= -l1(1)²cos(1)–l2(2)²cos(2)+l5(5)²cos(5)–l22sin(2)–l4(4)²cos(4)

t= -l1(1)²sin(1)–l2(2)²sin(2)+l5(5)²sin(5)+l22cos(2)-l4(4)²sin(4)

В расчетном положении получим следующие значения:

k= -l1(1)²cos(1)–l2(2)²cos(2)+l5(5)²cos(5)–l22sin(2)–l4(4)²cos(4)=

= -0.19(-1)²cos(66)–0.304(0.074)²cos(36.9)+0.243(-0.662)²cos(54.7)–

-0.304(0.24)sin(36.9)–0.243(-0.183)²cos(319.6)=-0.067

t= -l1(1)²sin(1)–l2(2)²sin(2)+l5(5)²sin(5)+l22cos(2)-l4(4)²sin(4)=

=-0.19(-1)²sin(66)–0.304(0.074)²sin(36.9)+0.243(-0.662)²sin(54.7)+0.3040.24cos(36.9)-

-0.243(-0.183)²sin(319.6)=-0.024

5=(kctg(4)+t)/((cos(5)-sin(5)ctg(4))l5)=

=(-0.067ctg(319.6)-0.024)/((cos(54.7)-sin(54.7)ctg(319.6))0.243)=0.145

4=(l55sin(5)+k) / (l4sin(4))=

=(0.2430.145sin(54.7)-0.067) / (0.243sin(319.6))=0.24

5=0.145; 4=0,24.

Дифференцируем (2.8), (2.9)

S1x = -0.5l1(1)²cos(1)

S1y = -0.5l1(1)²sin(1)

S3x = -0.5l33sin(3)-0.5l3(3)²cos(3)

S3y = 0.5l33cos(3)-0.5l3(3)²sin(3)

S4x = -l55sin(5)-l5(5)²cos(5)+ls44sin(4)+ls4(4)²cos(4)

S4y = l55cos(5)-l5(5)²sin(5)-ls44cos(4)+ls4(4)²sin(4)

В расчетном положении:

S1x = -0.5l1(1)²cos(1) = -0.50.19(-1)²cos(66)=-0.038

S1y = -0.5l1(1)²sin(1) = -0.50.19(-1)²sin(66)=-0.087

S3x = -0.5l33sin(3)-0.5l3(3)²cos(3)=

= -0.50.2280.636sin(74.3)-0.50,228(-0.669)²cos(74.3)=-0.084

S3y = 0.5l33cos(3)-0.5l3(3)²sin(3)=

= 0.50.2280.636cos(74.33)-0.50.228(-0.669)²sin(74.3)=-0.03

S4x = -l55sin(5)-l5(5)²cos(5)+ls44sin(4)+ls4(4)²cos(4)=

= -0.2430.145sin(54.7)-0.243(-0.662)²cos(54.7)+0.1220.24sin(319.6)+

+0.122(-0.183)²cos(319.6)=-0,106

S4y = l55cos(5)-l5(5)²sin(5)-ls44cos(4)+ls4(4)²sin(4)=

= 0.2430.145cos(54.7)-0.243(-0.662)²sin(54.7)-0.1220.24cos(319.6)+

+0.122(-0.183)²sin(319.6)=-0,086

S1x=-0.038; S1y=-0,087 S3x=-0,084; S3y=-0.03 S4x=-0,106; S4y=-0,086

Таблица 2.6

В еличина Метод	2	3	4	5
Аналитический	0.24	0.636	0.24	0.145
Графический	0.24	0.636	0.241	0.145
отклонение	0	0	0.42	0

В еличина Метод	S1x	S1y	S3x	S3y	S4x	S4y
Аналитический	-0.038	-0.087	-0.084	-0.03	-0.106	-0.086
Графический	-0.038	-0.087	-0.084	-0.029	-0.106	-0.089
отклонение	0	0	0	0,03	0	0,03

Погрешность - в пределах допустимой.