2. Определение положений аналитическим методом.

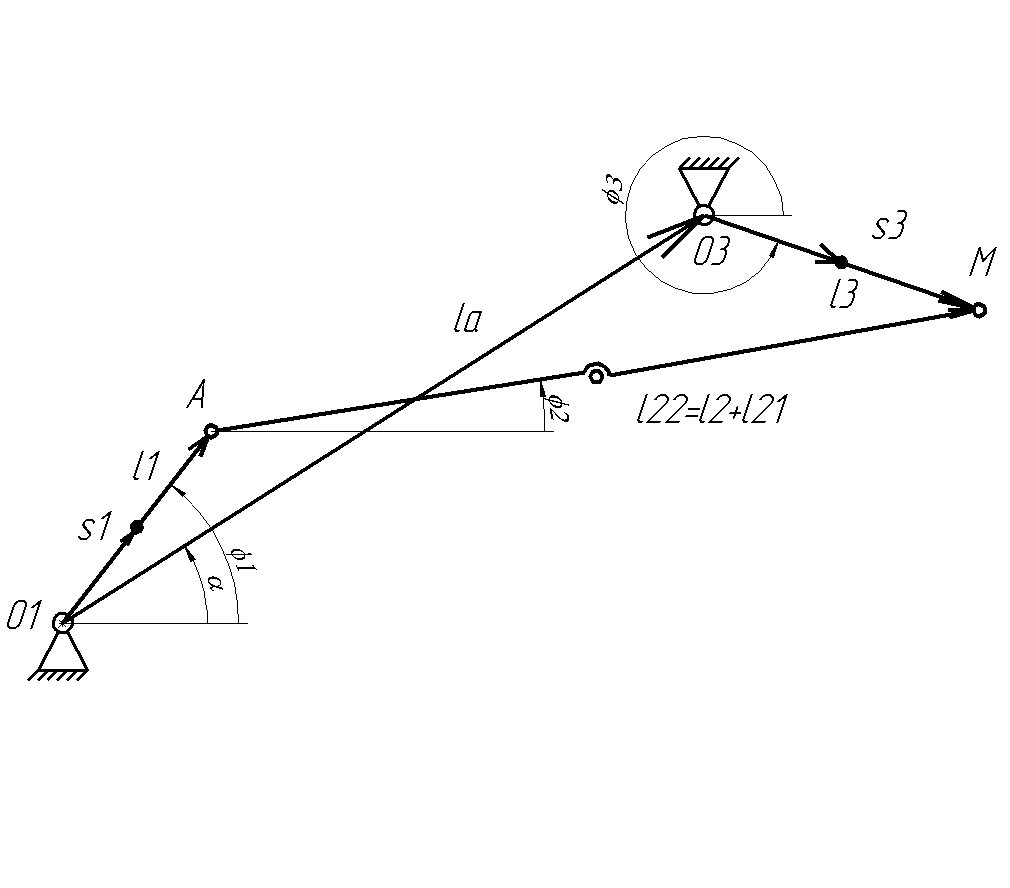
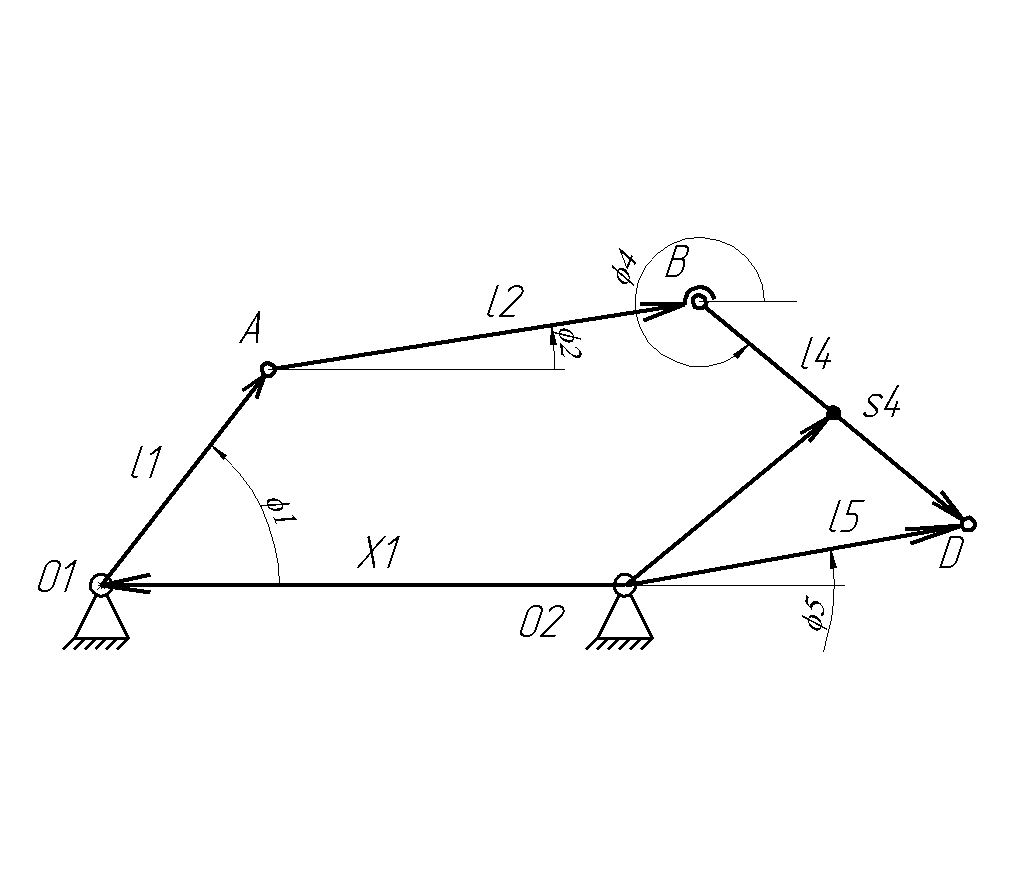
Определяем методом векторных замкнутых контуров. Рисуем схему в промежуточном положении и выявляем векторные контуры для расчета.

Первый векторный контур:

Проецируем на оси координат:

(2.1)

Проведем замену:

=arctg(y/(x1+x2))=32.47 la=((x1+x2)²+y²)^0.5=0.595м l22=0.608м

Первый векторный контур

Тогда система примет вид:

(2.2)

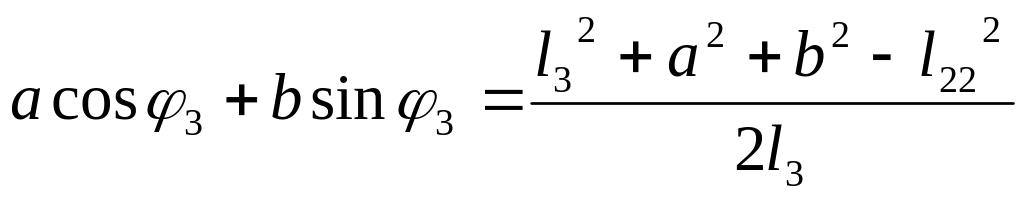
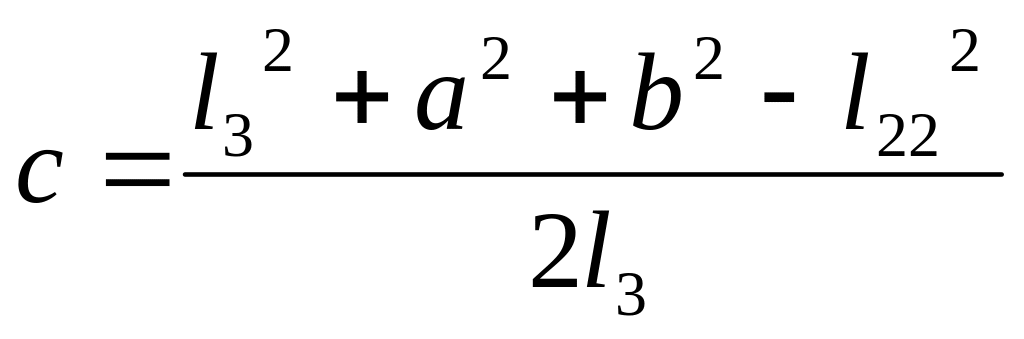
Для решения тригонометрического уравнения произведем замену:

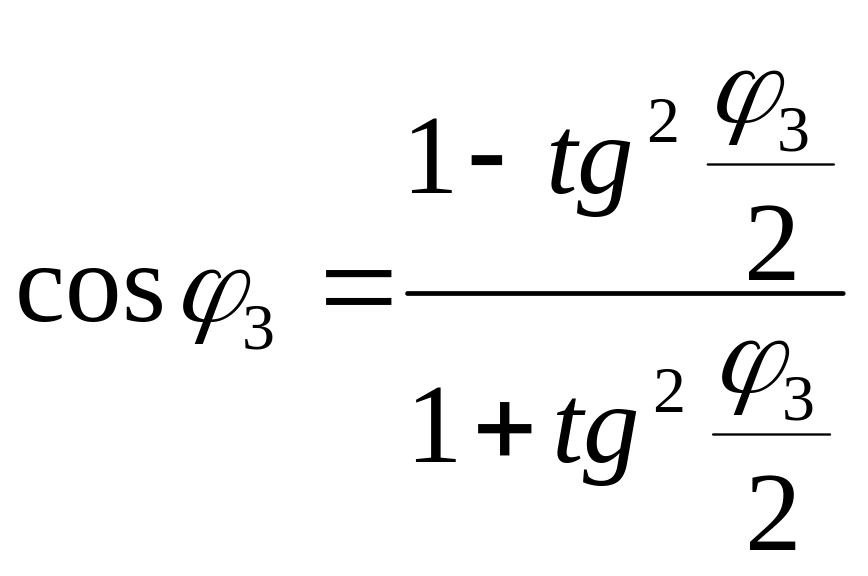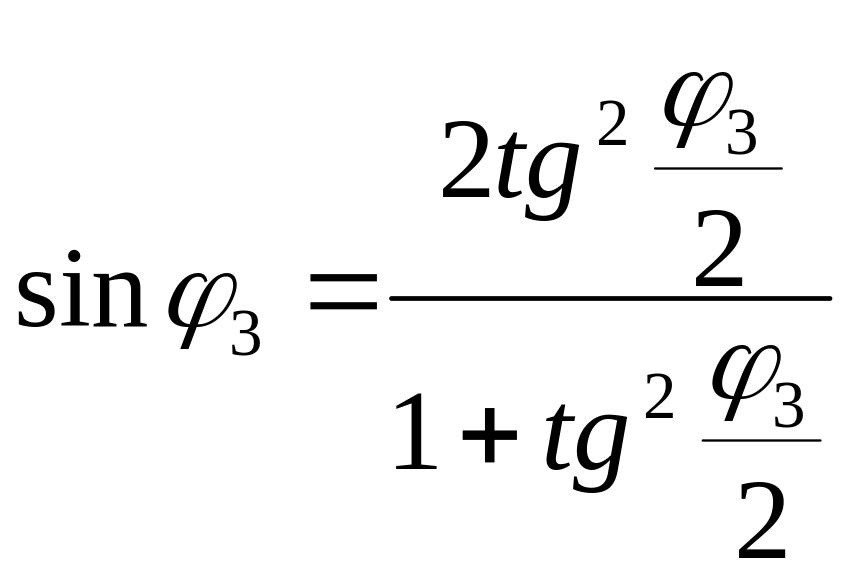и примем

тогда

или

Рассчитываем значения ₂ и ₃ в расчетном положении, решая систему при

,

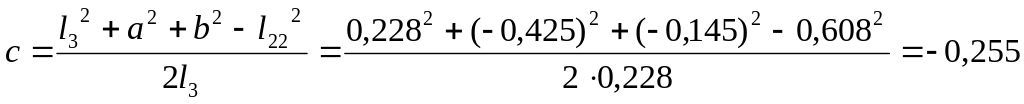
получим: ;

Значения φ₁ , φ₂ , φ₃ заносим в таблицу 2.2

Второй векторный контур

Проектируем на оси координат:

(2.2)

Проведем замену:

Тогда система примет вид:

(2.3)

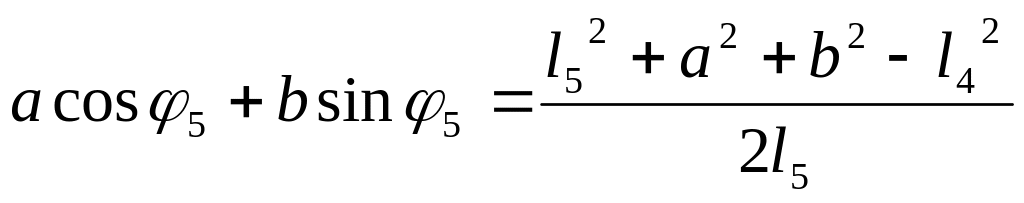
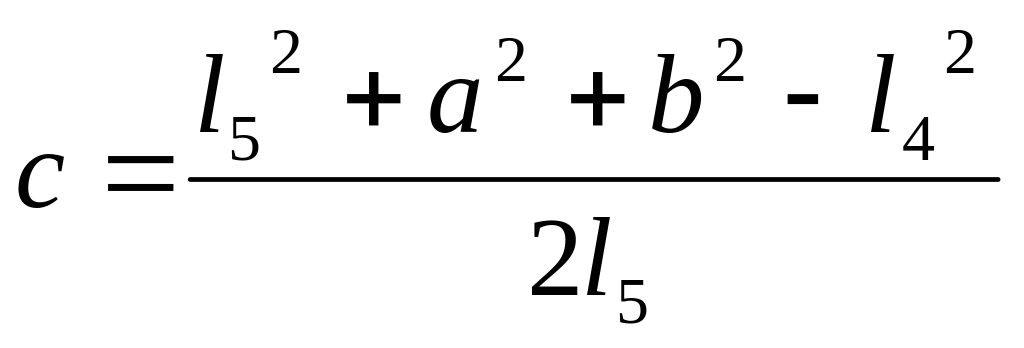
Для решения тригонометрического уравнения произведем замену:

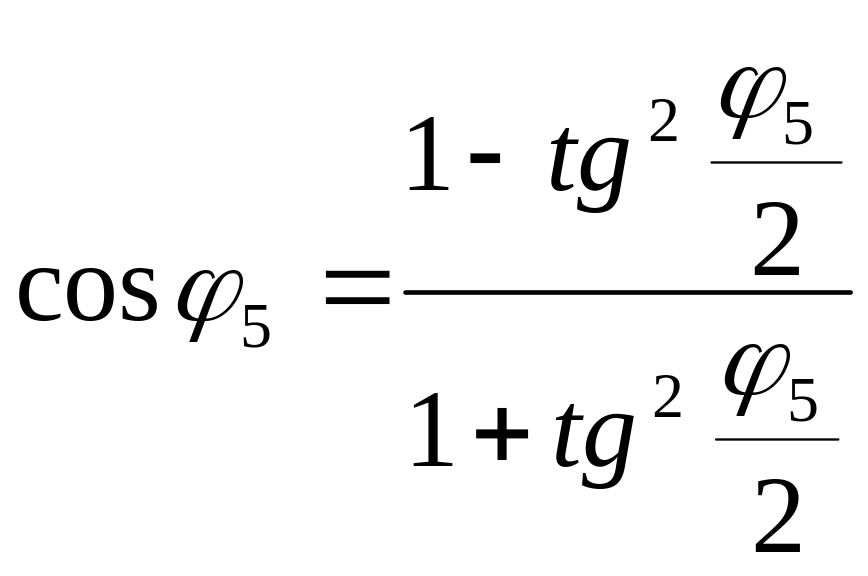и 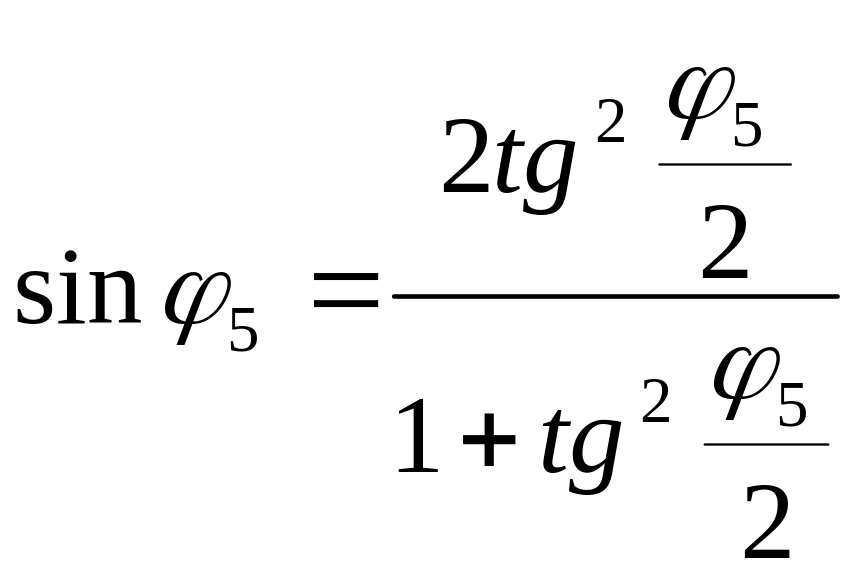примем

тогда

или

Рассчитываем значения ₄ и ₅ в расчетном положении:

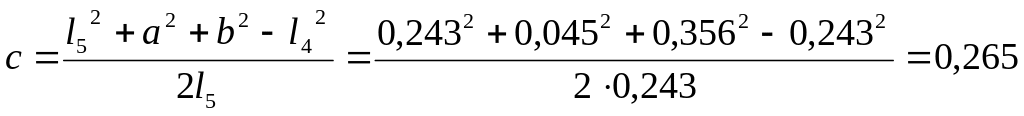
получим: ;

Значения φ₄ , φ₅ заносим в таблицу 2.2

Система уравнений для определения координат центра тяжести звеньев 1, 3, 4:

S1x = 0.5l1cos(1) S3x = 0.5l3cos(3) S4x = l5cos(5)-ls4cos(4)

S1y = 0.5l1sin(1) S3y = 0.5l3sin(3) S4y = l5sin(5)-ls4sin(4) (2.4)

S1x = 0.5l1cos(1) = 0.50,19cos(66)=0,038

S1y = 0.5l1sin(1) = 0.50,19sin(66)=0,087

S3x = 0.5l3cos(3) = 0.50,228cos(74,3)=0,031

S3y = 0.5l3sin(3) = 0.50,228sin(74,3)=0,11

S4x = l5cos(5)-ls4cos(4) = 0,243cos(54,7)-0,122cos(319,6)=0,048

S4y = l5sin(5)-ls4sin(4) = 0,243sin(54,7)-0,122sin(319,6)=0,277

В расчетном положении: S1x = 0.038м S1y = 0,087м

S3x = 0.031м S3y = 0,11м S4x = 0.048м S4y =0.277м

2.3 Определение скоростей звеньев механизма.

2. Аналитическое определение скоростей звеньев механизма.

Аналитическое определение аналдогов скоростей основано на дифференцировании по общей координате (₁) уравнений (2.1), (2.3), (2.4), (2.5).

После дифференцирования уравнений системы (2.1) получаем:

-l11sin(1) – l22f2sin(2) + l3f3sin(3) = 0

l11cos(1) + l22f2cos(2) - l3f3cos(3) = 0 (2,6)

Где 1 – аналог угловой скорости звена 1 1 = -1, т.к. ω направлена против хода часовой стрелки.

Решая систему относительно неизвестных получим:

3 = (l11(cos(1) – sin(1)ctg(2))) / (l3(cos(3) – sin(3)ctg(2)))

2 = (l33sin(3) – l11sin(1)) / (l22sin(2))

В расчетном положении

3 = (l11(cos(1) – sin(1)ctg(2))) / (l3(cos(3) – sin(3)ctg(2)))=

= (0,19(-1)(cos(66) – sin(66)ctg(36,9))) / (0,228(cos(74,3) – sin(74,3)ctg(36,92)))=-0,669

2 = (l33sin(3) – l11sin(1)) / (l22sin(2))=

= (0,228(-0,669)sin(74,3) – 0,19(-1)sin(66)) / (0,608sin(36,9))=0,074

3 =-0.669, 2 = 0.074

Дифференцируем уравнение (2.3):

-l11sin(1) – l2f2sin(2) + l5f5sin(5) – l4f4sin(4) = 0

l11cos(1) + l2f2cos(2) – l5f5cos(5) + l4f4cos(4) = 0 (2.7)

Решая систему относительно неизвестных получим:

-l11sin(1-4) – l2f2sin(2-4) + l5f5sin(5-4) – l4f4sin(4-4) = 0

l11cos(1-4) + l2f2cos(2-4) – l5f5cos(5-4) + l4f4cos(4-4) = 0

-l11sin(1-4) – l2f2sin(2-4) + l5f5sin(5-4) = 0

l11cos(1-4) + l2f2cos(2-4) – l5f5cos(5-4) + l4f4 = 0

f5=(l11sin(1-4) + l2f2sin(2-4))/ (l5sin(5-4))

f4=(-l11cos(1-4) - l2f2cos(2-4) + l5f5cos(5-4))/l4

В расчетном положении:

f5=(l11sin(1-4) + l2f2sin(2-4))/ l5sin(5-4)=

=(0,19(-1)sin(66-319,6)+0,3040,074sin(36,9-319,6))/ (0,243sin(54,7-319,6))=-0,662

f4=(-l11cos(1-4) - l2f2cos(2-4) + l5f5cos(5-4))/l4=

=(-0,19(-1)cos(66-319,6)-0,304(0,074)cos(36,9-319,6)+0,243(-0,662)cos(54,7-319,6))/0,32=-0,183

5 = -0,662, 4 = -0,183 заносим эти значения в таблицу 2.4

Дифференцируем систему (2.4):

S3x = -0.5l33sin(3) S1x = -0.5l11sin(1)

S3y = 0.5l33cos(3) S1y = 0.5l11cos(1)

S4x = -l55sin(5) + ls44sin(4)

S4y = l55cos(5) – ls44cos(4) (2.8)

В расчетном положении:

S3x = -0.5l33sin(3) = -0.50,228(-0,669)sin(74,3)=0,073

S3y = 0.5l33cos(3) = 0.50,228(-0,669)cos(74,3)=-0,021

S1x = -0.5l11sin(1) = -0.50,19(-1)sin(66)=0,087

S1y = 0.5l11cos(1) = 0.50.19(-1)cos(66)=-0.038

S4x = -l55sin(5) + ls44sin(4) =

= -0.243(-0.662)sin(54.7)+0.122(-0.183)sin(319.6)=0.146

S4y = l55cos(5) – ls44cos(4)=

= 0.243(-0.662)cos(54.7)–0.122(-0.183)cos(319.6)=-0.076

Результаты расчета скоростей в расчетном положении. Таблица 2.4

В еличина Метод	2	3	4	5
Аналитический	0.074	-0.669	-0.183	-0.662
Графический	0.074	-0.667	-0.186	0.664
отклонение	0	0.3	1.63	0.3

В еличина Метод	S1x’	S1y’	S3x’	S3y’	S4x’	S4y’
Аналитический	0,087	-0,038	0,073	-0,021	0,146	-0,076
Графический	0,087	-0,038	0,074	-0,021	0,146	-0,076
отклонение	0	0	0,01	0	0	0

Погрешность в пределах инженерной. Расчеты считаем верными.