1.Структурный анализ механизма.

1.1. Рисуем структурную схему машины (рис.1.2).

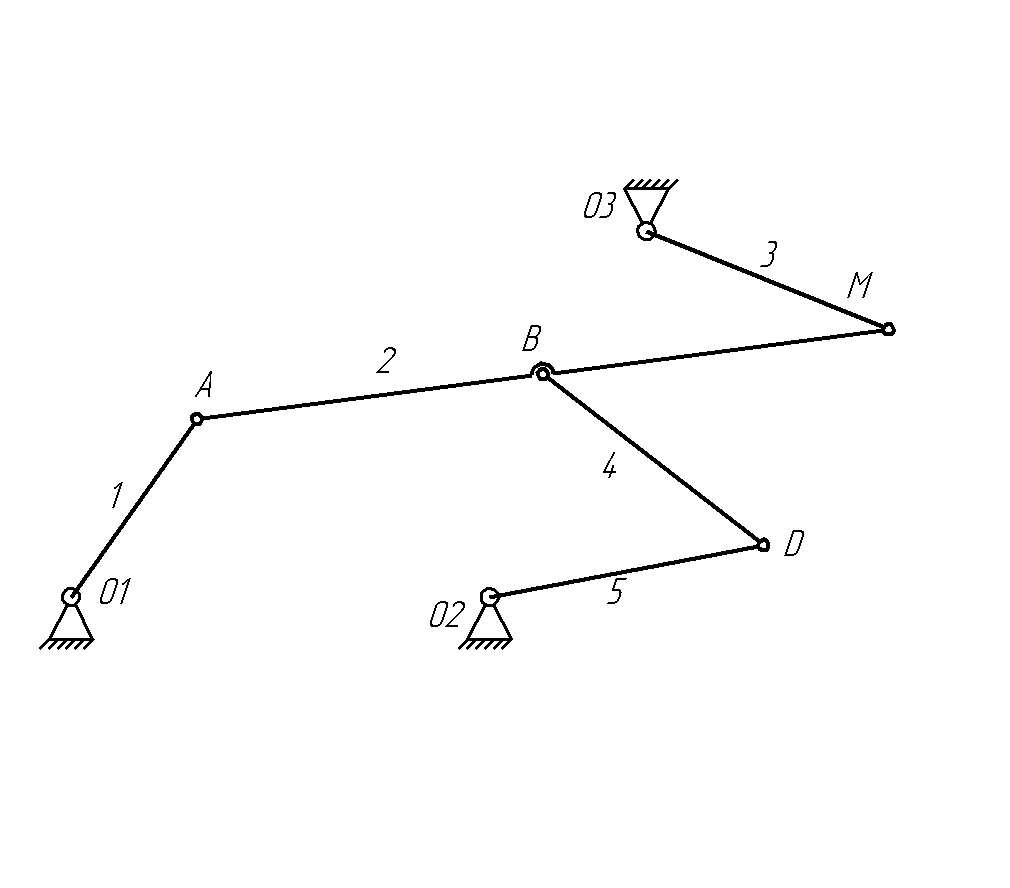
Рис.1.2. Структурная схема машины

1.2. Выявляем сложные и разнесённые кинематические пары.

Данный механизм не содержит разнесенных и сложных кинематических пар.

1.3. Класифицируем кинематические пары: определяем их название; подвижность; количество пар одной подвижности; общее количество пар одной подвижности ; общее количество кинематических пар в механизме; вид реализуемого в паре замыкания; вид контакта элементов кинематических пар ( высшие – низшие) Таблица 1.2.

Классификация кинематических пар

Таблица 1.2

№ п/п	Номер звеньев, образующих пару	Условное обозначение	Название	Подвижность	Высшая /низшая	Замыкание	Открытая /закрытая
1	0-1	О1	Вращательная	1	Н	Г	З
2	1-2	А	Вращательная	1	Н	Г	З
3	2-3	M	Вращательная	1	Н	Г	З
4	2-4	B	Вращательная	1	Н	Г	З
5	0-3	О3	Вращательная	1	Н	Г	З
6	4-5	D	Вращательная	1	Н	Г	З
7	5-0	О2	Вращательная	1	Н	Г	З

Исследуемый механизм состоит только из одноподвижных кинематических пар ,где число одноподвижных кинематических пар в механизме, - общее число кинематических пар в механизме.

1.4. Подсчитываем и классифицируем подвижные звенья механизма.

Классификация звеньев

Таблица 1.3

№ п/п	Номер звена	Условное обозначение	Название	Движение	Число вершин (t)
1	0	О1, О2, O3	Стойка (0)	Отсутствует	-
2	1	О1 А 1	Кривошип (1)	Вращательное	2
3	2	M A В	Шатун (2)	Сложное	3
4	3	M О3	Кулиса (3)	Вращательное	2
5	4	B D	Шатун (4)	Сложное	2
6	5	D О2	Кривошип (5)	Вращательное	2

Механизм имеет четыре двухвершинных (t=2) линейных звена; одно трехвершинное (t=3) звено 2, которое является базовым; пять (n=5) подвижных звеньев.

1.5. Определяем число присоединений подвижных звеньев к стойке.

Механизм имеет три (S=3) присоединений к стойке.

1.6 Выделяем в исследуемом механизме самостоятельные структурные группы, элементарные и простые механизмы , а также механизмы с разомкнутыми кинематическими цепями .

В данном механизме можно выделить один элементарный механизм. (рис.1.3)

O1

1

Рис 1.3. Элементарный механизм

И два простых, шарнирный четырехзвенник и двухподвижный пятизвенник

(рис 1,4),

C

О1

А

M

О3

О2

D

О3

B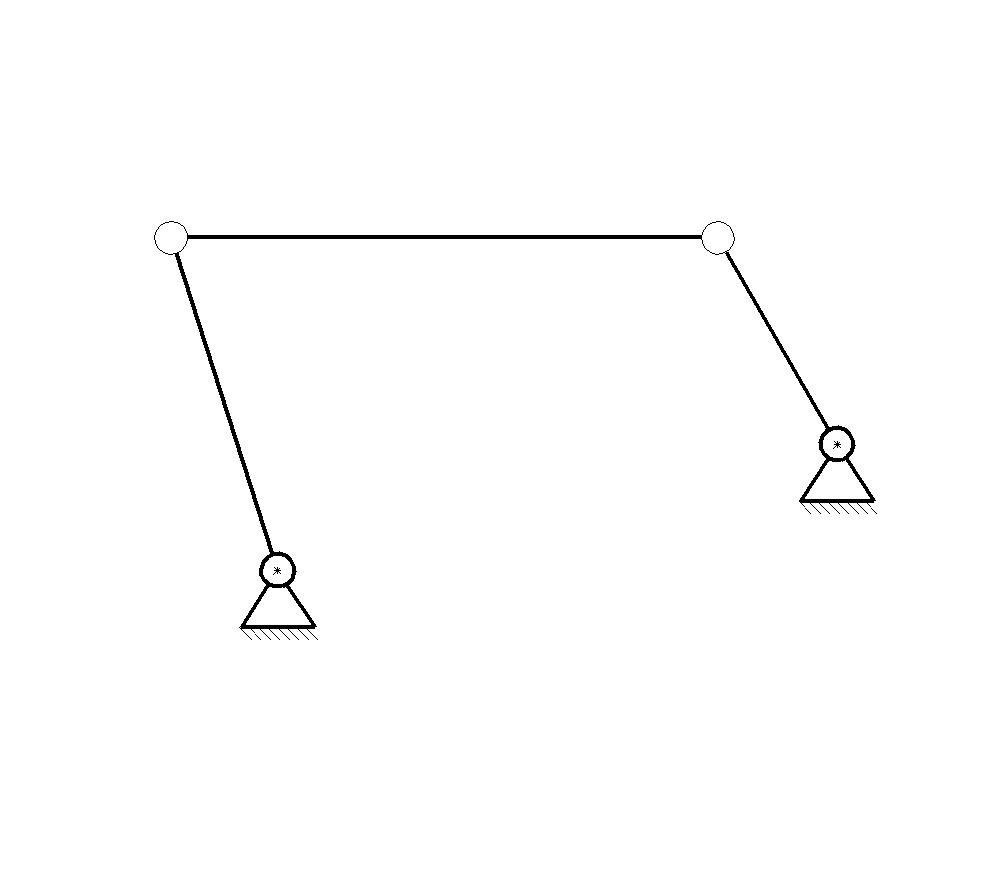

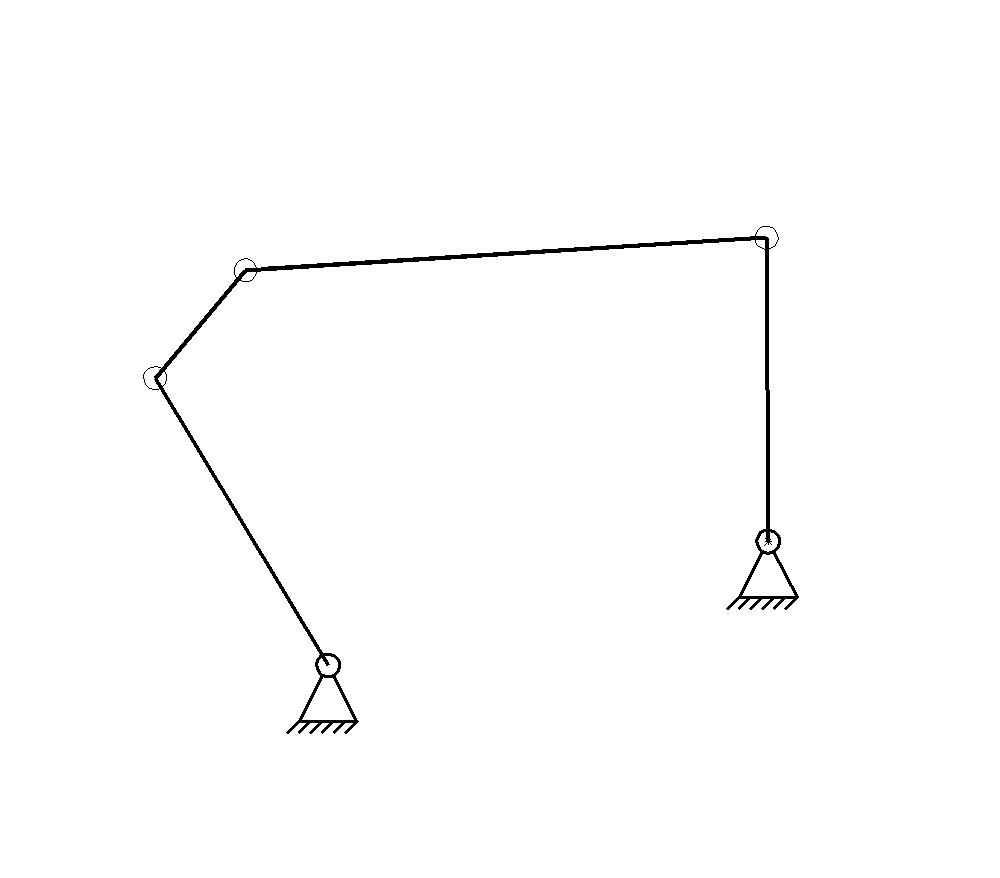
Рис. 1.4.

Механизмов с разомкнутыми кинематическими цепями нет

1.7. Выявляем простые стационарные и подвижные механизмы. Сложный механизм имеет в своем составе только простые стационарные механизмы.

1.8. Находим звенья закрепления и присоединения. В исследуемом сложном механизме звеньев закрепления нет. У него одно звено присоединения - звено 2 (шатун). Звено 2 одновременно входит в два простых механизма –шарнирный черырехзвенник и двухподвижный пятизвенник. Значит для этого звена .

1.9. Классифицируем механизм. Исследуемый механизм имеет постоянную структуру, является сложным.

1.10. Определяем подвижность простых механизмов.

Анализ движений звеньев механизма и элементов кинематических пар показывает, что и исследуемые простые механизмы, и сам сложный механизм существуют в трехподвижном пространстве, в котором разрешены следующие простейшие независимые движения:

• два поступательных x и y вдоль соответствующих осей

• одно вращательное 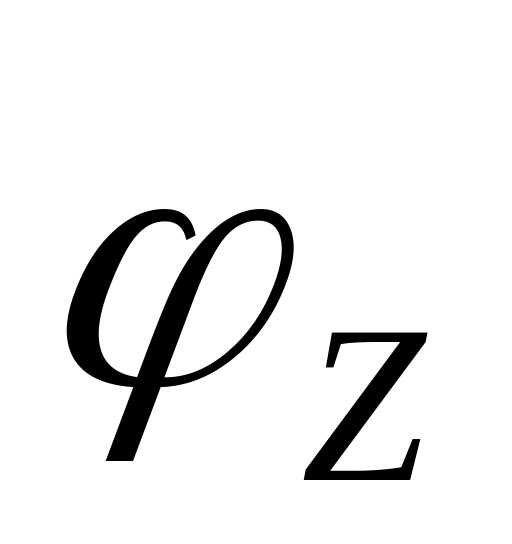вокруг оси Z.

Подвижность механизмов находиться по формуле:

(1.1)

где W – подвижность механизма;

n – число подвижных звеньев механизма;

– число кинематических пар i-той подвижности;

Определим подвижность шарнирного четырехзвенника. Mеханизм имеет: три подвижных звена; четыре одноподвижные кинематические пары. Тогда его подвижность определиться:

1.11. Определяем подвижность сложного механизма.

Подвижность сложного механизма определяется по формуле:

(1.2)

1.12. Выделяем в исследуемом устройстве механизм I класса. В соответствии с классификацией И.И. Артоболевского механизм I класса для исследуемого механизма совпадает с элементарным механизмом.

1.13. В

В

ыделяем структурные группы Ассура. В механизме можно выделить следующие структурные группы (рис.1.5):

D

А

M

О3

B

O2

Рис.1.5. Структурные группы Ассура

1.14. Проверяем, распадаются ли выделенные структурные группы на более простые. Видно, что выделенные структурные группы являются самыми простыми для трехподвижного пространства, в котором существует исследуемый механизм, и, значит, они не могут иметь в своем составе другие более простые группы Ассура.

1.15. Проводим классификацию структурных групп по И.И. Артоболевскому

Классификация структурных групп

Таблица 1.4

№ п/п	Структурная схема	Номер звеньев, образующих группу	Класс, порядок, вид
1	O1 1	0-1	Механизм I класса
2	O3 M 3 A 2	2-3	II класс 2 порядок 1-вид
3	O2 D B 4 5	4-5	II класс 2-порядок 1-вид

1.16. Определяем класс сложного механизма.

Механизм относится ко II классу.

2. Кинематический анализ механизма

2. Определение крайних положений механизма аналитическим методом

Начальное положение.

Это положение должно реализовываться, когда звенья О1А и АM выстраиваются в одну линию, причем О1M = АM - О1А.

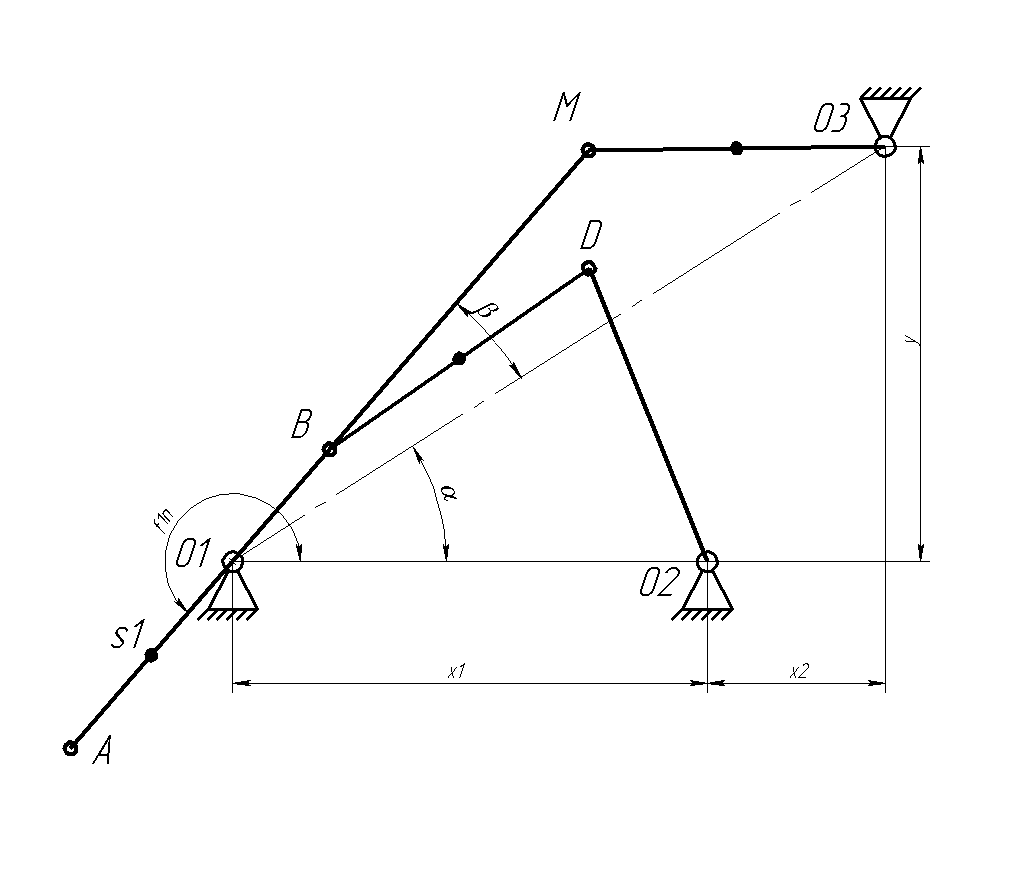
_н=f1n=180++

где

O1O3=la=((x1+x2)²+y²)^0.5=((0.365+0.137)²+0.319²)^0.5=0.595

AM=l22=AB+BM=0.304+0.304=0.608м

 β определим из треугольника О1О3М по теореме косинусов:

=arccos((O1M²+O1O3²-O3M²)/(2O1MO1O3)=

arccos(((0.608-0.19)²+0,595²-0.228²)/(2(0.608-0.19)0.608) =16.6

_н =180+16,6+32,47=229.111

_к=f1k= +

 β определим из треугольника О1О3М по теореме косинусов:

=arccos((O1M²+O1O3²-O3M²)/2O1MO1O3)=

arccos(((0,608+0,19)²+0,595²-0,228²)/(2(0,608+0,19)0,608) =8.57

_к =32,47+8,57= 41.04

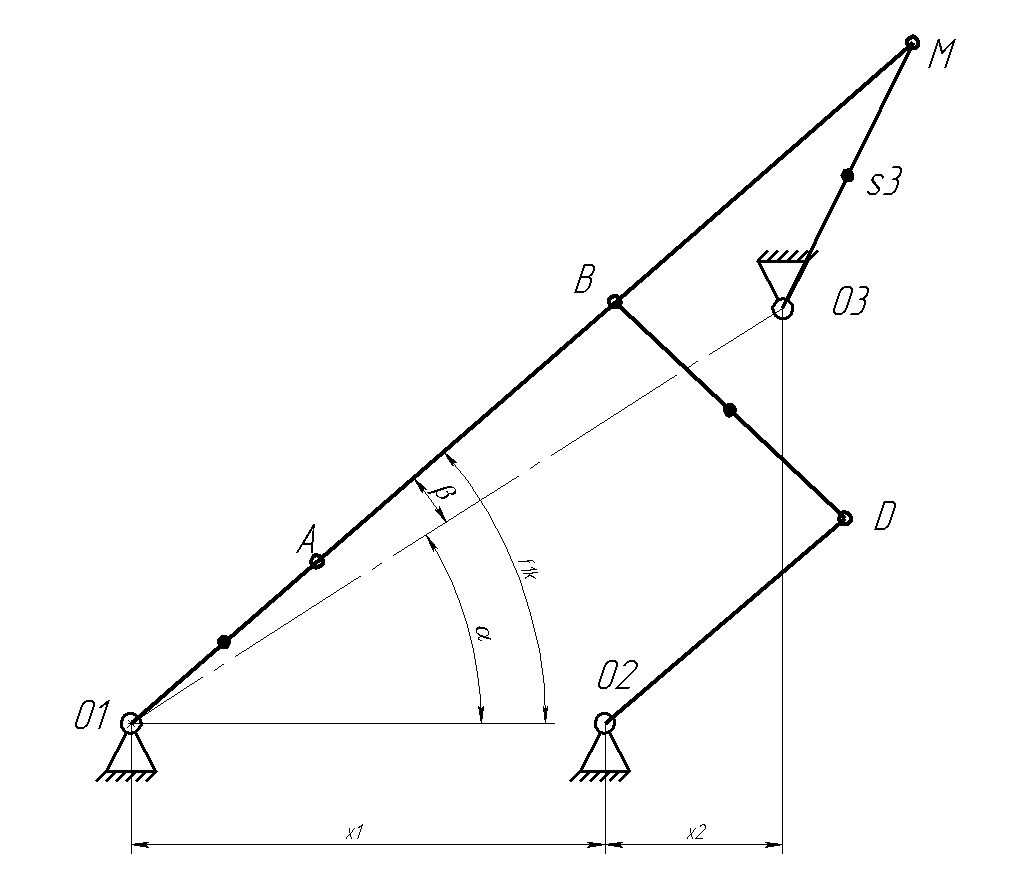
2. Графическое построение планов положения исследуемого механизма.

Выбираем масштабный коэффициент длин _l = 0.19/80=0,002375 м/мм и рассчитываем чертежные размеры звеньев (табл. 2.1).

Таблица 2.1

	О1А	АВ	ВM	MО3	BD	DО2	Х1	Х2	Y1
	l1	l2	l21	l3	l4	l5	X1	X2	Y1
м	0,19	0,304	0.304	0.228	0.243	0.243	0.365	0.137	0.319
мм	80	128	128	96	102.4	102.4	153.6	57.6	134.4

Планы механизма на чертеже строим следующим образом:

• Отмечаем на чертеже неподвижные точки О1, О2, О3, рисуем в них вращательные кинематические пары.

• Проводим траектории движения: точки А – окружность радиусом О1А из т. О1; точки D – дугу радиусом О2D из т. О2; точки M – дугу радиусом О3M из т. О3;.

• Начиная от точки А₀ окружность радиуса О1А делим на 12 частей.

- Точки деления обозначаем А₁ А₂ А₃ ….в направлении вращения звена О1А.

- Строим положения кривошипа, соединяя точки Вi с Аi

- Методом засечек строим план положений механизма для каждого положения кривошипа

- C помощью обратного построения определяем положения начала действия момента Mc. Рабочий ход звена 5 составляет 5_max=75,1, момент дначала действия Мc при 5=0,45_max =30,04, отсчитывая от положения 0 в сторону вращения звена 5. Этому положению соответствует 1=109,56.

- При построении планов механизма отмечаем положения центров масс звеньев 1, 3, 5 и строим их траектории.

- Проверяем с помощью линейки и транспортира углы наклона (в положении 6), результаты измерения заносим в таблицу 2.2.

Результаты расчета в расчетном положении.

Т аблица 2.2

Величина Метод	10	20	30	40	50
Аналитический	66	36,9	74,3	319,6	54,7
Графический	66	37	74	320	55
Отклонение	0	0,27	0,41	0,13	0,55

Величина Метод	S1x.M	S1y.M	S3x.M	S3y.M	S4x.M	S4y.M
Аналитический	0.038	0.087	0.031	0.11	0.048	0.277
Графический	0.038	0.087	0.031	0.109	0.047	0.278
Отклонение	-	-	-	-	-	-

Погрешность не превышает инженерной (5 %), следовательно, расчеты можно считать верными.