
- •Қазақстан республикасының ғылым және білім министрлігі қ.И. Сәтбаев атындағы қазақ ұлттық техникалық университеті
- •Студенттің пәндік
- •Алматы 2007
- •1 Пәннің оқу бағдарламасы – syllabus
- •1.1 Оқытушы туралы мәліметтер:
- •1.2 Пән туралы мәліметтер:
- •Оқу жоспарының көшірмесі
- •1.6 Тапсырманың түрі және мазмұны, олардың орындалу графигі
- •1.7 Әдебиеттер тізімі
- •1.8 Білімді бағалау және бақылау
- •Модульдер мен аралық аттестация бойынша бақылау жүргізуге арналған сұрақтар тізімі
- •1 Модуль бойынша бақылауға арналған сұрақтар
- •2 Модуль бойынша бақылауға арналған сұрақтар
- •Аралық бақылауға арналған сұрақтар.
- •1.9 Пәннің саясаты мен процедурасы
- •2 Негізгі таратылатын материалдар тізімі
- •2.1 Курстың тақырыптық жоспары
- •2.2 Дәріс сабақтарының мазмұны Дәріс 1. Ғылыми зерттеулердің жалпы әдістемесі
- •Дәріс 3. Бұрғылаудағы эксперименттік мәліметтерді статистикалық бөлшектеу
- •Дәріс 4. Таңдау мәліметтері бойынша генеральді жиынтықтың бағасы
- •Дәріс 5. Тәжірибелік деректерді үлестіру түрлері
- •Дәріс 6. Таңдама сипаттамасының дәлдігі
- •Дәріс 7. Бұрғылаудағы тәжірибелік тәуелділіктер
- •Дәріс 8. Экспериментке дайындық және оның нәтижелерінің алдын ала сараптамасы
- •Дәріс 9. Тік сызықты тәуелділік моделінің математикалық құрылымы
- •Дәріс 10. Параболалық тәуелділік моделінің математикалық құрылымы
- •Дәріс 11. Көп факторлы тәжірибелі тәуелділіктер
- •Дәріс 12. Тәжірибелерді оңтайландырудың негіздері
- •5 Сурет. Түзетумен оптимумға қозғалыс және нөлдік нүктенің аймағындағы тәжірибе жоспары.
- •Дәріс 13. Градиент әдісімен оптимумды іздеу
- •Дәріс 14. Оптимальді аумақ төңірегіндегі зерттеу
- •Дәріс 15. Бұрғылау үрдісін модельдеу
- •2.3 Зертханалық жұмыстардың мазмұны
- •2.4 Студенттің оқытушымен өзіндік жұмыстар сабақтарының мазмұны (соөж)
- •2.5 Студенттердің өздік жұмысы бойынша сабақ жоспары (сөж)
- •2.6 Өзін бақылау үшін тестік тапсырмалар
- •2.7 Курстық жұмысты орындау қойылатын талаптар
- •Өтетін курс бойынша сұрақтар тізімі
- •2.9 Глоссарий
- •Мазмұны
- •050706 «Геология және пайдалы қазбалар кен орындарын барлау» мамандығына арналған
- •Студенттің пәндік
- •Федоров Борис Владимирович Айтугулова Баян Андреевна
Дәріс 5. Тәжірибелік деректерді үлестіру түрлері
Тәжірибеден алынған деректерді сараптау кезінде сәйкес келетін басты жиынтықтар нормальды заңға (Гаусс заңы) сәйкес үлестіру деп ұйғаруға негіз бар.
Кездейсоқ шама нормалды заңға сәйкес үлестіргені дәлелденді. Көптеген тәуелсіз факторлардың әсерінің нәтижесі болған жағдайдағы оның үстіне әрбір нұсқа осы факторлардың жиынтық әсерінен құрылады.
Нормалды үлестірім тығыздығы нормалды заңға сәйкес мына формуламен өрнектеледі.
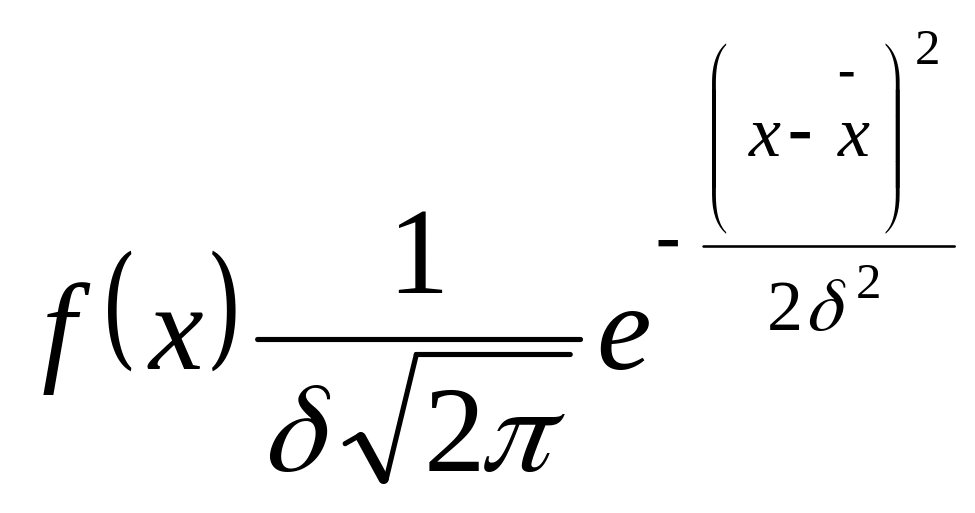 (48);
(48);
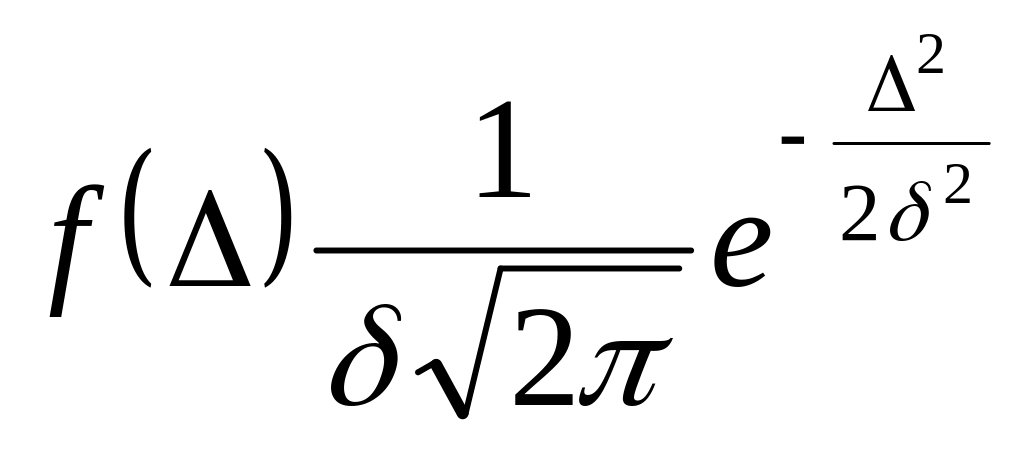 (49);
(49);
![]() (50)
(50)
Нормальды заңға бұрғылауға тән бұрғылаудың берілген жыныс күйіне қарай механикалық жылдамдығы, кашауға берілген номинальды диаметрі бар коронкалардың нақты диаметрі сияқты шамалардың үлестірімі жауап береді.
Вариациялық қатардың барынша мүмкін мәндерінің интервалы
![]() (51)
(51)
Х кездейсоқ шама осы интервалда
![]() сенімділігімен бекітілген.
сенімділігімен бекітілген.
«Үш сигма» критерийі жалпыға бірдей критерий болып табылады.
Шағын ассиметриялық үлестірім логарифмдік нормальды заңмен сипатталады. Бұл үлестірім заңының ерекшелігі сол, оған бағынатын кездейсоқ шама (нормальды заңдағы сияқты) көп мөлшердегі тәуелсіз факторлар әсерінің нәтижесі болып табылады. Әрбір жеке нұсқа осы факторлардың қосындысын емес көбейтіндісінің әсерінен құрылады.
Егер х кездейсоқ
шама логнормальды заңға бағындырылған
болса, онда одан шығатын,
![]() шамасы нормалды үлестірім
болып табылады.
Көптеген теориялық үлестірім
заңдарын басты жиынтық көлемі 20-30 асатын
таңдама мәліметтері бойынша сипаттауға
қолданады. Алайда, тәжірибе жүзінде
мұндай көлемде мәндер алу мүмкіндігі
көп жағдайда болмайды.
шамасы нормалды үлестірім
болып табылады.
Көптеген теориялық үлестірім
заңдарын басты жиынтық көлемі 20-30 асатын
таңдама мәліметтері бойынша сипаттауға
қолданады. Алайда, тәжірибе жүзінде
мұндай көлемде мәндер алу мүмкіндігі
көп жағдайда болмайды.
Сенімділік интервалдар мен сенімділік ықтималдылығын жалпылама бағалау үшін кіші таңдама нәтижесі бойынша тығыздығы мына түрде берілетін Стьюдент үлестірімі қолданылады:
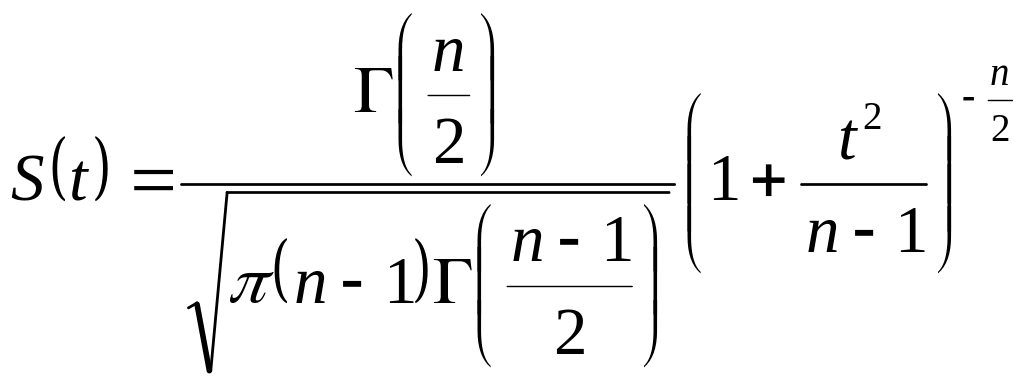 (52)
(52)
Мұнда, п
– берілген таңдамағы сан,
![]() ;
;
![]() –
–
![]() аргументтен гамма-функция.
аргументтен гамма-функция.
![]() функциясы
функциясы
![]() -ның
бірдей оң және теріс абсолютті мәні
бойынша бірдей, яғни симметриялы ж/е
-ның
бірдей оң және теріс абсолютті мәні
бойынша бірдей, яғни симметриялы ж/е
![]() болғанда максимум болады,
-ның
абсолютті мәнінің өсуі кезінде функция
асимптотиялық нольге жақындайды.
болғанда максимум болады,
-ның
абсолютті мәнінің өсуі кезінде функция
асимптотиялық нольге жақындайды.![]() (>
20
(>
20![]() 30)
болғанда Стьюдент үлестірімі
нормальды үлестірімге
өтеді, керісінше п азайғанда айырмашылық
өседі. Көрсеткішті үлестірім
шұғыл ассиметриялы болып табылады және
мына дифференциалды функциямен
өрнектеледі:
30)
болғанда Стьюдент үлестірімі
нормальды үлестірімге
өтеді, керісінше п азайғанда айырмашылық
өседі. Көрсеткішті үлестірім
шұғыл ассиметриялы болып табылады және
мына дифференциалды функциямен
өрнектеледі:
![]() (53)
(53)
Х-тек оң шама ғана бола алады. (X>0). Бұл үлестірімнің ерекшелігін мына қатынаспен көрсетеді:
![]() (54)
(54)
Көрсеткішті үлестірімнің интегралды функциясы:
![]() (55)
(55)
Көрсеткішті заң деп, әдетте көптеген детальдардан құрылған әртүрлі күрделі құрылғылардың (механизм, аспаптар, станоктар) істен шығуына жасалған үлестірілімді сипаттау қабылданады.
"хи-квадрат" үлестірімі дифференциалдық функциямен сипатталады.
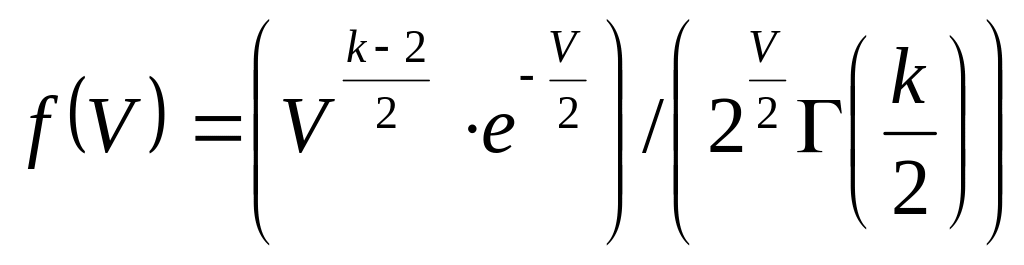 (56)
(56)
Здесь
-величина,
распределенная по закону "хи-квадрат",
причем
![]() ,
,
![]() -
основание натуральных логарифмов
-гамма-функция, К-число
степеней свободы:
-
основание натуральных логарифмов
-гамма-функция, К-число
степеней свободы:
мұнда: V – кезінде хи-квадрат заңы бойынша үлестірілген шама;
е – гамма функциясы натуралды логарифмнің негізі;
К – еркіндік дәрежесінің саны:
![]() (57)
(57)
хи-квадрат үлестірімі таңдамадағы мүшелер санына тәуелді. Оған мына қатынас лайық:
![]() (58)
(58)
мұнда: k – орташа мән;
D – дисперсия.
Кіші К үшін
үлестірім өткір ассиметрияны, мүшелер
санының өсуіне қарай ассиметриялық
қасиет азаяды.
![]() кезінде хи-квадрат үлестірімі нормальды
үлестірімге өтеді.
кезінде хи-квадрат үлестірімі нормальды
үлестірімге өтеді.
Үлестірімнің интегралды функциясының түрі мынадай:
![]() (59)
(59)
НЕГ 1 [97-112 бет], ҚОС 5 [26-36 бет]
Бақылау сұрақтары:
Кәдімгі орналастыру заңының қасиеттері?
Кәдімгі логарифмдік орналасу заңы қашан қолданылады?
Қандай үрдістер Стьюдентті орналастырумен сипатталады?
Қандай үрдістер орналасу көрсеткіштерімен сипатталады?
Қандай жағдайларда «хи-квадрат» орналасуы нақты орналасуға ауысады?
