Дәріс 3. Бұрғылаудағы эксперименттік мәліметтерді статистикалық бөлшектеу

Эксперименттік тексеру әдісінде нақты қабілеттілікті тексеру нәтижесінде анализ жасалады. Барлық нақты көріністер (статистикалық бірліктер) тексеру объектісіндегі анықтамамен сәйкестенсе – басты жиынтықты құрайды.

Әрбір берілген бірліктердің басты жиынтығы (рейстер, станоктар және т.б.) белгілеріне қарай табиғаты ортақ болып саналады. Егер басты жиынтықтың барлық мүшесінің ортақ мәні негізгі әсер етуші факторға шартталған болса онда бір мүшенің екіншісінен айырмашылығы екінші сатылы факторларға байланысты.

Кездейсоқ басты жиынтықты таңдау вариациялық қатар деп аталады, тексеру белгісінің мәніне қарай таңдауға тексерілудегі басты жиынтық берілген мәндерін қосуға болады. Осыған орай бір бірліктерді басқалардың алдында беруге болмайды. Таңдау кезінде мүшелер саны көп болуы керек. Вариациялық қатардағы бөлек мүшелер вариант деп аталады. Варианттар арасындағы айырмашылық вариациялық жиынтық ішінде өзгеру белгісімен мінезделеді. Егер варианттар тәжірибе жүргізілген ретпен жазылса, онда вариациялық қатар реттелмеген деп аталады.

Реттелген қатарда варианттар өсу немесе төмендеу ретімен орналасады. Берілген таңдамадан мінездеме алу мақсатында вариациялық қатар математикалық статистика әдісімен өңделеді. Егер варианттар саны тең болса, онда бұл таңдау кіші деп аталады. Тәжірибе бағасы жоғары болған сайын, таңдау көлемі аз болады. Түгелдей алғанда вариациялық қатар ара-қашықтық (топталған) түрде болады. Осы мақсатта реттелген варияциялық қатар түрі: ( – вариант нөмірі) ара-қашықтықтарға бөледі, әрқайсындағы мәндер шамалы өзгереді. Бұл өзгеру белгісі - қадамы деп аталады. Әрбір ара-қашықтықтың ішіндегі белгілер мәні олардың орта мәні ( – арақашықтық нөмері) алмастырылады.

(16)

мұнда: және – сәйкесінше ара-қашықтықтың төменгі және жоғарғы шекарасының

белгі мәні.

Берілген вариант ара-қашықтығына түскен сан – жиілік деп аталады. Осыған байланысты әрбір – ара-қашықтықта мүшесі бар. Әрбір ара – қашықтық мәні - . Онда

(17)

мұнда: – қатардағы варианттардың ортақ саны.

Арақашықтық қатарды құрастыру үшін, алдымен оның құрамын табу керек:

(18)

Арақашықтықтың рационал сан мәні Стерджес формуласын береді:

(19)

Бұл қатарды төмен және жоғары сан мәнімен оңай өңдеуге мүмкіндік береді. Анықталған және бойынша қадамды анықтаймыз:

(20)

Әры қарай топтама жасалады. Арақашықтық шекарасын тапқан соң мәнінің орташа ара-қашықтығын анықтаймыз және әрбір арақашықтықтағы варианттар санын есептейміз. Жиіліктің белгі пайда болуының оның мәніне қатынасы – бөлшектеу деп аталады.

Жекелік таңдау көлеміне қатысты жиілік – жекелік деп аталады.

(21)

(17) формуладан, қосынды

(22)

нөмірі арақашықтыққа жиналған жекелік

(23)

Бөлшектеу тығыздығының формуласы:

(24)

Графика – эмпирикалық бөлшектеу бәрінен бұрын гистограмма және кумулят деп аталады (1 – сурет а, б). Абсцисса бойынша екі графиктеде тексерудегі белгі арақашықтық мәні жатқызылған. Ордината бойынша гистограмманың бөлшектеу тығыздығын немесе оның пропорционал мәні немесе қалдырылады. Гистограмма вертикаль және горизонталь бөлімдерде сынық сызықпен көрсетілген және соңғы шекара ара-қашықтық шекарасына сәйкес келеді.

Гистограммадан модальды аралықты оңай табуға болады, яғни көп вариант саны түскені (максимал және жекелік). Жоғарғы бөлшектеу тығыздығына сәйкес келетін вариант мәнін – мода деп атайды. Куммулятта ординат бойынша жиналған жекелікті қалдырады.

а – гистограмма б – кумулята

1 – сурет. Гистограмма мен кумулятты тұрғызу мысалдары

Кумулятта варияциялық қатардың жекелігін кез-келген таңдалған аралық мәнді ( х=А х=В дейін) орнатуға мүмкіндік береді. Бұл жиілік

(25)

мұнда: және – А және В нүктесі үшін жиналған жекелік.

Бұдан жақша ішіндегі айырмашылық берілген аралықтағы варияциялық қатар екендігі көрсетілген.

(26)

онда

(27)

Кумулята кері есепті шығаруға мүмкіндік береді, яғни берілген жекелікке сәйкес келетін вариант мәнін табады. Бұндай мән – квантиль деп аталады.

Вариациялық қатардың дисперсия және моменттің орташа мәні.

Варияциялық қатардың дисперсия және моменттің орташа мәні. Варияциялық қатардың керекті мағынасы -тің орташа мәні болып табалады. Топталмаған қатардың орташа мәні

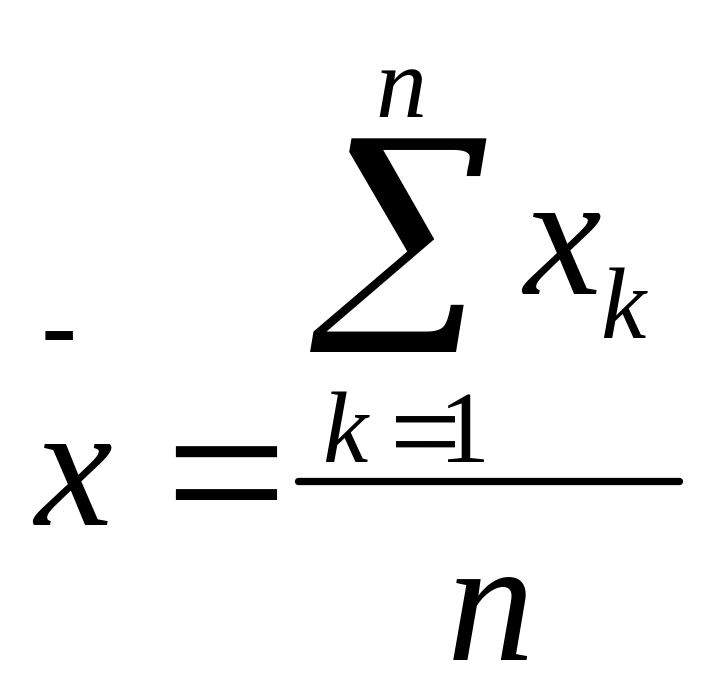, (28)

мұнда: к – вариант нөмірі. Аралық қатар үшін

немесе 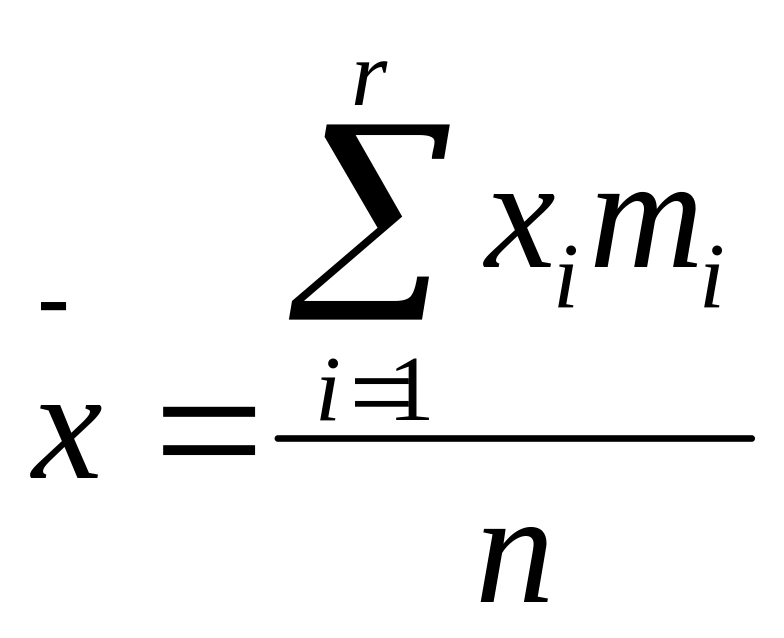(29)

(28) және (29) формула бойынша орташа мән – орташа арифметикалық деп аталады.

Симметриялы варияциялық қатарда гистограмма симметриялық фигура шамасында болады, орташа мәні модаға тән. Симметриялық емес сатысын ассиметрия коэффициенті айқындайды.

(30)

мұнда: – орташа квадратты ауытқу.

Егер мода орташа мәннің сол жағында ( ) болса, онда – плюс белгісінде болады, және асимметрия оң жақты деп аталады, қарсы жағдайда сол жақты деп аталады. Информацияда таңдаманың орташа мәнін есептеуде қосымша оның мүшелерінің өзгергіштігі (варияциясы) жайында анықтама болуы қажет. Барлық таңдаманы түгелдей алғандағы өзгергіштік көрсеткіші дисперсия деп аталады. Қатарларды топтастыру үшін:

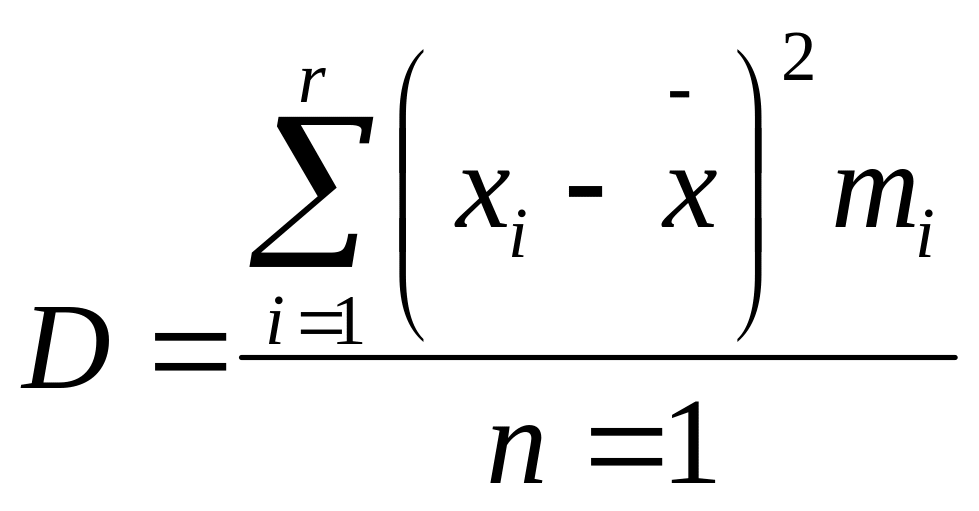(31)

немесе

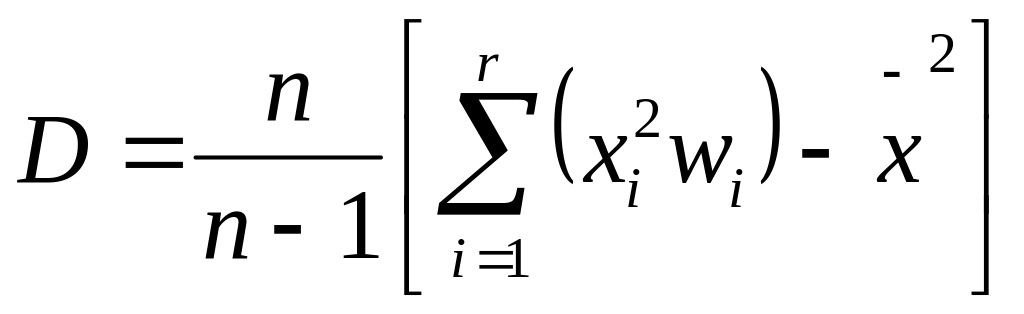(32)

Дисперсия түсінігі – ол белгі өзгергіштігін оның орташа мәнінің вариант ауытқуынан белгілі.

и (33)

Квадратқа келтірілген ауытқу арқылы өзгеру шарты

(34)

- ның орташа квадратты ауытқу мәнінің қатынасы Варияция коэффициенті деп аталады.

(35)

белгісі белгі өзгергіштігін оның мәнімен байланыстырады. өзгергіштік аз, ал - орташа өзгеру, өзгеріс жоғары деп саналады.

НЕГ 1 [78-112 бет], ҚОС 5 [3-15бет]

Бақылау сұрақтары:

1. Басты жиынтық деген не?

2. Аралық варияциалық қатар деген не?

3. Жекелік деген не?

4. Модальды арақашықтықтың негізгі құрамы?

5. Вариациялық қатар қалай анықталады?