Дәріс 9. Тік сызықты тәуелділік моделінің математикалық құрылымы

Теңдеу түрі:

(100)

Тік сызықты теңдеу бар.

а мен в коэффициенті тең екенін көрсетуге болады:

(101)

Онда тік сызықты теңдеудің көрінісі:

_{немесе (102)}

Есептеу үрдісін жеңілдету мақсатында гиперболалық және экспоненциалдық тәуелдік тік сызыққа әкелуді көздейді. Гипербола үшін

(103)

теңдеуді қабылдайды, сонда (тік теңдеу).

(104)

Экспоненті бар болса, сызықтану логорифммен жетеді.

(105)

мен қабылдап, нәтижесінде төмендегі теңдік анықталады.

(106)

Экспонент түрі

(107)

Дәл осылай қала отырып, жаңа өзгермелі қабылдап, нәтижесінде

(108)

Теңдігі орындалады.

Тік сызықты теңдеу дәлдігі

Кез келген тәжірибенің нәтижесі сияқты, регрессия коэффициенттері де кездейсоқ шама болып табылады. Төменде қарастырылған жағдайларда (және олар шындыққа жанасады) үндеулерді бөлу Стьюдент заңына бағынып, еркіндік дәрежесінің санына сай орындалады.

(109)

мұнда: – тәжірибе көлемі;

– регрессия теңдеуінің дәрежесі.

Онда ауытқу кездейсоқ көлем төменгі теңдеумен анықталады.

(110)

мұнда: – орта квадраттық ауытқу

– Стьюдентті бөлу функциясының квантилі.

Кездейсоқ шама аумағының екі жақты тежелуі (минимум мен максимум бойынша).

(111)

Ал шектеудің тек бір жағы қарастырылса (мысалы минимум бойынша), онда

(112)

Ауытқудың шегін сызық регрессияның табамыз. Дәлелдеу бойынша орта квадраттық ауытқу

(113)

мұнда: – былайша айтқанда «қалдық» орта квадраттық ауытқу

(114)

Топтасқан мәліметтер үшін

(115)

Көрсеткіштер мәліметтер бойынша анықталады:

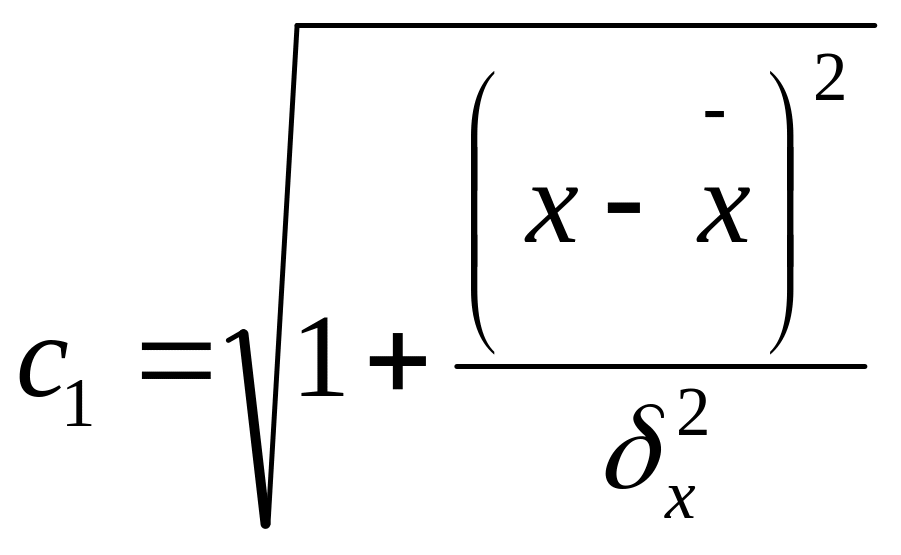(116)

(113) теңдеуден, орта мәнінен х фактор мәнімен анықталады. Ауытқу аймағының шегіне сәйкес кеңеді.

Регрессия теңдеуінің тәжірибесі бойынша мәні «негізгі» қате көлемінің мәнімен бекітіледі. Қате мәнінің максимальді мүмкіндігі төменгі теңдеумен анықталады

(117)

Онда орта квадраттық ауытқу ретінде

(118)

Тәжірибе жүзінде алынған а және в коэффициенттернің мағынасы олардың салыстырмалы түрдегі негізгі мағынасы мына теңдеуде берілген, онда орта квадраттық ауытқу:

(119)

(120)

НЕГ 1 [142-154 бет], ҚОС 6 [12-20 бет]

Бақылау сұрақтары:

1. Тік сызықты теңдеу регрессиясындағы коэффициенттер қалай анықталады?

2. Гиперболалық тәуелділік қалай тізбектеледі?

3. Экспоненциональді тәуелділік қалай тізбектеледі?

4. Үндеулердің жеке мағынасындағы шекті ауытқуларды регрессия сызығындағы ауытқулардан қалай ажыратамыз?

5. «Қалдық» орта квадраттық ауытқу қалай анықталады?