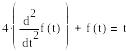Лабораторная работа 7 Численное решение системы дифференциальных уравнений обобщенной электрической машины Теоретическое введение

Математическая модель работы любой электротехнической системы описывается системой дифференциальных уравнений. Для решения систем таких уравнений существуют следующие методы:

1. Метод Эйлера

2. Метод Рунге-Куты

3. Метод обобщенной электрической машины

В данной лабораторной работе мы построим и изучим математическую модель обобщенной электрической машины.

Обобщенная электрическая машина (ОЭМ) представляет собой идеализированную электрическую машину, имеющую две обмотки на статоре и две обмотки на роторе, сдвинутые друг относительно друга на 90 электрических градусов. При таком расположении обмоток количество переменных и уравнений, описывающих электродвигатель, уменьшается, но сохраняется основа электромеханического преобразования энергии - вращающееся магнитное поле. Решение системы уравнений ОЭМ возможно только численными методами.

Электродвигатель может быть представлен в виде электромеханического многополюсника (рис. 7.1):

Рис. 7.1. Электромеханический многополюсник.

Электромеханический преобразователь имеет n-пар электрических выводов, соответствующих n-обмоткам двигателя, и одну пару механических выводов, на которых в результате электромеханического преобразования энергии при скорости ω развивается электромагнитный момент двигателя М.

Как правило, двигатели являются многофазными электрическими машинами. С увеличением числа фаз возрастает число уравнений, описывающих электромагнитные и электромеханические процессы.

В теории электрических машин доказано, что любая многофазная машина с n-фазной обмоткой статора и m-фазной обмоткой ротора может быть представлена двухфазной моделью. Поэтому математическое описание процессов во вращающейся электрической машине получают на основе рассмотрения её двухфазной модели, которая получила название обобщенной электрической машины (рис. 7.2).

Рис. 7.2. Схема обобщенной электрической машины.

Уравнения Кирхгофа, выраженные через потокосцепление Ψ, имеют вид:

Где R₁ и R₂ – активное сопротивление фазы статора и приведённое сопротивление фазы ротора.

В общем виде система дифференциальных уравнений обобщенной электрической машины записывается следующим образом:

где U_su, U_sv, U_ru, U_rv - составляющие векторов напряжений, подводимых к статору и ротору, в осях системы координат u-v, вращающейся с произвольной частотой ω₀; Ψ_su, Ψ_sv, Ψ_ru, Ψ_rv - составляющие векторов потокосцеплений статора и ротора в осях системы координат u-v; ω - круговая частота вращения ротора двигателя; p - число пар полюсов статора; R_s, R_r, L_s’, L_r’, k_s, k_r - активные сопротивления статора, ротора, переходные индуктивности статора и ротора, коэффициенты электромагнитной связи статора и ротора, соответственно; М – электромагнитный момент; J – момент инерции ротора двигателя.

Для вычисления параметров модели обобщенной электрической машины можно воспользоваться формулами:

Для численного решения одиночного дифференциального уравнения в MathCAD имеются функции:

1. Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и сявляется его заключительным ключевым словом. Она решает уравнение методом Рунге-Куты.

Odesolve(x,b,[step]) - Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given. x - переменная интегрирования, действительное число b - конечная точка отрезка интегрирования step - величина шага по переменной интегрирования (необязательный аргумент)

Замечания:

1. Уравнение должно быть линейным относительно старшей производной.

2. Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.

3. При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ' (штрих) - [Ctrl+F7], для знака равенства = [Ctrl+=] (в том числе и для дополнительных условий).

4. Конечная точка должна быть больше начальной.

5. Не допускаются начальные и граничные условия смешанного типа (f '(a)+f(a)=5).

6. Искомая функция в блоке дложна быть обязательно с аргументом ( f(x))

7. Знак производной ставится одновременным нажатием CTRL и F

2. rkfixed(y,x1,x2,n,F) - возвращает матрицу решений системы уравнений методом Рунге-Кутта 4-го порядка при фиксированном шаге по x

решаем систему уравнений сделаем замену х на y0 y на y1

rkadapt(y,x1,x2,n,F) - ищет решение с переменным шагом ( там, где решение меняется медленнее, шаг увеличивается, а в области быстрого изменения решения шаг функции уменьшается). Возвращается решение с равным шагом. Функция работает быстрее, чем rkfixed

Bulstoer(y,x1,x2,n,F) - дает более точное решение (методом Bulirsch-Stoer)

Агрументы вышеуказанных функций:

y - вектор начальных условий

x1,x2 - границы интервала для поиска решения

n - количество точек на интервале

F(x,y) - вектор-функция первых производных

При решении дифференциальных уравнений порядка выше первого (или систем уравнений, выше первого порядка) исходное уравнение (систему) необходимо преобразовать к системе дифференциальных уравнений первого порядка.

В результате работы укзанных функций рассчитывается матрица, количество стобцов которой равно порядку уравнения +1(или сумме порядков уравнений в системе +1), а количество строк равно параметру n. Первый столбец содержит значения независимой переменной, второй - значение функции, третий - для диф. уравнений 2-го порядка - значение производной искомой функции (если решается система двух уравнений 1-го порядка, то третий столбец будет содержать значения второй функции). Для выделения решений (функций или их производных) можно воспользоваться стандартным оператором вывода столбцов матрицы M^{< >}

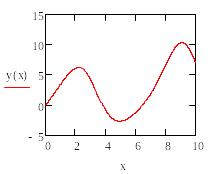
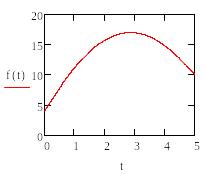
В следующем примере решаем систему диф. уравнений второго порядка:

 

Если матрица правых частей дифференциальных уравнений почти вырождена, то такие системы называются жесткими. В этом случае решения, возвращаемые функцией rkfixed будет неустойчивым и для решения таких систем необходимо применять функции Stiffb , Stiffr

3. Stiffb(y,x1,x2,n,F,J) - ищет решение диф. уравнения или системы дифференциальных уравнений методом Bulirsch-Stoer

Stiffr(y,x1,x2,n,F,J) - ищет решение диф. уравнения или системы дифференциальных уравнений методом Rosenbrock

Первые пять аргументов такие же,как и при решении хорошо обусловленных систем дифференциальных уравнений . Дополнительный аргумент - матрица Jразмером nx(n+1), первый столбец которой содержит частные производные dF/dx, остальные столбцы и строки представляют собой матрицу Якоби dF/dy

4. Для отыскания решения системы диф. уравнений только в конечной точке используются функции bulstoer,rkadapt, stiffb, stiffr (начинаются с прописной буквы).

Набор парамеров для этих функций: bulstoer(y,x1,x2,acc,F,kmax,save)  rkadapt(y,x1,x2,acc,F,kmax,save)  stiffb(y,x1,x2,acc,F,J,kmax,save)  stiffr(y,x1,x2,acc,F,J,kmax,save)

Первые три параметра и пятый (F) этих функций те же, что и для функции Rkadapt.

Дополнительные параметры:

acc - параметр, контролирующий точность решения (реком. асс=0.001) 

kmax - максимальное число промежуточных точек в которых ищется решение 

save - минимально допустимый интервал между точками, в которых ищется решение

Задание на лабораторную работу:

Согласно варианту записать систему дифференциальных уравнений и решить её ВСЕМИ способами в mathcad. Параметры двигателей приведены в таблице 7.1 Двигатели асинхронные с короткозамкнутым ротором, поэтому U_ru = U_rv = U_sv = 0, U_su = U_ном, ω_k = 314 (рад/с).

Параметры двигателей

Табл. 7.1

вариант	Тип двигателя	Rs, Ом	Rr’, Ом	xs, Ом	xm, Ом	xr’, Ом	Uном, В	p	J, кг*м2
1	4A80A4Y3	7,3	5	142	136	145	220	2	0,0032
2	4AK160S4Y3	0,346	0,479	28	27	28	220	2	0,1
3	ВРП160М4	0,536	0,406	36	35	36	380	2	0,175
4	2АЗМУХЛ4	0,622	6,4	152	58	98	220	2	18,25
5	4A100L8УЗ	0,725	5	69	23	142	380	2	22,5
6	4A100LбУЗ	8,2	0,346	58	69	58	6000	4	22,5
7	4A112МА6УЗ	0,479	7,3	140	114	140	6000	4	38,3
8	4A112МА8УЗ	0,479	0,346	145	135	28	6000	4	45
9	4A132М6УЗ	0,406	0,536	28	98	36	6000	4	4
10	4A132М8УЗ	0,536	3,71	36	142	152	6000	4	100
11	4A160S8УЗ	0,406	2,65	129	28	64	6000	4	4,5
12	4A160М6УЗ	0,958	1,25	142	36	82	6000	4	117,5
13	4A160М8УЗ	0,479	0,479	28	152	36	6000	4	5
14	4A180М6УЗ	6,4	0,406	23	69	145	6000	4	135
15	4A200L8УЗ	5	0,536	69	58	28	6000	4	8,75
16	4A200LбУЗ	0,346	0,622	114	140	36	6000	4	11,25
17	4A200М6УЗ	0,536	0,725	135	35	129	6000	4	12
18	АТД4	0,536	8,2	98	58	142	380	2	1,25
19	2АДО-С	0,479	0,479	142	23	28	380	1	8,3
20	2АДОТ	0,406	7,3	28	23	36	380	1	4,26
21	4А3МВ1	0,536	0,406	36	69	152	380	2	5,2
22	2А3МВ1	0,536	0,346	152	114	69	380	2	7,45
23	1А3МВ	0,479	0,536	64	135	58	380	2	9,1
24	АВЗВ	7,3	5	82	98	140	380	6	2,29
25	ВАОКЭ	0,479	0,406	36	142	74	380	6	3,15

Контрольные вопросы

1. Методы численного решения дифференциальных уравнений.

2. Расскажите о методах Рунге-Кутты.

3. Применение метода Эйлера к решению дифференциальных уравнений.

4. Применение конечно-разностных методов к решению систем дифференциальных уравнений.

5. Какие формы записи систем дифференциальных уравнений вы знаете?

6. Применение метода Рунге-Кутты четвертого порядка к решению систем дифференциальных уравнений в форме Коши.

7. Что вы знаете об обобщенной электрической машине?

8. Допущения, принимаемые в теории обобщенной электрической машины.

9. Система уравнений обобщенной электрической машины.

10. Какие методы повышения точности интегрирования вы знаете?

11. Расскажите о применении метода Рунге-Кутты четвертого порядка с адаптивным шагом к численному решению системы дифференциальных уравнений обобщенной электрической машины.